决策树

概述

? 树模型

　　? 从根节点一步一步走到叶子节点 ( 决策 )

　　? 所有数据都会落在叶子节点, 既可以做分类也可以做回归

? 树的组成

　　? 根节点  -  第一个选择点

　　? 非叶子节点与分支  -   中间过程

　　? 叶子节点 -  最终的决策结果

? 节点

　　? 节点相当于在数据中进行切一刀 ( 切分两部分 -  左右子树 )

　　? 节点越多越好吗?  -  

? 决策树的训练和测试

　　? 训练阶段  -  从给定的训练集构造一棵树 ( 从根节开始选择特征, 如何进行特征切分 )

　　? 测试阶段  -  根据构造出来的树模型从上到下走一遍

　　? 难点  -  测试阶段较为容易, 而训练阶段并不简单

? 如何切分特征 ( 选择节点 )

　　? 问题  -  一个数据集中可能存在多个特征的时候, 选择那个节点特征作为根节点进行分支, 以及其他特征分支的选择顺序都是问题

　　? 目标 - 需要通过一种衡量标准, 来计算不同特征进行分支选择后的分类情况, 找出最好的那个当做根节点, 以此类推

决策树算法 - 信息增益

? 衡量标准 - 熵

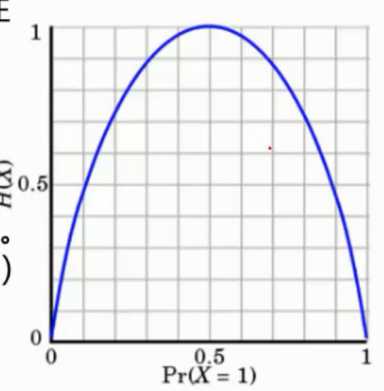
　　? 熵  -  表示随机变量的不确定性的度量  ( 简单来说就是混乱程度 )

　　　　当 p = 0 或者 p = 1 的时候， H(p) = 0, 随机变量完全没有不确定性

　　　　当 p = 0.5 时， H(p) = 1 此时，随机变量的不确定性最大

　　? 公式  -  

　　? 栗子  -   a = [1,1,1,2,1,2,1,1,1] ,  b = [1,5,6,7,5,1,6,9,8,4,5]    a 的熵更底, 因为 a 的类别较少, 相对 b 就更稳定一些

　　? 信息增益  -  表示特征 X 使 Y 的不确定性减少的程度 （分类后的专一性， 希望分类后的结果同类在一起）

? 示例

? 数据  -  14 天打球情况

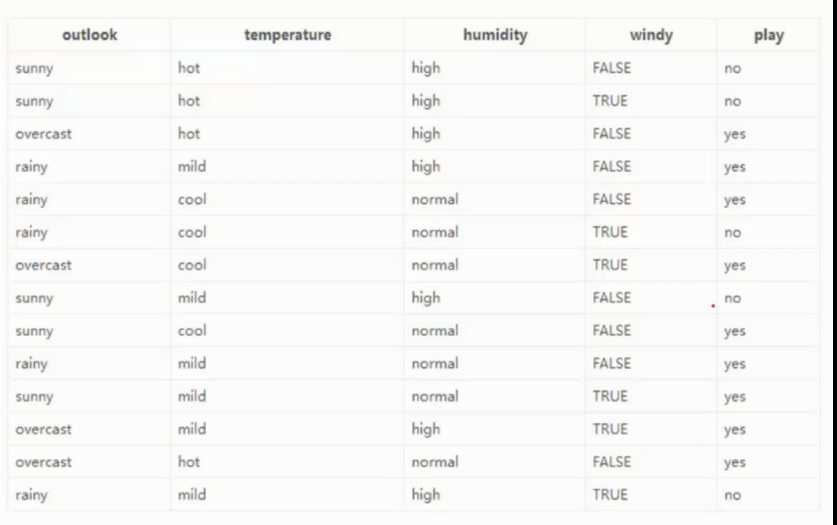
? 特征  -  4 种天气因素  

?目标  - 构建决策树

? 根节点选择

　　14天的记录中, 有 9 天打球, 5 天没打球, 熵为 

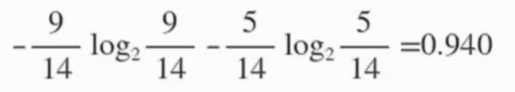
　　演示 -  outlook 特征 - 天气

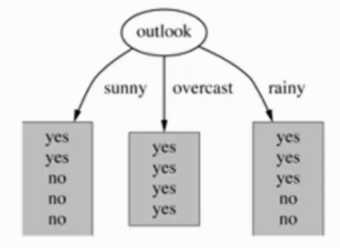
　　suuny 的概率是 5/14 , 熵 是 0.971 　　

　　overcast 的概率是 4/14 , 熵 是 0 　

　　rainy 的概率是 5/14 , 熵 是 0.971 　

　　熵值计算 :  5/14*0.971 + 4/14*0 + 5/14*0.971 = 0.693

　　信息增益 :  系统的 熵值从原始的 0.940 下降到了 0.693 , 增益为 0.247

　　以此类推进行处理, 选出根节点然后再从剩余的特征中选择次根节点往下到仅剩最后一个特征, 

? 总结

? 弊端

　　如 id 这样的唯一标识特征列, 会让熵值计算为 0 被视为最大信息增益 ,

　　 但是 id 仅仅是编号标识对信息的模型无任何影响实则无效项

? 解决 

　　 信息增益率   -   解决信息增益问题,  考虑自身熵 

　　 GINI 系数  -     ( 和熵的衡量标准类似, 计算方式不同 )

特殊处理

? 连续值处理

本质上就上 离散化

对序列遍历然后寻找离散点进行二分

? 剪枝策略

? 为毛 

　　决策树拟合风险过大, 理论上可以完全分开数据, 让每个叶子节点都只有一个命中数据

　　训练集中的数据这样完美命中, 但是在测试集中可能会出现不适配等各种异常情况

? 策略

　　预剪枝 - 边简历决策树边进行剪枝操作 ( 更实用 ) 

　　后剪枝 - 当建立完决策树后进行剪枝操作

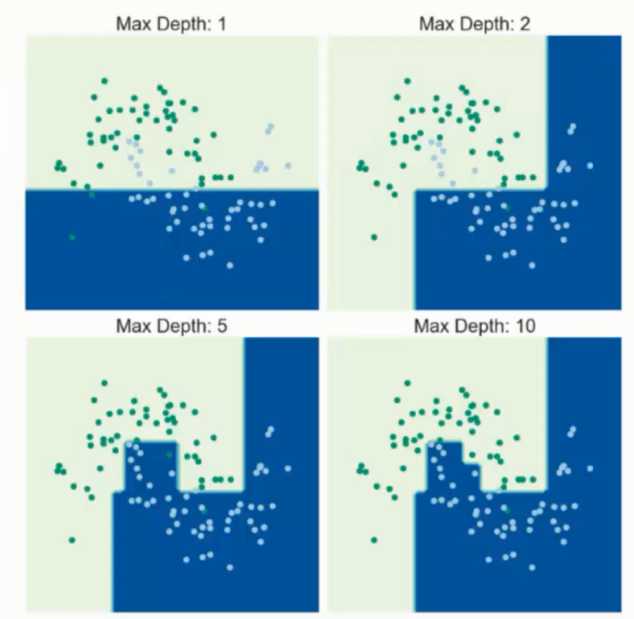
? 预剪枝

 　　限制 深度,  叶子节点个数, 叶子节点样本数, 信息增益量等

? 后剪枝

 　　通过一定的衡量标准 - 叶子越多, 损失 (C(T)) 越大

代码

决策树

原文：https://www.cnblogs.com/shijieli/p/11534183.html