其实二叉平衡树就是通过各种奇异的操作从而维持二叉树的平衡
fhq Treap特殊就特殊在它并没有像其他性能非常优越的平衡二叉树一样是通过旋转从而实现二叉树的平衡
fhq Treap的核心操作其实就两个 ---- 分裂 和 合并
分裂就是把一棵二叉平衡树 分成两个二叉平衡树, 左边的二叉平衡树的所有点的权值都 < 右边二叉平衡树所有点的权值
分裂的方式有两种 :
1、 按值分裂
2、按排名分裂
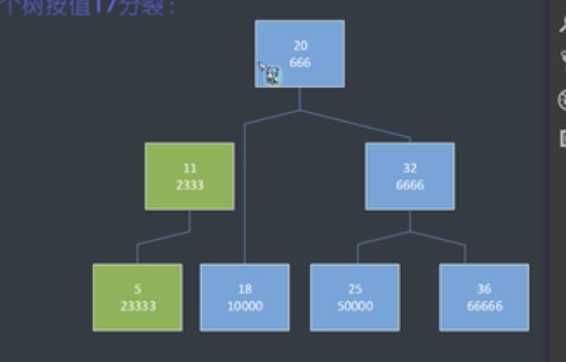
这里先讲按值分裂:
如果我们遍历到的当前这个结点的值 <= val ,那么我们就把这个结点放入左边的树 。
如果当前这个结点的值 > val , 那么我们就把这个结点放入右边的树
这里采用传入引用的写法更为简单,x 和 y分别代表分裂出来的两个树的根结点
1 void split(int now,int val,int &x,int &y){ 2 if (!now) 3 x = y = 0; 4 else { 5 if (fhq[now].val <= val ) { 6 x = now; 7 split(fhq[now].r,val,fhq[now].r,y); 8 } 9 else { 10 y = now; 11 split(fhq[now].l,val,x,fhq[now].l); 12 } 13 update(now); 14 } 15 }
合并的话 我们要严格保证x < y
并且我们规定了 父亲结点优先级 > 孩子结点的优先级
1 int merge(int x,int y) { 2 if (!x || !y) 3 return x+y; 4 if (fhq[x].key > fhq[y].key) { 5 fhq[x].r = merge(fhq[x].r,y); 6 update(x); 7 return x; 8 } 9 else { 10 fhq[y].l = merge(x,fhq[y].l); 11 update(y); 12 return y; 13 } 14 }
删除:
假设我们要删除权值为 val 的这个结点
那么我们首先把树 分成 <= val 和 > val 的两棵树 x 和 z
然后我们再把 x 这个树分为 <= val-1 和 == val 的两棵树 x 和 y
然后我们在把 y 这个树的根结点去掉就好了。
最后合并 x 和 y ,再和 z
1 void del(int val) { 2 split(root,val,x,z); 3 split(x,val-1,x,y); 4 y = merge(fhq[y].l,fhq[y].r); 5 root = merge(merge(x,y),z); 6 }
求前驱、后继
求x的前驱的定义是: 小于x的最大的数
那么我们可以把树分成两棵 : 一棵 <= val-1 另一棵 > val -1 ,因为是找最大的数所以我们不断的遍历x这个树的右子树就可以了
求x的后继的定义是: 大于x的最小的数
那么我们可以把树分成两棵: 一棵 <= val 另一棵 > val ,因为我们是最小的数 所以我们不断的遍历y这个树的左子树就可以了
求排第几名、排第几名的数是哪个
直接看代码就好了,思想也非常的简单
完整模版代码:
1 #include <stdio.h> 2 #include <iostream> 3 #include <string.h> 4 #include <random> 5 6 const int maxn = 1e5 + 10; 7 8 struct Node { 9 int l,r; 10 int val,key; 11 int size; 12 }fhq[maxn]; 13 14 int cnt,root; 15 16 std::mt19937 rnd(233); 17 18 int newnode(int val){ 19 fhq[++cnt].val = val; 20 fhq[cnt].key = rnd(); 21 fhq[cnt].size = 1; 22 return cnt; 23 } 24 25 void update(int now){ 26 fhq[now].size = fhq[fhq[now].l].size + fhq[fhq[now].r].size + 1; 27 } 28 29 void split(int now,int val,int &x,int &y){ 30 if (!now) 31 x = y = 0; 32 else { 33 if (fhq[now].val <= val ) { 34 x = now; 35 split(fhq[now].r,val,fhq[now].r,y); 36 } 37 else { 38 y = now; 39 split(fhq[now].l,val,x,fhq[now].l); 40 } 41 update(now); 42 } 43 } 44 45 int merge(int x,int y) { 46 if (!x || !y) 47 return x+y; 48 if (fhq[x].key > fhq[y].key) { 49 fhq[x].r = merge(fhq[x].r,y); 50 update(x); 51 return x; 52 } 53 else { 54 fhq[y].l = merge(x,fhq[y].l); 55 update(y); 56 return y; 57 } 58 } 59 60 int x,y,z; 61 62 void ins(int val) { 63 split(root,val,x,y); 64 root = merge(merge(x,newnode(val)),y); 65 } 66 67 void del(int val) { 68 split(root,val,x,z); 69 split(x,val-1,x,y); 70 y = merge(fhq[y].l,fhq[y].r); 71 root = merge(merge(x,y),z); 72 } 73 74 void getrank(int val) { 75 split(root,val-1,x,y); 76 printf("%d\n",fhq[x].size + 1); 77 root = merge(x,y); 78 } 79 80 void getnum(int rank) { 81 int now = root; 82 while (now) { 83 if (fhq[fhq[now].l].size + 1 == rank) 84 break; 85 else if (fhq[fhq[now].l].size >= rank){ 86 now = fhq[now].l; 87 } 88 else { 89 rank -= fhq[fhq[now].l].size + 1; 90 now = fhq[now].r; 91 } 92 } 93 printf("%d\n",fhq[now].val); 94 } 95 96 void pre(int val) { 97 split(root,val-1,x,y); 98 int now = x; 99 while (fhq[now].r) 100 now = fhq[now].r; 101 printf("%d\n",fhq[now].val); 102 root = merge(x,y); 103 } 104 105 void nxt(int val) { 106 split(root,val,x,y); 107 int now = y; 108 while (fhq[now].l) 109 now = fhq[now].l; 110 printf("%d\n",fhq[now].val); 111 root = merge(x,y); 112 } 113 114 int main() { 115 int t; 116 scanf("%d",&t); 117 while (t--) { 118 int opt,val; 119 scanf("%d%d",&opt,&val); 120 switch (opt) { 121 case 1: 122 ins(val); 123 break; 124 case 2: 125 del(val); 126 break; 127 case 3: 128 getrank(val); 129 break; 130 case 4: 131 getnum(val); 132 break; 133 case 5: 134 pre(val); 135 break; 136 case 6: 137 nxt(val); 138 break; 139 } 140 } 141 return 0; 142 }
原文:https://www.cnblogs.com/-Ackerman/p/11537567.html