Chrod算法是P2P中的四大算法之一,是有MIT(麻省理工学院)于2001年提出,其他三大算法分别是:
Chord的目的是提供一种能在P2P网络快速定位资源的的算法,Cord并不关心资源是如何存储的,只是从算法层面研究资源的取得,因此Chord的API就简单到只有一个set、get。
Chord是一个算法,也是一个协议。作为一个算法,Chord可以从数学的角度严格证明其正确性和收敛性;作为一个协议,Chord详细定义了每个环节的消息类型。当然,Chord之所以受追捧,还有一个主要原因就是Chord足够简单,3000行的代码就足以实现一个完整的Chord。
Chord还可以被作为一个一致性哈希、分布式哈希(DHT)的实现。
覆盖网络是指这样一种网络:构建在其他网络之上、网络节点之间通过虚拟或逻辑连接在一起,比如云计算、分布式系统都是覆盖网络,因为其都构建于TCP/IP之上,且节点之间有联系。Chord也是构建于覆盖网络。
非结构化的P2P网络是指网络节点之间不存在组织关系,节点之间完全是对等的,比如第一代P2P网络Napster,这类网络结构清晰、简单,但查找没有多大的优化余地,经常采用全局或分区泛洪查找,查找时间长、且结果难以保证(有可能在找到前就超时)。
结构化的P2P网络与非结构化恰好相反,我们认为网络在逻辑上存在一个人为设计的结构,比如Chord假定网络是一个环,Kadelima则假定为一颗二叉树,所有的节点均为树的叶子节点。有了这些逻辑结构,就给我们资源查找引入了更多的算法和思路。
DHT的主要想法是把网络上资源的存取像Hashtable一样,可以简单而快速地进行put、get,该思想的诞生主要是受第一代P2P(Napster)网络的影响。与一致性哈希相比,DHT更强调的是资源的存取,而不管资源是否是一致性的。与一致性哈希相同的是,DHT也只是一个概念,具体细节留给各实现。
当前这些P2P实现可以被作为DHT的具体实现,再次再列举一些有代表性的实现:
Chord通过把Node和Key映射到相同的空间而保证一致性哈希,为了保证哈希的非重复性,Chord选择SHA-1作为哈希函数,SHA-1会产生一个2160的空间,每项为一个16字节(160bit)的大整数。我们可以认为这些整数首尾相连形成一个环,称之为Chord环。整数在Chord环上按大小顺时针排列,Node(机器的IP地址和Port)与Key(资源标识)都被哈希到Chord环上,这样我们就假定了整个P2P网络的状态为一个虚拟的环,因此我们说Chord是结构化的P2P网络。
下面有几个定义:
如图:
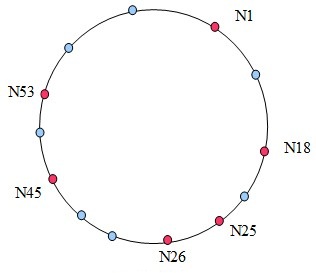
红色点为Node,蓝色为标志符。上面只是部分节点和标志符,以节点N1为例说明其Finger表中的successor:
| No | ith successor | Successor |
| 1 | N1+20 | N18 |
| 2 | N1+21 | N18 |
| 3 | N1+22 | N18 |
| 4 | N1+23 | N18 |
| 5 | N1+24 | N18 |
| 6 | N1+25 | N45 |
| 7 | N1+26 | N1 |
| 8 | N1+27 | N1 |
把Node和Key都映射到一个值域感觉是把狗和猫放在一起衡量,虽然有点怪,但这样可以保证一致性哈希,具体可以参考前文。
很显然,分布在Chord环上的Node数远远小于标志符数(2160是一个无法衡量的天文数字),这样Chord环上的Node就会很稀疏地分布在Chord环上,理论上应该是随机分布,但如前面一致性哈希的讨论,如果节点数量不多,分布肯定是不均匀的,可以考虑增加虚拟节点来增加其平衡性,如果在节点较多(比如大型的P2P网络有上百万的机器)就不必引入虚拟节点。
很显然,任何查找只要沿Chord环一圈结果肯定可以找到,这样的时间复杂度是O(N),N为网络节点数,但对一个上百万节点,且节点经常加入、退出的P2P网络来说,O(N)是不可忍受的,因此Chord提出了下面非线性查找的算法:
从直觉上来说,上次查找过程应该是指数收敛的,类似二分法的查找,收敛速度应该是很快的;反过来,查找时间或路由复杂度应该是对数即的,在下面我们会证明这一点。
下图表明了节点N1查找节点N53的过程,还是非常快的:
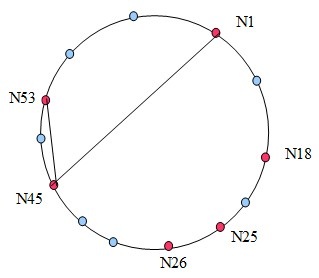
对一个算法而言,收敛性是至关重要的,如果没有收敛性做保证,在程序上化再多的心思也是徒劳。在证明之前,我们再强调3点:
这里要区分是Key的successor还是节点n的successor,同时要注意最近匹配原则。
假如节点n的Finger表中的第i个successor与Key的距离最近,则满足:Key处在第i项与第i+1项中间
记第i项为J,第i+1项为P
而:
J = n + 2i-1
P = n + 2i
节点n与Key的距离应该处在n与J和P的中间,即 J-n<n - hash(Key)<P - n
(1) 2i-1<n - hash(Key)<2i
(2) 而J与Key的距离最大为J与P的距离 J-hash(Key) <P - J = 2i-1
也就是说J与Key的距离,小于n与Key的距离,并且该距离小于n与Key距离的一半,这样我们保证每次迭代,与Key的距离都会收敛,并且至少按2的指数收敛,也就是折半查找。
至此,我们理论证明了Chord的收敛性。
其实Chord算法可以完全转换为一个数学问题:
在Chord环上任意标记个点作为Node集合,任意指定Node T,从任意的Node N开始根据Chord查找算法都能找到节点T。
为什么能这么转换呢?因为只要找到了Key的直接前继,也就算找到了Key,所有问题转化为一个在Chord环上通过Node找Node的问题。这样,这个题就马上变的很神奇,假如我们把查找的步骤记录为路径,又转化为任意2个节点之间存在一条最短路径,而Chord算法其实就是构造了这样一条最短路径,那这样的路径会不会不存在呢?不会的,因为Chord本身是一个环,最差情况可以通过线性查找保证其收敛性。
从最短路径的角度来看,Chord只是对已存在线性路径的改进,根据这个思路,我们完全可以设计出其他的最短路径算法。从算法本来来看,保证算法收敛或正确性的前提是每个Node要正确地维护其后继节点,但在一个大型的P2P网络中,会有节点的频繁加入、退出,如果没有额外的工作,很难保证每个节点有正确的后继。
Chord冗余性:
所谓冗余性是指Chord的Finger表中存在无用项,那些处在Node N和其successor之间的项均无意义,因为这些项所代表的successor不存在。比如在N1的Finger表中的第1~5项均不存在,故都指向了N18,至少第1~4项为冗余信息。
一般说来,假如Chord环的大小为2m,节点数为2n,假如节点平均分布在Chord环上,则任一节点N的Finger表中的第i项为冗余的条件为:N+2i-1<N + 2m/2n =>2i-1<2m-n =>i <m-n+1,即当i <m-n+1时才有冗余。
冗余度为:(m-n+1)/m=1-(n-1)/m,一般说来m >>n,所以Chord会存在很多的冗余信息。假如,网络上有1024个节点,即n=10,则冗余度为:1-(10-1)/160≈94%。所以很多论文都指出这一点,并认为会造成冗余查询,降低性能。其实不然,因为这些冗余信息是分布在多个Node的Finger表,如果采取适当的路由算法,对路由计算不会有任何影响。
至此,我们已经完整地讨论了Chord算法及其核心思想,接下来要讨论的是Chord的具体实施。
转载 http://blog.csdn.net/chen77716/article/details/6059575
原文:http://www.cnblogs.com/chenying99/p/3920973.html