写在前面:
一:排序算法的分类:
1.内部排序和外部排序
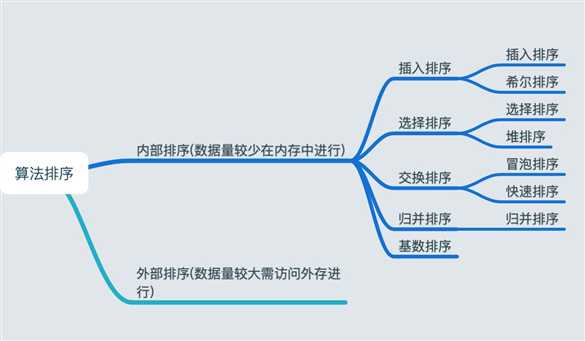
2.比较类排序和非比较排序
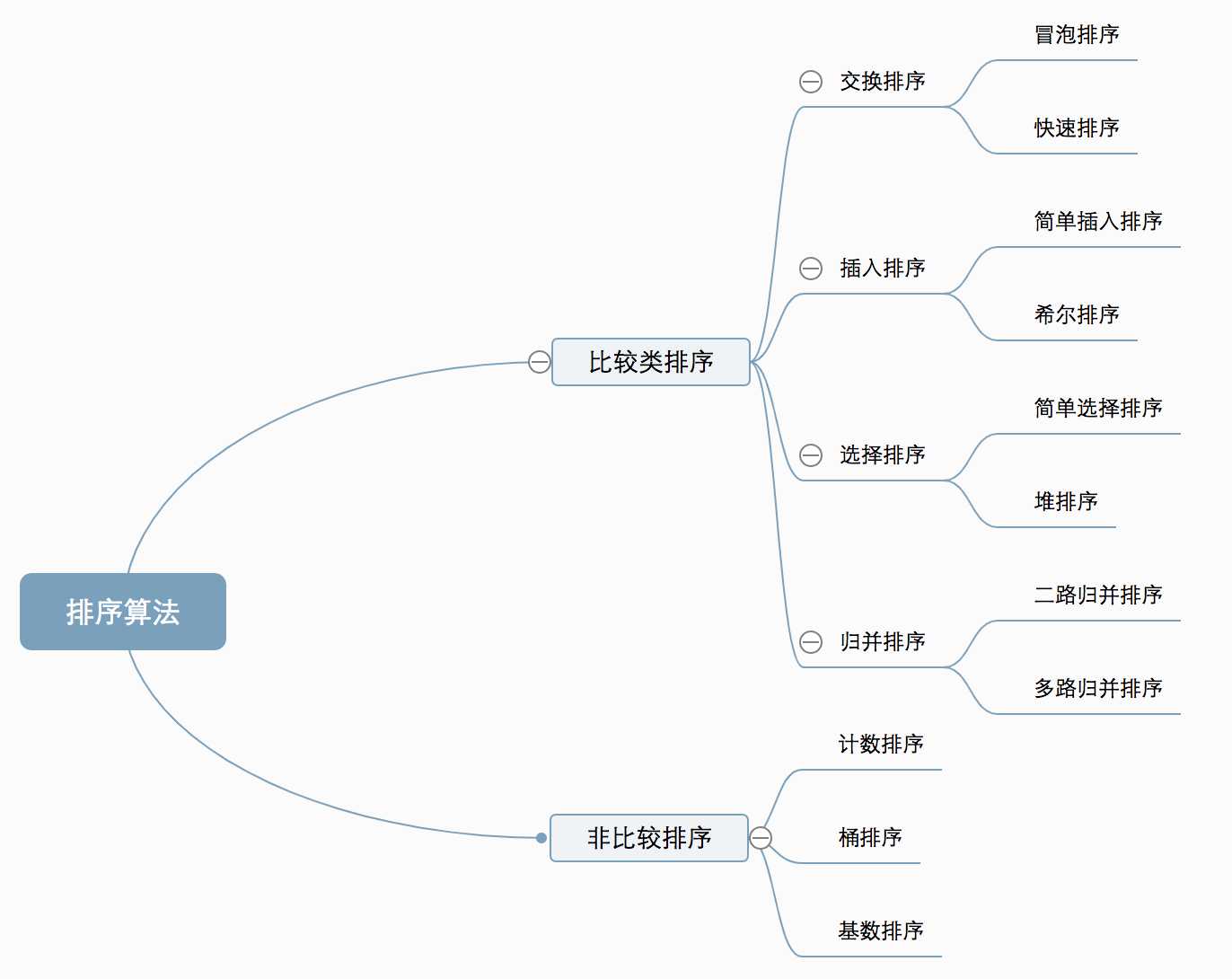
二、复杂度分析,算法稳定性和适用场景
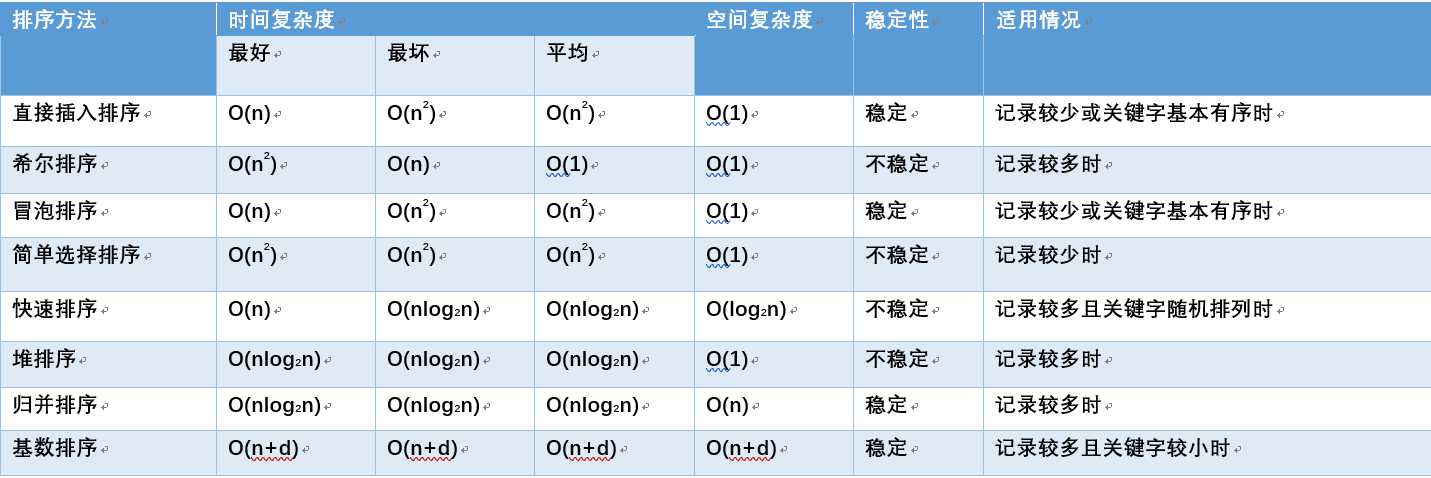
排序算法第一弹:简单的冒泡,选择和插入排序
网上关于排序算法的文章有很多,代码示例也有很多,但质量可以说是良莠不齐,有的艰涩难懂,有的代码冗余优化不够,甚至还有错的(在学习快排时就曾经盯着一个错误的代码示例揣摩了一个多小时,气死我了)我在下面所给出的代码示例都是经过系列学习自己敲打出来的,应该是比较简单易懂,逻辑清晰没有什么不周之处,应该比较适合初学者学习借鉴。至少目前自己还感觉良好,如果读者发现有什么需要改进优化的地方欢迎在评论区评论斧正!
我是想将这几种常见的排序算法做成一个工具包的,所以每一个排序算法类中的排序方法都用static关键字修饰并将排序好的数组作为返回值返回。每个算法类中也有简单main方法用于测试算法。
冒泡排序:
模拟排序图解:
整体效果:
排序过程细节:
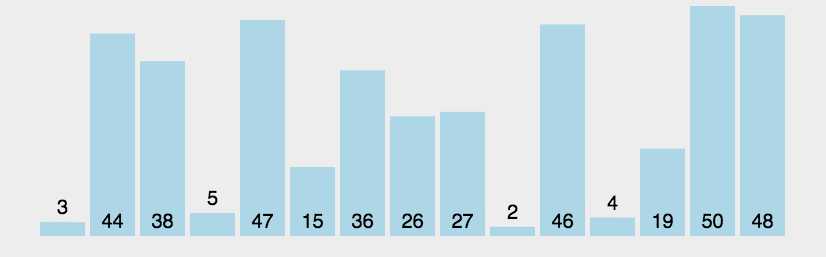
排序原理:
我的代码实现:
1 package cn.ftf.mysort;
2
3 import java.util.Arrays;
4
5 public class MyBubbleSort {
6 public static int[] bubbleSort(int[] arr) {
7 int temp;
8 int flag;
9 for(int i=1;i<arr.length;i++) {
10 flag=0;
11 for(int j=0;j<arr.length-i;j++) {
12 if(arr[j]>arr[j+1]) {
13 flag=1;
14 temp=arr[j];
15 arr[j]=arr[j+1];
16 arr[j+1]=temp;
17 }
18 }
19 if(flag==0) {
20 break;
21 }
22 flag=0;
23 }
24 return arr;
25 }
26 public static void main(String[] args) {
27 int [] arr= {1,7,8,9,12,2,6,10,14,18,1};
28 arr=bubbleSort(arr);
29 System.out.println(Arrays.toString(arr));
30 }
31 }
复杂度分析:
1. 不管原始数组是否有序,时间复杂度都是O(n2)。
因为没一个数都要与其他数比较一次,(n-1)2次,分解:n2+2n-1, 去掉低次幂和常数,剩下n2,所以最后的时间复杂度是n2
2. 空间复杂度是O(1),因为只定义了一个辅助变量,与n的大小无关,所以空间复杂度为O(1)
选择排序:
模拟排序图解:
整体效果:
排序过程细节:
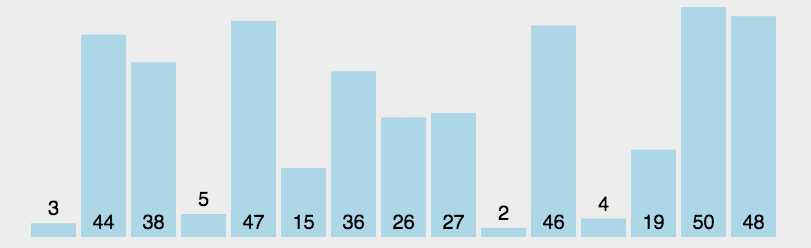
排序原理:
1. 第一个跟后面的所有数相比,如果小于(或小于)第一个数的时候,暂存较小数的下标,第一趟结束后,将第一个数,与暂存的那个最小数进行交换,第一个数就是最小(或最大的数)
2. 下标移到第二位,第二个数跟后面的所有数相比,一趟下来,确定第二小(或第二大)的数,重复以上步骤,直到指针移到倒数第二位,确定倒数第二小(或倒数第二大)的数,那么最后一位也就确定了,排序完成。
我的代码实现:
1 package cn.ftf.mysort;
2
3 import java.util.Arrays;
4
5 public class MyChooseSort {
6 public static int[] chooseSort(int[]arr) {
7 int temp=0;
8 for(int i=0;i<arr.length-1;i++) {
9 for(int j=i+1;j<arr.length;j++) {
10 if(arr[i]>arr[j]) {
11 temp=arr[i];
12 arr[i]=arr[j];
13 arr[j]=temp;
14 }
15 }
16 }
17 return arr;
18 }
19 public static void main(String[] args) {
20 int [] arr= {1,7,8,9,12,2,6,10,14,18};
21 arr=chooseSort(arr);
22 System.out.println(Arrays.toString(arr));
23 }
24
25 }
复杂度分析:
1. 不管原始数组是否有序,时间复杂度都是O(n2),
因为没一个数都要与其他数比较一次,(n-1)2次,分解:n2-2n+1, 去掉低次幂和常数,剩下n2,所以最后的时间复杂度是n2
2. 空间复杂度是O(1),因为只定义了两个辅助变量,与n的大小无关,所以空间复杂度为O(1)
直接插入排序:
模拟排序图解:
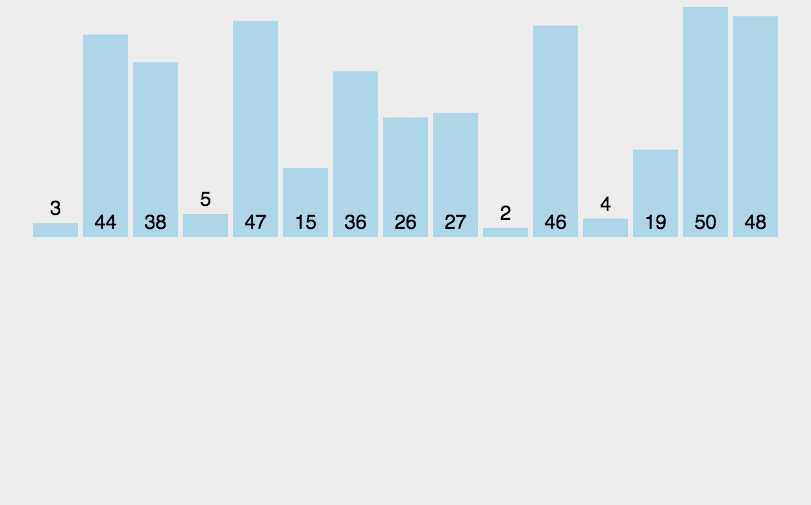
排序原理:
1. 从第二位开始遍历,
2. 当前数(第一趟是第二位数)与前面的数依次比较,如果前面的数大于当前数,则将这个数放在当前数的位置上,当前数的下标-1。
3. 重复以上步骤,直到当前数不大于前面的某一个数为止,这时,将当前数,放到这个位置,1-3步就是保证当前数的前面的数都是有序的,内层循环的目的就是将当前数插入到前面的有序序列里。
4. 重复以上3步,直到遍历到最后一位数,并将最后一位数插入到合适的位置,插入排序结束。
我的代码实现:
1 package cn.ftf.mysort;
2 /*
3 * 我的插入排序
4 */
5 import java.util.Arrays;
6
7 public class MyInserSort {
8 public static int[] inserSort(int[] arr) {
9 for(int i=1;i<arr.length;i++) {
10 int inserValue=arr[i];
11 int inserIndex=i-1;
12 while(inserIndex>=0&&inserValue<arr[inserIndex]) {
13 arr[inserIndex+1]=arr[inserIndex];
14 inserIndex--;
15 }
16 if(inserIndex!=i)
17 arr[inserIndex+1]=inserValue;
18 }
19 return arr;
20 }
21 public static void main(String[] args) {
22 int[] arr= {3,23,3,456,99,2,1,-12,-3,1,6,9,7};
23 arr=inserSort(arr);
24 System.out.println(Arrays.toString(arr));
25 }
26 }
复杂度分析:
1. 时间复杂度:插入算法,就是保证前面的序列是有序的,只需要把当前数插入前面的某一个位置即可。
所以如果数组本来就是有序的,则数组的最好情况下时间复杂度为O(n)
如果数组恰好是倒=倒序,比如原始数组是5 4 3 2 1,想要排成从小到大,则每一趟前面的数都要往后移,一共要执行n-1 + n-2 + … + 2 + 1 = n * (n-1) / 2 = 0.5 * n2 - 0.5 * n次,去掉低次幂及系数,所以最坏情况下时间复杂度为O(n2)
平均时间复杂度(n+n2 )/2,所以平均时间复杂度为O(n2)
2. 空间复杂度:插入排序算法,只需要两个变量暂存当前数,以及下标,与n的大小无关,所以空间复杂度为:O(1)
三种排序算法的排序速度测试:
生成一个包含80000个随机数的数组,测试三种算法完成排序所用的时间。
1 import cn.ftf.mysort.MyBubbleSort; 2 import cn.ftf.mysort.MyChooseSort; 3 import cn.ftf.mysort.MyInserSort; 4 5 /* 6 * 我的排序算法速度测试 7 */ 8 public class MySortText { 9 public static void main(String[] args) { 10 int[] arr; 11 arr = new int[80000]; 12 for(int i =0; i < 80000;i++) { 13 arr[i] = (int)(Math.random() * 10000); 14 } 15 long firstTime=0; 16 long secondTime=0; 17 18 firstTime=System.currentTimeMillis(); 19 MyBubbleSort.bubbleSort(arr); 20 secondTime=System.currentTimeMillis(); 21 System.out.println("冒泡排序用时:"+(secondTime-firstTime)); 22 23 arr = new int[80000]; 24 for(int i =0; i < 80000;i++) { 25 arr[i] = (int)(Math.random() * 10000); 26 } 27 firstTime=System.currentTimeMillis(); 28 MyChooseSort.chooseSort(arr); 29 secondTime=System.currentTimeMillis(); 30 System.out.println("选择排序用时:"+(secondTime-firstTime)); 31 32 arr = new int[80000]; 33 for(int i =0; i < 80000;i++) { 34 arr[i] = (int)(Math.random() * 10000); 35 } 36 firstTime=System.currentTimeMillis(); 37 MyInserSort.inserSort(arr); 38 secondTime=System.currentTimeMillis(); 39 System.out.println("直接插入排序用时:"+(secondTime-firstTime)); 40 } 41 }
生成测试结果:
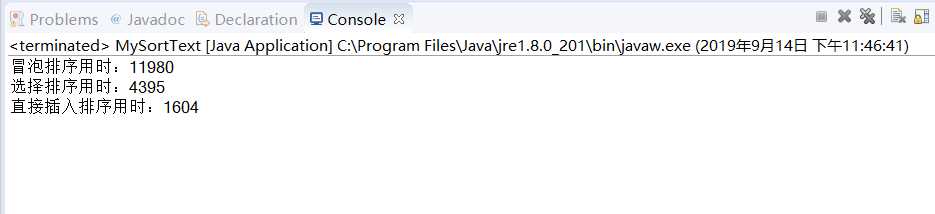
可见这三种排序算法在排序大量级的数据时速度差距还是很大的,同样排80000个数,冒泡排序用时将近12s ,选择排序用时4.4s ,直接插入排序用时1.6s 。
三种排序算法的使用情景:
若n较小(如n≤50),可采用直接插入或直接选择排序;
当记录规模较小时,直接插入排序较好;如果直接选择移动的记录数少于直接插人,应选直接选择排序为宜;
若文件初始状态基本有序(指正序),则应选用直接插人、冒泡或随机的快速排序为宜;
还需要注意的是,这三种排序算法,冒泡排序和直接插入排序是稳定的排序算法,而直接选择排序是不稳定的排序算法,在使用时应注意这一点。
原文:https://www.cnblogs.com/fangtingfei/p/11520634.html