项目中最主要的点在于:找出两个站点之间通过最少站数的路线。该点对应的经典模型是“在一个无向图中找出两点之间的最短路径”。各个站点即为无向图中的点,两站间的路径即为无向图中连接两个节点的边,在此需求下,所有边的长度均为1。
地铁最短路的换乘,最贴近实际的情况是“一次初始化,多次查询”,即在地图确定下来之后可能会有若干次不同点对的查询。而本需求中地铁线路图数据需要与执行程序解耦,每次查询对于地图数据都可能是不同的,所以初始化的时间应该均摊到每次查询中去。由于地铁地图属于稀疏图,故可以用SPFA算法解决。
细节上,为了解决两条线路覆盖的情况下(见下图),连续换乘的问题,需要更好的换乘算法。
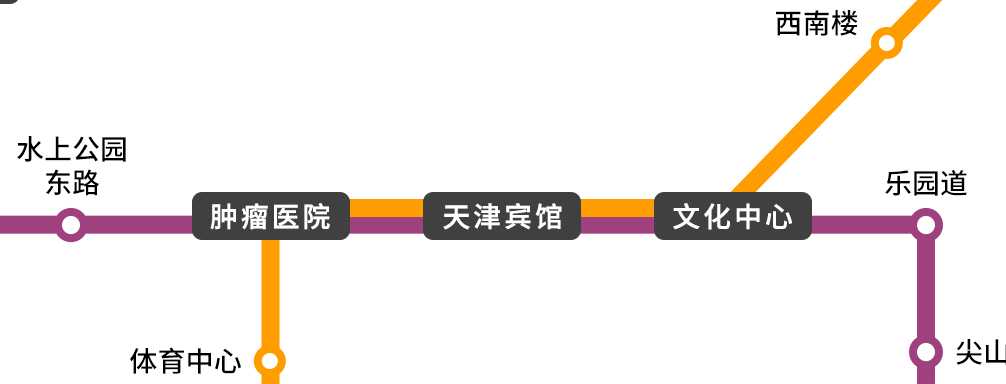
解决方法:通过判断站点和前继站点的所在线路是否有重叠来判断是否需要换乘。
数据存储上,可以采用存点/存边两种形式。在本项目中,存边会明显优于存点。
具体到内容,整个数据文件可以被几条线路分成几个大的模块,每个模块存一条线路的数据,由于地铁站名不存在同名的情况,可以不存线路换乘站点的信息,通过同名同名判断即可。由于同一条边不可能同时属于两条线路,所以在边信息上不会存在冗余。每个模块由一个星号(*)开始,后面这个这条线的名称。接下来包含若干条边信息。每条边信息的格式为起点站名称 终点站名称。每条线的起点可以由建图后入度为 0 的点确定。
样例如下:
* 1号线
刘院 西横堤
果酒场 本溪路
...(省略)
咸水沽北 双桥河
* 9号线
天津站 大王庄
大王庄 十一经路
...(省略)原文:https://www.cnblogs.com/Keadin/p/11545945.html