试图找到一条直线,使所有样本到直线上的欧式距离之和最小
cost function,往往令其最小化
单变量线性回归假设函数
\[
h(\theta)=\theta_0+\theta_1x\tag{3.1}
\]

不停进行\(\theta\)迭代计算使代价函数J最小化

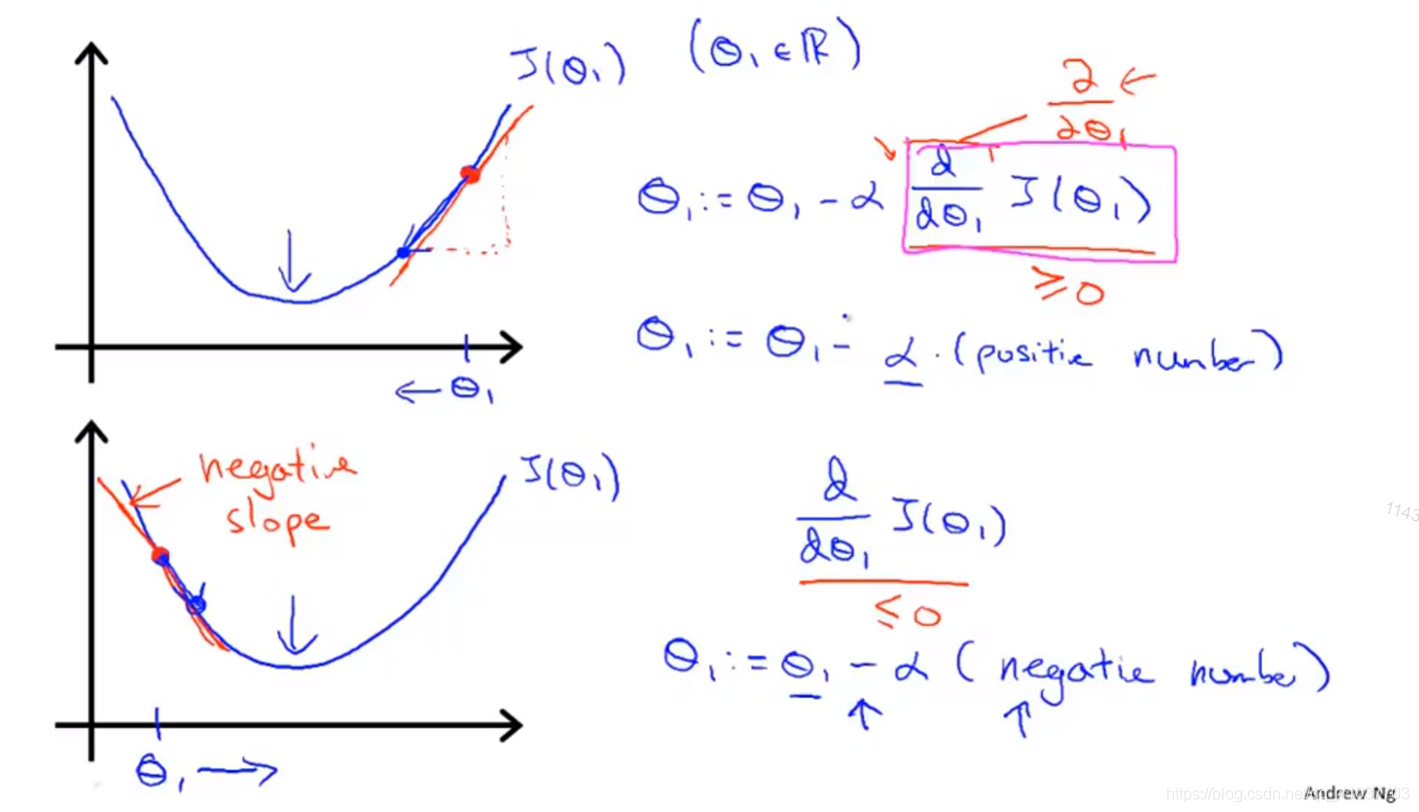
每次梯度下降均使用整个训练集的数据
\[ J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)^2\tag{3.2} \]
? 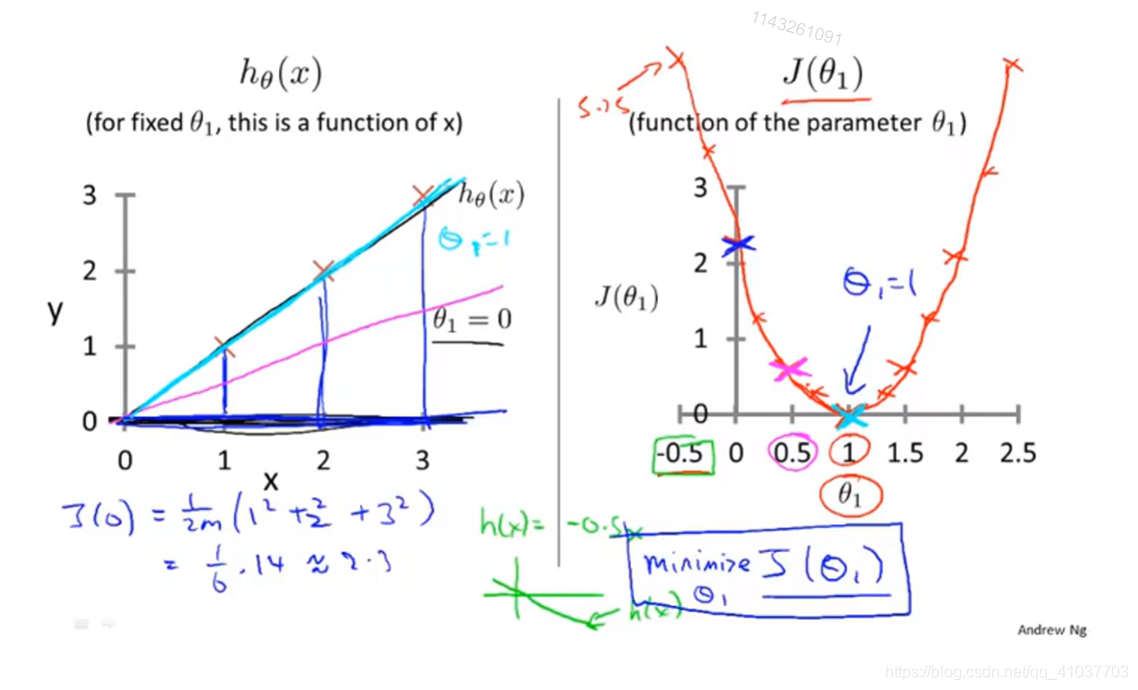
多元即多个未知数\(x\),多个参数\(\theta\),其中\(x_0=1\)
\[
h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n=\theta^Tx\tag{3.3}
\]
\[ x=\left[\begin{matrix}x_0\\x_1\\x_2\\\vdots\\x_n\end{matrix}\right] \theta=\left[\begin{matrix}\theta_0\\\theta_1\\\theta_2\\\vdots\\\theta_n\end{matrix}\right] \]

增快梯度下降速度的技巧
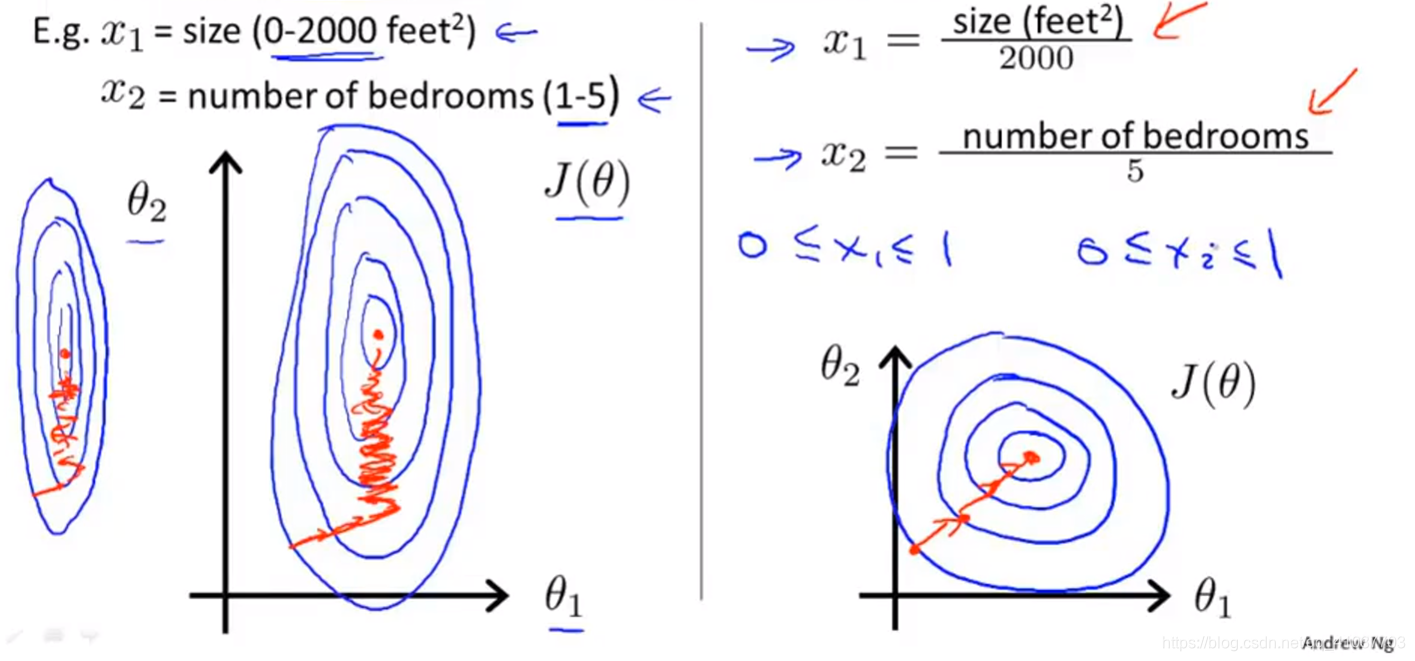
确保代价函数下降正确方法
可依据经验选择不同特征进行线性回归
无需进行多次迭代运算即可得到合适的参数\(\theta\)值使代价函数下降到最小
\[
\theta=(X^TX)^{-1}X^Ty\tag{3.4}
\]
X为特征矩阵,y为特征计算的真实值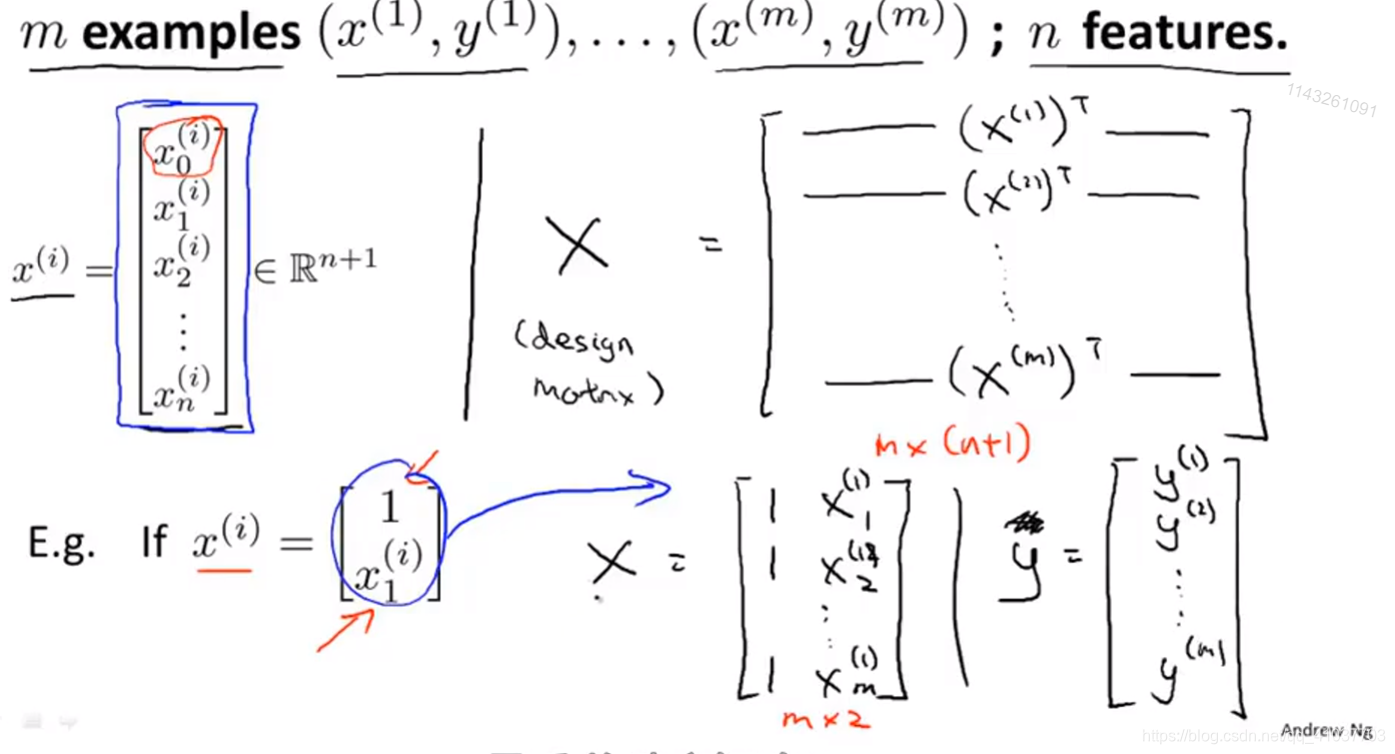
| 梯度下降法 | 正规方程 | |
|---|---|---|
| 缺点 | 1.需要选择学习率\(\alpha\) 2.需要多次迭代计算 |
1.\((X^TX)^{-1}\)计算复杂 |
| 优点 | 计算速度受特征变量维度影响小 | 1.无需考虑学习率 2.无需进行迭代计算 |
有关代码风格
\[ \theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2x_j^{(i)} \]
matlab中,inv(A)*B速度比A\B慢,\代表求解线性方程组Ax=B
\[
inv(X'X)X==(X'X)\setminus{X}
\]
进行对应列运算时,可采用bsxfun(fun,A,B)实现,速度更快
多元变量情况下,采用向量化计算更快
\[
J(\theta)=\frac{1}{2m}(X\theta-\stackrel{\rightarrow}{y})^T(X\theta-\stackrel{\rightarrow}{y})
\]
针对多元变量的线性回归,预测新数据时需要把新数据标准化后再将矩阵右侧加一列
实际上无需编些\(J(\theta)\)只需编写其偏导数,但为了监控\(J(\theta)\)的值确保梯度下降法正确工作,需要记录代价函数每次更新的量
opptions=optimset('Gradobj','On','MaxIter','100');
initialTheta=zeros(2,1);
[jVal,gradient]=costFunction(theta);%gradient表示梯度,即代价函数对各个参数的偏导
[optTheta,functionval,exitFlag]=fminunc(@costFunction,initialTheta,options);%@表示地址,fminunc可使代价函数最小化
%该函数要求参数至少为二维
%利用设定的高级函数计算代价函数最小化时的参数值%反向传播
thetaVec=[Theta1(:) ; Theta2(:) ; Theta3(:)];
DVec=[D1(:) ; D2(:) ; D3(:)];
Theta1=reshape(thetaVec(1:110),10,11);
Theta2=reshape(thetaVec(111:220),10,11);
Theta1=reshape(thetaVec(221:231),1,11);
maltab中sum(A.^2)与A*A‘的值有略微不同
编程时注意使用矩阵,使函数满足不同维数的情况
SVM程序包一般会自动加上偏置量\(x_0=1\),因此无需额外添加
使用svmTrain时记得应用训练集而不是交叉验证集
原文:https://www.cnblogs.com/jestland/p/11548483.html