聚类试图将数据集中的无标记样本划分为若干个通常不相交的子集,每个子集称为一个簇(cluster),每个簇可能对应于一些潜在的概念
原则:同一簇样本尽可能相似,不同簇样本尽可能不同,即簇内相似度高 簇间相似度低
闵可夫斯基距离
\[
dist_{mk}(x_i,x_j)=(\sum^{n}_{u=1}|x_{iu}-x_{ju}|^p)^{\frac{1}{p}}\tag{12.1}
\]
p=2:为欧氏距离
p=3:为曼哈顿距离
p趋于无限时,为切比雪夫距离
输入:想要的簇的个数K
? 无标记的样本({x1,x2...xm}
迭代:预先设置K个点作为K个簇中心
? 计算m个样本分别与K个中心点的距离,其中最近的距离设定同类\(c_i=\underset{k}{\text{min}}||x^{(i)}-\mu_k||^2\)
? m个样本分类完成后,对各类求均值作为新的簇中心,依据新的中心重新对m个样本分类
? 当计算的中心位置与上一次相同时停止迭代
\[ J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_k)=\underset{c,\mu}{\text{min}}\frac{1}{m}\sum^{m}_{i=1}||x^{(i)}-\mu_{c^{(i)}}||^2\tag{12.2} \]
可多次随机初始化,运行K-means算法多次。取目标函数最小的一次作为最优分类
由目的确定
肘部法则
常用的监督学习方法,给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于k个邻居进行预测,分类任务可用投票法,回归任务可用平均法
高维属性导致数据样本稀疏,距离计算困难,需要通过某种数学变换将原始高维属性空间转变为一个低维子空间
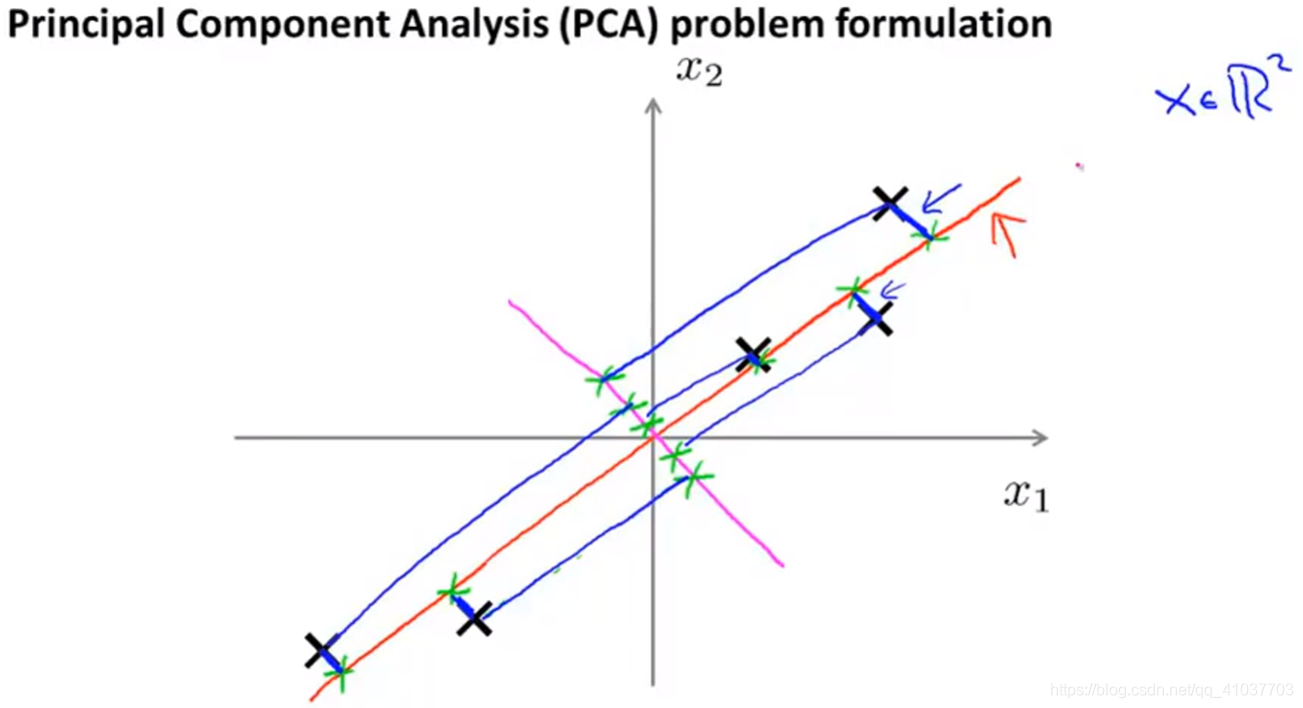
PCA可寻找一个超平面使样本的投影距离之和最小(蓝色线段)
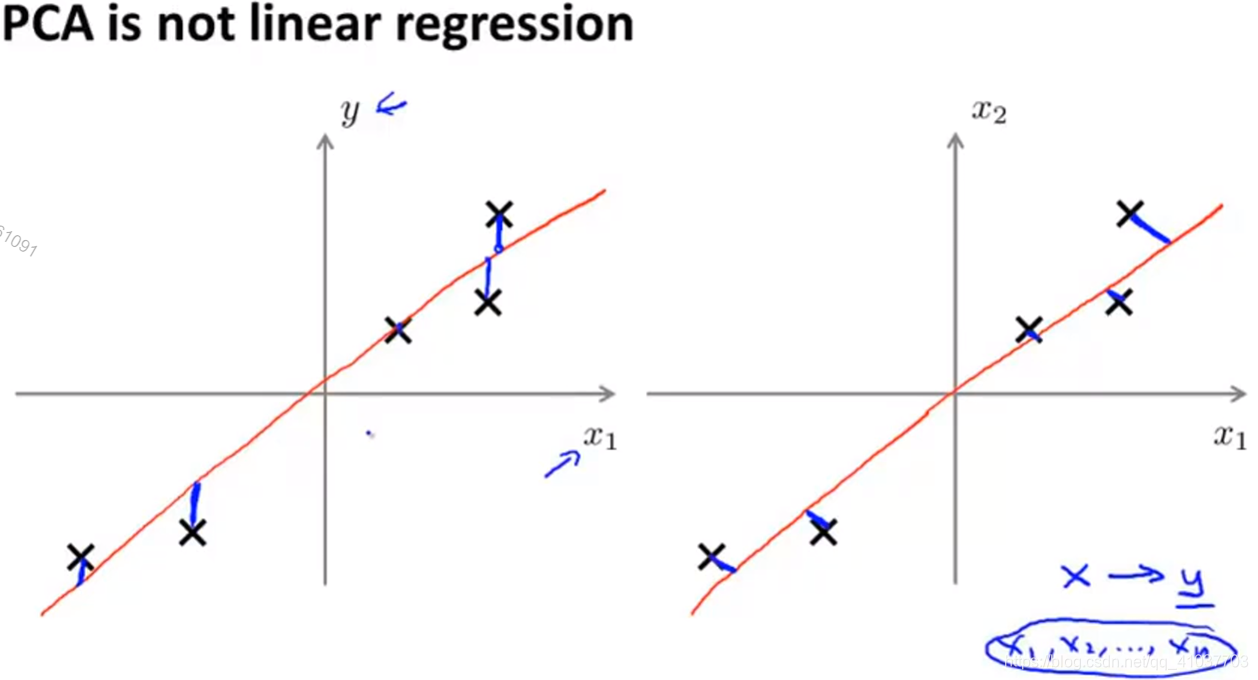
PCA:最小化正交距离
数据预处理:均值标准化 ,即让每个样本减去均值
? 特征缩放:若不同特征规模不同,在均值标准化后除以特征的标准偏差
计算降维的新坐标z
U即为特征向量矩阵,代表了样本特征的主成分;S为对角矩阵
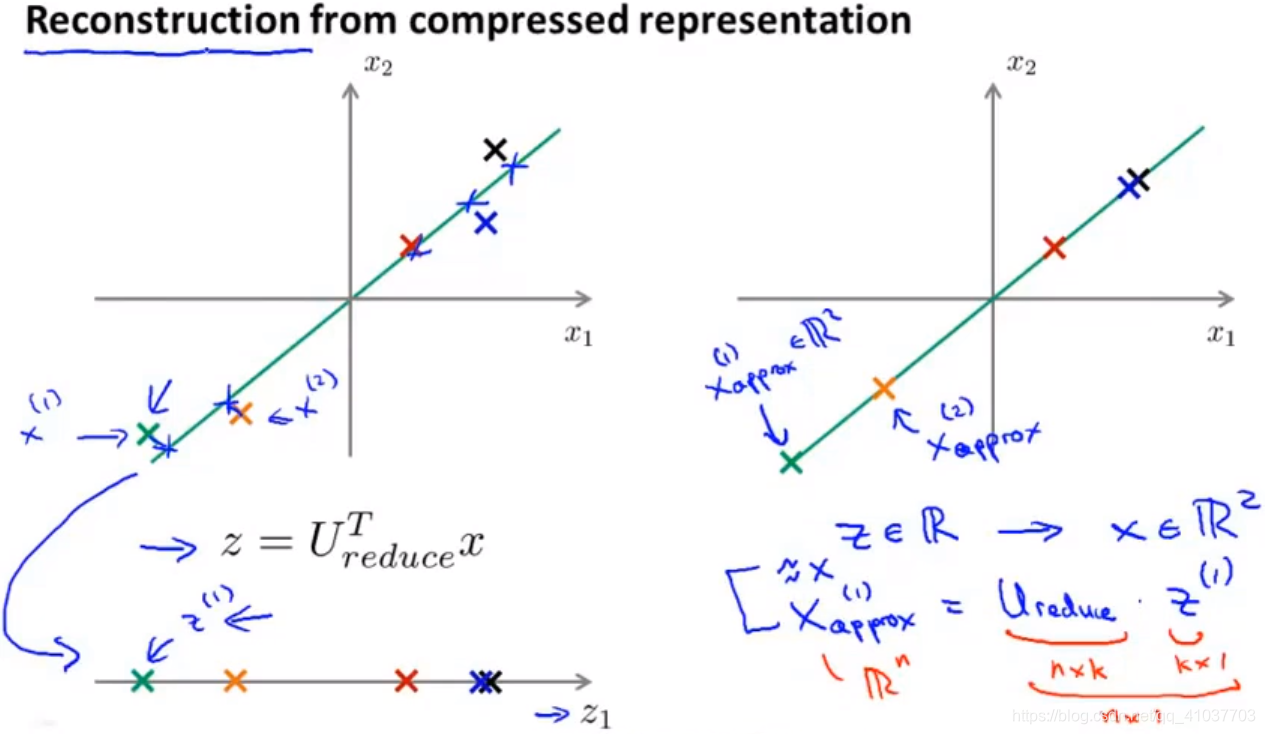
更新K值,确保降维后方差保留绝大部分原方差 其中,\(x_{approx}\)是在高维空间中映射到低维平面上的近似点,$x_{approx}=U_{reduce} \cdot z $
其中,\(x_{approx}\)是在高维空间中映射到低维平面上的近似点,$x_{approx}=U_{reduce} \cdot z $
需要找到满足不等式最小的k
原文:https://www.cnblogs.com/jestland/p/11548534.html