吴恩达机器学习入门笔记9-支持向量机

9 支持向量机-SVM

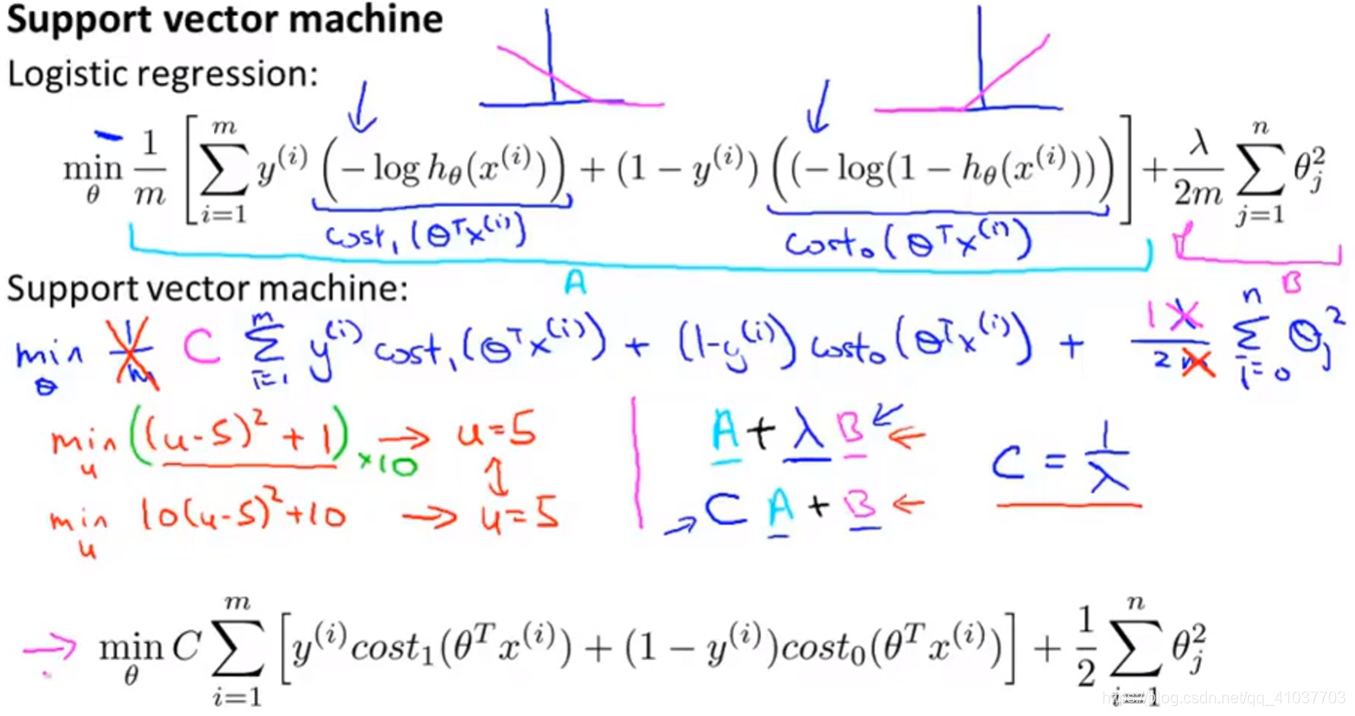
相比于神经网络，不用担心陷入局部最优问题，因为是凸优化

9.1 支持向量机的假设函数

\[ h_{\theta}(x)=\left\{\begin{array}{ll}{1,} & {\text { if } \theta^{T} x \geq 0} \\ {0,} & {\text { other }}\end{array}\right.\tag{9.1} \]
最小化上式，得到参数\(\theta\)后下次代入为SVM的假设函数，

9.2 支持向量机的决策边界

• 当C非常大时，SVM会尽可能将所有样本点正确分类，SVM的决策边界会因特殊点而发生较大变化。SVM会将样本以最大间距分开

• 决策边界与参数向量\(\theta\)垂直
• 即使\(\theta_0\)不等于0，即参数向量或决策边界不过原点，最优化目标函数的效果也几乎相同
• SVM实际上是改变参数，使投影到参数向量上的样本向量距离原点的长度最大，即\(p^{(i)}.||\theta||\)中的\(p^{(i)}\)最大，同时所需的\(||\theta||\)最小。则可实现\(\text{min}\frac{1}{2}\sum_{j=1}^{n}\theta^2_j\)
• 由此SVM也称大间距分类器

9.3 核函数

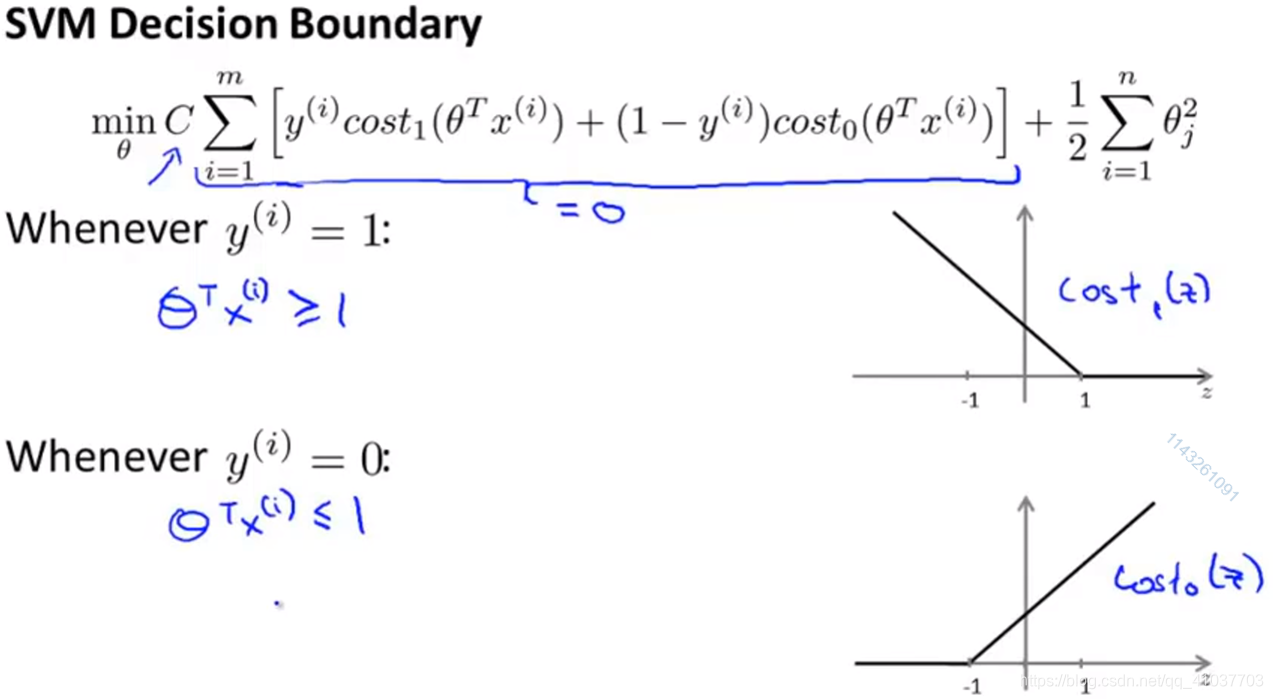
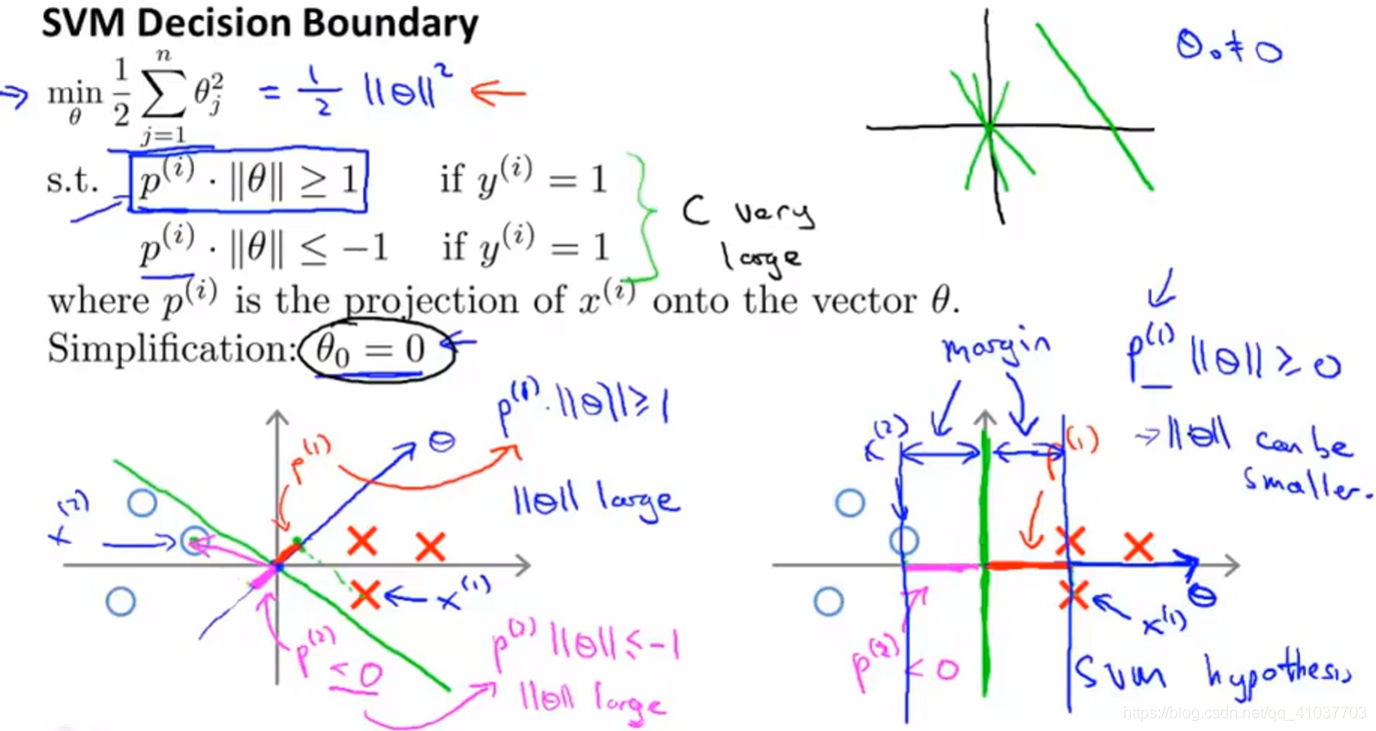
SVM采用该方法可解决非线性问题

9.3.1 高斯核函数-相似度方程之一

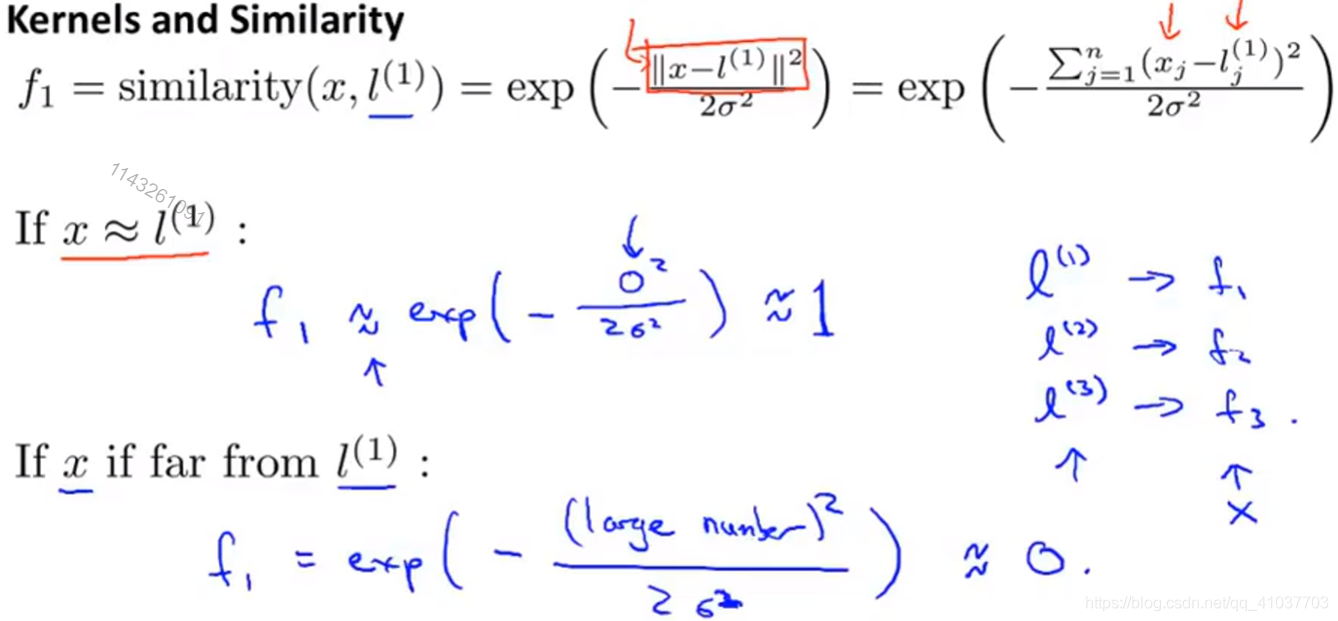
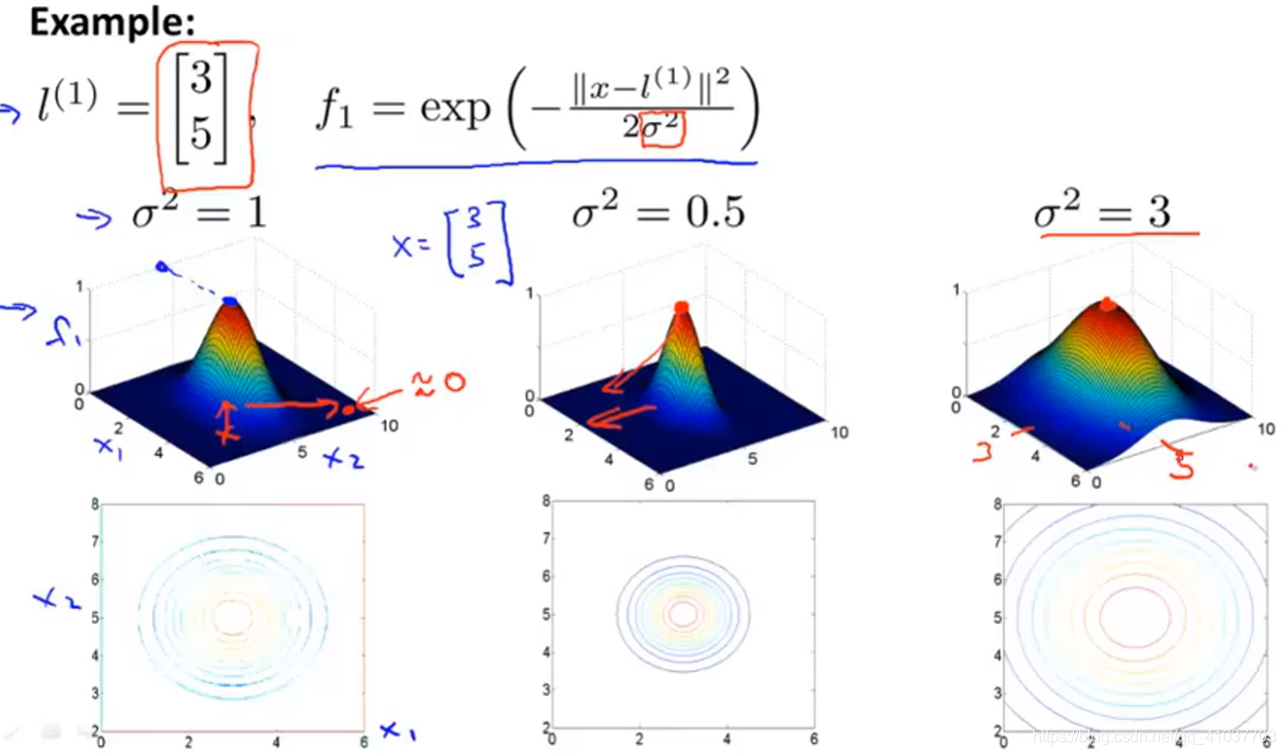
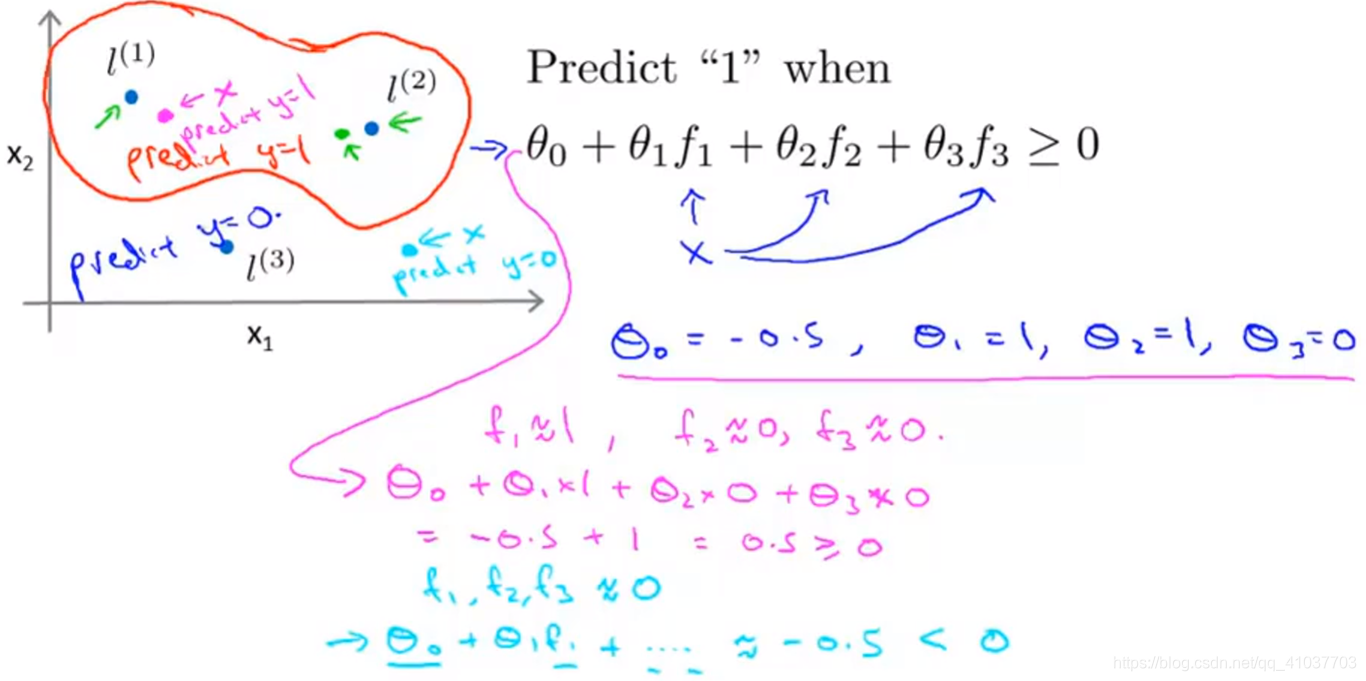
\(f\)即为样本X根据高斯核函数和标记计算得到的特征变量。

\(f\in[0,1]\)当训练好参数\(\theta\)后，根据一个样本x到不同标记的距离大小不同，特征变量不同，即赋予参数不同权重，最后计算出\(\theta^Tf\)，判断y=0或y=1，从而得到非线性边界

9.3.2 选取标记l的方法

将所有训练样本均作为标记点

9.3.3 线性核函数

即没有核参数的函数

9.3.4 多项式核函数

效果较差，针对非线性问题

9.4 支持向量机参数与偏差方差关系

9.4.1 C的选择

C(\(=\frac{1}{\lambda}\))大：即\(\lambda\)小，\(\theta\)大，意味着低偏差，高方差，倾向于过拟合

C(\(=\frac{1}{\lambda}\))小：即\(\lambda\)大，\(\theta\)小，意味着高偏差，低方差，倾向于欠拟合

9.4.2 \(\sigma^2\)的选择

\(\sigma^2\)大，特征量\(f\)随着x变化缓慢，即x变化很多，\(\theta^Tf\)变化很小，边界变化慢偏差较大

\(\sigma^2\)小，特征量\(f\)随着x变化剧烈，即x变化很小，\(\theta^Tf\)变化很多，边界变化快方差较大

9.5 使用SVM步骤

1. 选取参数C

2. 根据样本情况选取合适的核函数

3. 编写选取的核函数，输入样本生成所有的特征变量

4. 根据样本情况缩放样本比例

5. 若特征数量n(10000)>样本数m(10-1000)，使用逻辑回归或者线性核函数，因为数据少无法拟合复杂非线性函数

   若特征数量n(1-1000)<样本数m(10-50000)适中，使用高斯核函数，

   若特征数量n(1-1000)<样本数m(50000+)很大，带高斯核函数的SVM会运行很慢，手动创建更多特征变量，使用逻辑回归和线性核函数

吴恩达机器学习入门笔记9-支持向量机

原文：https://www.cnblogs.com/jestland/p/11548527.html