已知函数 \(f: \{1,2,3\}\to \{1,2,3\}\) 满足 \(f(f(x))=f(x)\), 则这样的函数有\(\underline{\qquad\qquad}\)个.
解析: 设 \(\{A,B,C\}=\{1,2,3\}\), 则 \(A\) 可表示集合 \(\{1,2,3\}\) 中任一元素, 又\[
f(A)=f(f(A))=f(f(f(A)))=\cdots.\] 如图, 图中 \[f=f_1=f_2=f_3=\cdots,\] 所以 \(f_k(k\geqslant 2,k\in\mathbb{N}^\ast)\) 中只能出现"平"射 \((\) 如 \(A\to A\) 型 \()\), 断然不可能出现"斜‘‘射 \((\) 如 \(A\to B\) 型 \()\),
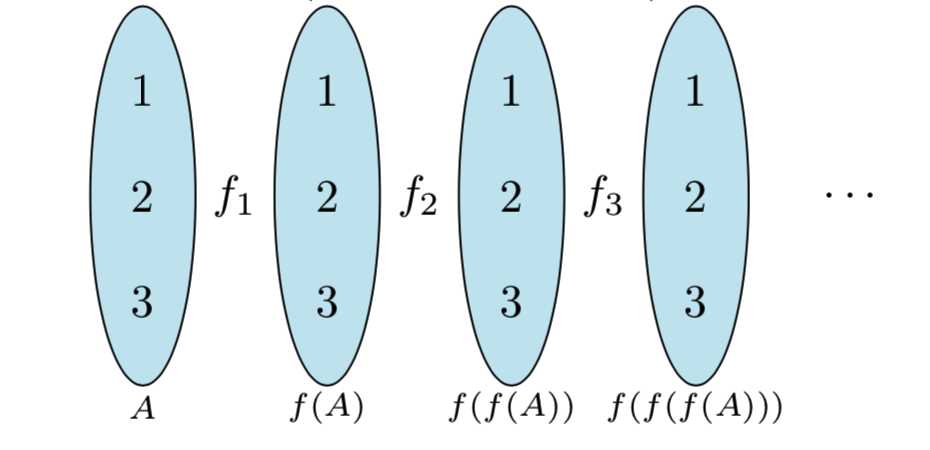
以下分类计数\(:\)
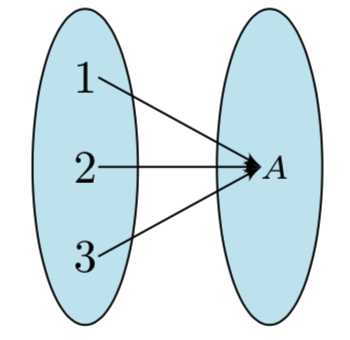
情形一 当 \(f(A)\) 的值域中只有一个元素时, 此时的满足题意的映射 \(f\) 有 \(\mathrm{C}_3^1\) 个, 如图
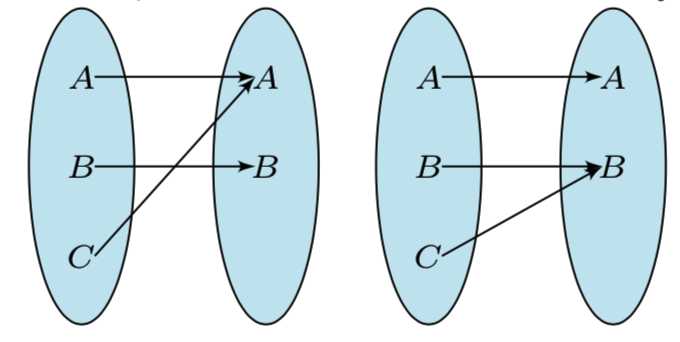
情形二 当 \(f(A)\) 的值域中只有两个元素时, 此时的满足题意的映射 \(f\) 有 \(\mathrm{C}_3^2\cdot \mathrm{C}_2^1\) 个, 如图
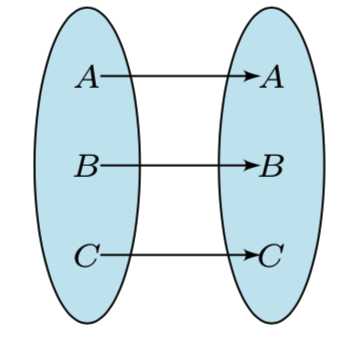
情形三 当 \(f(A)\) 的值域中有三个元素时, 此时的满足题意的映射 \(f\) 有 \(1\) 个, 如图
综上, 满足题意的函数 \(f\) 共计 \(10\) 个.
原文:https://www.cnblogs.com/Math521/p/11559859.html