题意简介:现有一个图,小Y要把它走完,每个点只去一次,路径字典序最小。
分析:这道题我认为很重要的一个点就是它的数据范围。它只有两种 m=n-1 或 m=n。我们先考虑第一种:m=n-1也就是边为节点数减一,这种说法已经很隐晦了,其实这种情况就是树啊。树的遍历且字典序最小什么的应该很多人都会做吧,就只用深搜一下,这60分还是很好拿的。(由于每个点只做一次sort所以是不会超时的!)

void dfs_60(int u,int fa){ ans[++top]=u; int ver[1000],k; k=0; memset(ver,0,sizeof(ver)); for(int i=head[u];i;i=next[i]){ if(to[i]!=fa)ver[++k]=to[i]; } sort(ver+1,ver+k+1); for(int i=1;i<=k;++i){ dfs_60(ver[i],u); } return ; }
然后我们要想个办法解决一个m=n的情况,并且在前面60的基础上加一些改动以达到ac的效果。那么m=n到底是个什么呢?他叫做:基环树。用我的理解来说,就是树里有一个环(也可以说是随便将一棵树上本不相连的两个点连接)。他大概长什么样子呢(m=n):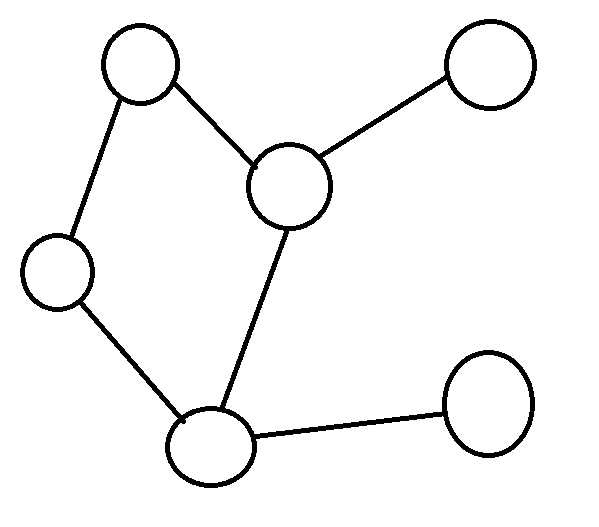
em,基本上是这个样子。其实啊,基环树这个东西,换句话说,只要删去环中的一条边也就变成了一棵树(多少颗不同的树取决于环的大小),那么我们可不可以删呢?在这道题当中是可以的。因为每一个点只去一次,就是说不存在从环上某个点走出去再沿着环返回这个点的这种情况,最多只走k-1条边(k为组成环的边数)。那么这道题我们从这k条边中每次取一条边出来删,按照m=n-1计算出最佳答案,最后所有的答案取最佳的就好。
那么目前只有一个问题:如何找环?
我是用的DFS,由于这道题只可能有一个环(因为m=n),所以就直接遍历,用一个栈存可能是环的点,遍历到已遍历的点的时候,就全部出栈直到那个点也弹出去。如果这个点所有子树搜完都没有找到环,那么把这个点出栈就行了。

void findh(int u,int fa){ if(flag==1)return; for(int i=head[u];i;i=next[i]){ if(to[i]!=fa){ if(vis[to[i]]){ while(to[i]!=st[top_st]){ h[++hsum]=st[top_st--]; } h[++hsum]=to[i]; flag=1; } else{ vis[to[i]]=1; st[++top_st]=to[i]; findh(to[i],u); if(flag==1)return; top_st--; vis[to[i]]=0; } } } }
接下来就任意删边用m=n-1弄就行了。注意一边搜索一边剪枝,不然会超时。
完整代码:

#include<iostream> #include<cstdio> #include<fstream> #include<cmath> #include<algorithm> #include<cstring> using namespace std; int read(){ char ch; int res=0,f=1; ch=getchar(); while(ch<‘0‘||ch>‘9‘){ if(ch==‘-‘)f=-1; ch=getchar(); } while(ch>=‘0‘&&ch<=‘9‘){ res=res*10+(ch-‘0‘); ch=getchar(); } return res*f; } const int MAXN=20005; int n,m,tot; int head[MAXN],next[MAXN],to[MAXN]; int ans[MAXN],top; int sz,sy,st[MAXN],top_st,vis[MAXN]; int h[MAXN],hsum,flag; int lans[MAXN],ltop,flag_dfs; void add(int x,int y){ to[++tot]=y; next[tot]=head[x]; head[x]=tot; } bool check(int u,int v){ if(u==sz&&v==sy)return 0; if(u==sy&&v==sz)return 0; return 1; } void dfs_60(int u,int fa){ ans[++top]=u; if(flag_dfs==0&&ans[top]<lans[top])flag_dfs=-1; if(flag_dfs==0&&ans[top]>lans[top])flag_dfs=1; if(flag_dfs==1)return; if(flag_dfs==-1&&top==n){ for(int i=1;i<=top;++i){ lans[i]=ans[i]; } flag_dfs=1; return; } int ver[1000],k=0; //memset(ver,0,sizeof(ver)); for(int i=head[u];i;i=next[i])if(to[i]!=fa&&check(u,to[i]))ver[++k]=to[i]; sort(ver+1,ver+k+1); for(int i=1;i<=k;++i)dfs_60(ver[i],u); return ; } void findh(int u,int fa){ if(flag==1)return; for(int i=head[u];i;i=next[i]){ if(to[i]!=fa){ if(vis[to[i]]){ while(to[i]!=st[top_st]){ h[++hsum]=st[top_st--]; } h[++hsum]=to[i]; flag=1; } else{ vis[to[i]]=1; st[++top_st]=to[i]; findh(to[i],u); if(flag==1)return; top_st--; vis[to[i]]=0; } } } } int main(){ n=read();m=read(); for(int i=1;i<=m;++i){ int u,v; u=read();v=read(); add(u,v);add(v,u); } memset(lans,127/3,sizeof(lans)); if(n==m+1){ dfs_60(1,0); for(int i=1;i<=top;++i){ printf("%d ",ans[i]); } } else{ st[++top_st]=1; findh(1,0); sz=h[1],sy=h[hsum],top=0; dfs_60(1,0); for(int i=2;i<=hsum;++i){ sz=h[i-1],sy=h[i],top=0,flag_dfs=0; //memset(ans,0,sizeof(ans)); dfs_60(1,0); } } for(int i=1;i<=n;++i){ printf("%d ",lans[i]); } } return 0; }
注:我注释掉了一些初始化的操作,是因为反正存答案的时候会覆盖,只用把top清零就行了
原文:https://www.cnblogs.com/clockwhite/p/11559895.html