普里姆算法—Prim算法
算法思路:
首先就是从图中的一个起点a开始,把a加入U集合,然后,寻找从与a有关联的边中,权重最小的那条边并且该边的终点b在顶点集合:(V-U)中,我们也把b加入到集合U中,并且输出边(a,b)的信息,这样我们的集合U就有:{a,b},然后,我们寻找与a关联和b关联的边中,权重最小的那条边并且该边的终点在集合:(V-U)中,我们把c加入到集合U中,并且输出对应的那条边的信息,这样我们的集合U就有:{a,b,c}这三个元素了,一次类推,直到所有顶点都加入到了集合U。(普里姆算法是允许负数的,狄杰斯特拉算法不支持)
下面我们对下面这幅图求其最小生成树:
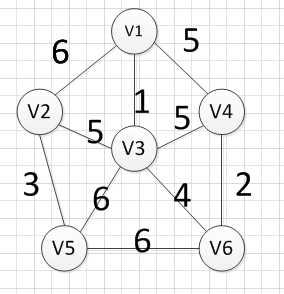
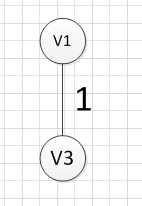
1.假设我们从顶点v1开始,所以我们可以发现(v1,v3)边的权重最小,所以第一个输出的边就是:v1—v3=1:
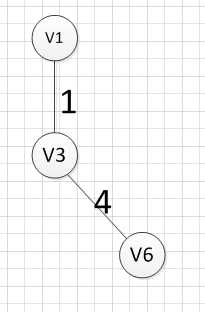
2.然后,我们要从v1和v3作为起点的边中寻找权重最小的边,首先了(v1,v3)已经访问过了,所以我们从其他边中寻找,发现(v3,v6)这条边最小,所以输出边就是:v3—-v6=4
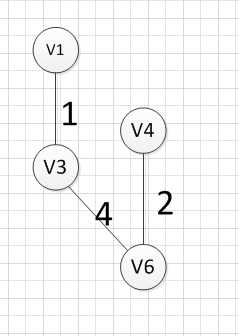
3.然后,我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边,我们可以发现边(v6,v4)权重最小,所以输出边就是:v6—-v4=2.
4.然后,我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边,发现边(v3,v2)的权重最小,所以输出边:v3—–v2=5
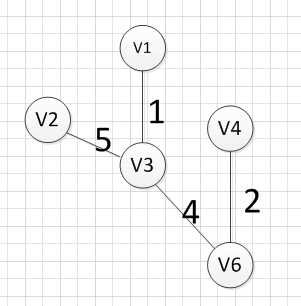
5.然后,我们就从v1、v3、v6、v4,v2这2五个顶点相关联的边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以输出边:v2—–v5=3
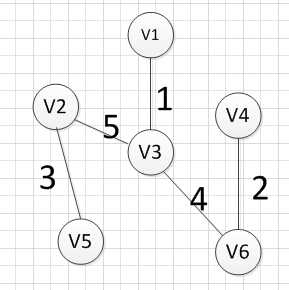
6.最后,我们发现六个点都已经加入到集合U了,我们的最小生成树建立完成。
原文链接:https://blog.csdn.net/qq_35644234/article/details/59106779
Prim算法
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
#define INF (~(0x1<<31))
typedef struct Graph
{
char vexs[MAX];
int vexnum;
int edgnum;
int matrix[MAX][MAX];
} Graph,*PGraph;
typedef struct EdgeData
{
char start;
char end;
int weight;
} EData;
static int get_position(Graph g,char ch)
{
int i;
for(i=0; i<g.vexnum; i++)
if(g.vexs[i]==ch)
return i;
return -1;
}
Graph* create_graph()
{
char vexs[]= {‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘};
int matrix[][7]=
{
{0,12,INF,INF,INF,16,14},
{12,0,10,INF,INF,7,INF},
{INF,10,0,3,5,6,INF},
{INF,INF,3,0,4,INF,INF},
{INF,INF,5,4,0,INF,8},
{16,7,6,INF,2,0,9},
{14,INF,INF,INF,8,9,0}
};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int i,j;
Graph *pG;
if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
return NULL;
memset(pG,0,sizeof(pG));
pG->vexnum=vlen;
for(i=0; i<pG->vexnum; i++)
pG->vexs[i]=vexs[i];
for(i=0; i<pG->vexnum; i++)
for(j=0; j<pG->vexnum; j++)
pG->matrix[i][j]=matrix[i][j];
for(i=0; i<pG->vexnum; i++)
{
for(j=0; j<pG->vexnum; j++)
{
if(i!=j&&pG->matrix[i][j]!=INF)
pG->edgnum++;
}
}
pG->edgnum/=2;
return pG;
}
void print_graph(Graph G)
{
int i,j;
printf("Matrix Graph: \n");
for(i=0; i<G.vexnum; i++)
{
for(j=0; j<G.vexnum; j++)
printf("%10d ",G.matrix[i][j]);
printf("\n");
}
}
EData* get_edges(Graph G)
{
EData *edges;
edges=(EData*)malloc(G.edgnum*sizeof(EData));
int i,j;
int index=0;
for(i=0; i<G.vexnum; i++)
{
for(j=i+1; j<G.vexnum; j++)
{
if(G.matrix[i][j]!=INF)
{
edges[index].start=G.vexs[i];
edges[index].end=G.vexs[j];
edges[index].weight=G.matrix[i][j];
index++;
}
}
}
return edges;
}
void prim(Graph G,int start)
{
int min,i,j,k,m,n,sum;
int index=0;
char prim[MAX];
int weight[MAX];
prim[index++]=G.vexs[start];
for(i=0; i<G.vexnum; i++)
weight[i]=G.matrix[start][i];
weight[start]=0;
for(i=0; i<G.vexnum; i++)
{
//i用来控制循环的次数,每次加入一个结点,但是因为start已经加入,所以当i为start是跳过
if(start==i)
continue;
j=0;
k=0;
min=INF;
for(k=0; k<G.vexnum; k++)
{
if(weight[k]&&weight[k]<min)
{
min=weight[k];
j=k;
}
}
sum+=min;
prim[index++]=G.vexs[j];
weight[j]=0;
for(k=0; k<G.vexnum; k++)
{
if(weight[k]&&G.matrix[j][k]<weight[k])
weight[k]=G.matrix[j][k];
}
}
// 计算最小生成树的权值
sum = 0;
for (i = 1; i < index; i++)
{
min = INF;
// 获取prims[i]在G中的位置
n = get_position(G, prim[i]);
// 在vexs[0...i]中,找出到j的权值最小的顶点。
for (j = 0; j < i; j++)
{
m = get_position(G, prim[j]);
if (G.matrix[m][n]<min)
min = G.matrix[m][n];
}
sum += min;
}
printf("PRIM(%c)=%d: ", G.vexs[start], sum);
for (i = 0; i < index; i++)
printf("%c ", prim[i]);
printf("\n");
}
int main()
{
Graph *pG;
pG=create_graph();
print_graph(*pG);
prim(*pG,0);
}
原文链接:https://blog.csdn.net/hhu1506010220/article/details/51971717
原文:https://www.cnblogs.com/yuanch2019/p/11578802.html