已知函数 \(f(x)=\begin{cases} x\mathrm{e}^x,x\leqslant 0,\\ -x^2+3x,x>0, \end{cases}\) \(g(x)=\begin{cases} f(x),x\leqslant a,\\-2x+4,x>a. \end{cases}\) 若函数 \(g(x)\) 恰有两个零点, 则 \(a\) 的取值范围是 \((\qquad)\)
$\mathrm{A}. [0,2)\qquad $ \(\mathrm{B}. [4,+\infty)\qquad\) $\mathrm{C}. [0,2)\cup[4,+\infty)\qquad $ \(\mathrm{D}.[0,2)\cup[3,+\infty)\)
解析: 如图, 容易画出 \(y=f(x)\) 与 \(y=-2x+4\) 的图象, 因此可得关于参数 \(a\) 的讨论分界点 \(0,2,3\).
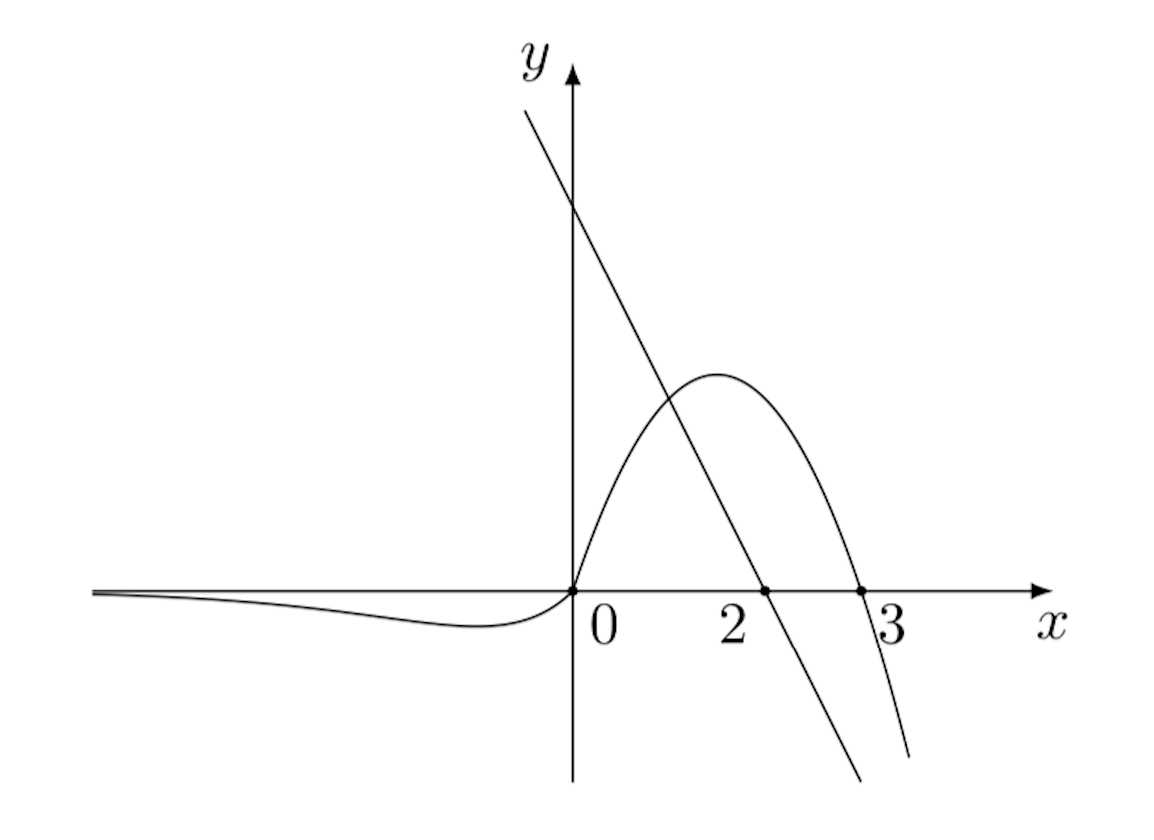
情形一 当 \(a\geqslant 3\) 时, \(y=f(x),x\leqslant a\) 有两个零点, \(y=-2x+4,x>a\) 没有零点. 满足题设.
情形二 当 \(2\leqslant a <3\) 时, \(y=f(x),x\leqslant a\) 有一个零点, \(y=-2x+4,x>a\) 没有零点. 不符题设.
情形三 当 $ 0\leqslant a<2$ 时, \(y=f(x),x\leqslant a\) 有一个零点, \(y=-2x+4,x>a\) 有一个零点. 满足题设.
情形四 当 $ a<0$ 时, \(y=f(x),x\leqslant a\) 没有零点, \(y=-2x+4,x>a\) 有一个零点. 不符题设.
综上可得 \(a\) 的取值范围为 \([0,2)\cup[3,+\infty)\). 因此选项 \(\mathrm{D}\) 正确.
原文:https://www.cnblogs.com/Math521/p/11583435.html