经过40多分钟才写出来,应该还是思路的问题。
但是通过了我就很开心
1 class Solution: 2 def judgeSquareSum(self, c: int) -> bool: 3 if c==0: 4 return True 5 6 i=int((c//2)**0.5) 7 j=int((c//2)**0.5)+1 8 while i<int(c**0.5)+1 and j>=0: 9 if i**2+j**2==c: 10 return True 11 elif i**2+j**2>c: 12 j=j-1 13 elif i**2+j**2<c: 14 i=i+1 15 else: 16 return False

if c <= 2: return True while c % 2 == 0: c = c // 2
做因数分解的同时,判断素因数的类型和幂次:
p = 3
while p * p <= c:
index = 0
while c % p == 0:
index += 1
c = c // p
if (p % 4 == 3) and (index % 2 == 1):
return False
p += 2
#分解到最后的c实际上是一个素数,这时候如果判断c是形如4k+1的素数,那肯定可以写为两整数平方和(也可以判断不是形如4k+3的素数也行) 这个不太看得透。。。
return c % 4 == 1
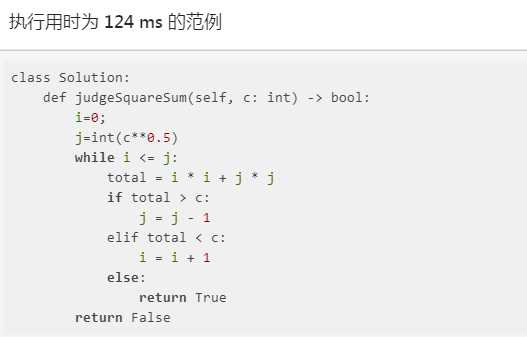
这个跟我的思路一样,但是比我写的简洁清爽。
while i <= j: total = i * i + j * j
这一句用得很棒。
这就是区别啊,明明也想到了,但是就差一个火候
原文:https://www.cnblogs.com/taoyuxin/p/11584096.html