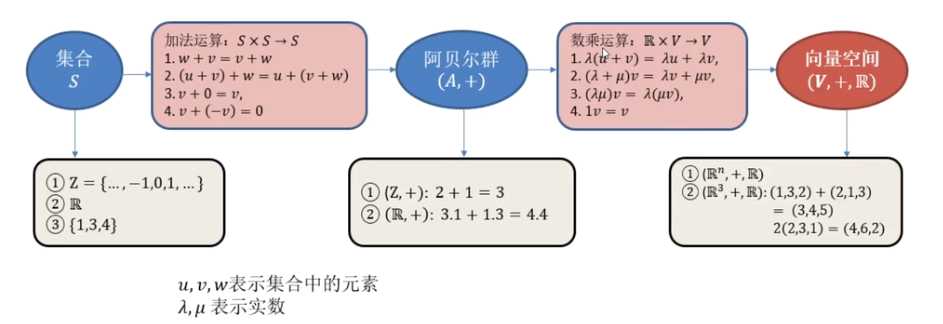
集和 - 具备某种特定性质的事物的总体,可有限,可无限, 可以理解为某种相似数据的集成 ( 如, 整数集, 实数集 )
空间 - 满足一定条件的集和
向量 - 具备大小和方向的量
向量空间 - 满足了加乘运算的集和
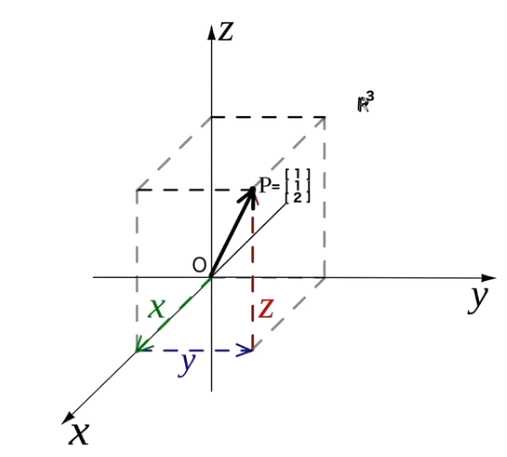
较为常见的是 n 维空间 ![]() , n 表示空间的维度, 当 n = 3 的时候, 可以理解为一个被取定了坐标系的三维空间
, n 表示空间的维度, 当 n = 3 的时候, 可以理解为一个被取定了坐标系的三维空间
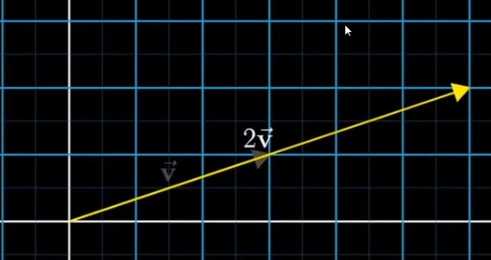
空间内的每一个组都可以被一组实数列表来进行表示, 列表中的每个点为该坐标轴上的投影
向量 - 向量空间的元素为向量

代数角度 - 同位置相加,
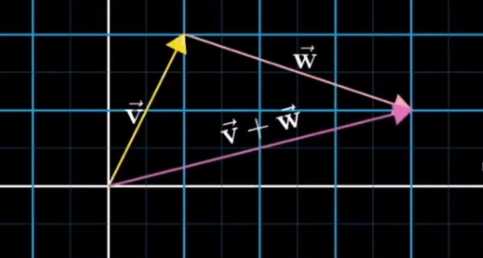
几何角度 - 按照某一个向量平移后首位相连, 计算新向量
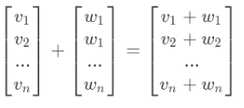
代数角度 - 变量于实数相乘, 变量中的所有数字于实数相乘即可
几何角度 - 变量在空间中的伸缩
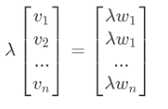
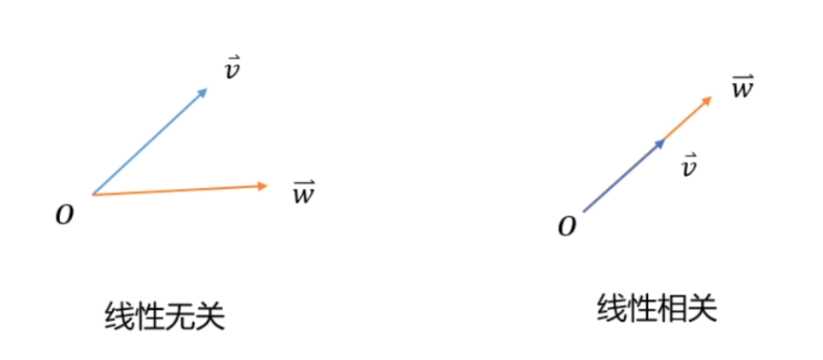
向量组 - 若干个 同维度 的列向量( 或 行向量 ) 所组成的 集和
线性组合 - ↓

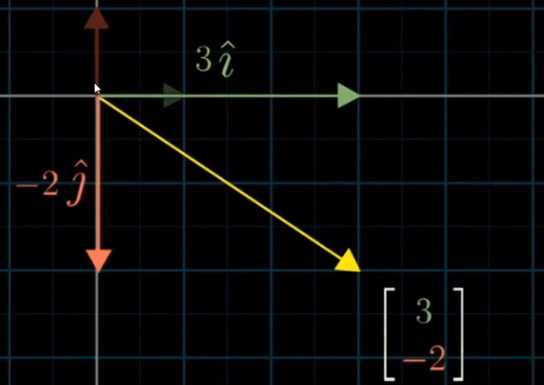
向量空间中的任何一个变量. 都可以看做是对基向量的缩放和相加操作
都可以写成两个向量的线性组合, 如图的 ![]()
![]()
不断的调整 ![]() 和
和 ![]() 可以得到无数的新向量, 而这些新向量的组成的集和, 就叫做张成空间
可以得到无数的新向量, 而这些新向量的组成的集和, 就叫做张成空间
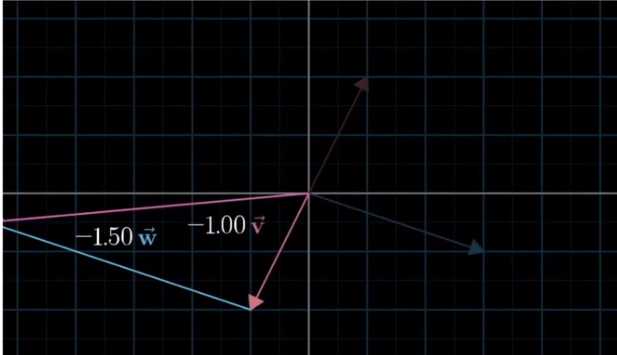

从代数的角度来说 , 内积是两个向量之间的一种运算, 结果为一个实数

范数定义了向量空间里面的距离, 最终结果依旧是个实数, 它的出现使得向量之间的比较成为了可能
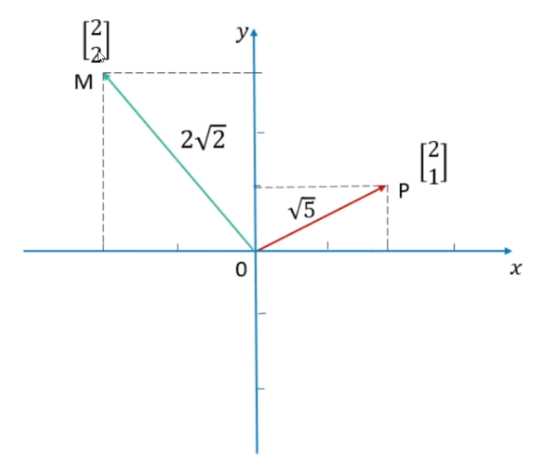
一维空间中, 4, 5 两个实数的比较很容易, 但是多维度空间中的 [2,2] 和 [2,1] 如何比较?
转化为范数后即可, 范数本质上是个 函数,
常用的范数有
L1 曼哈顿距离 , 函数运算为 绝对值计算
L2 欧几里得范式, 函数的运算为 平方再开方

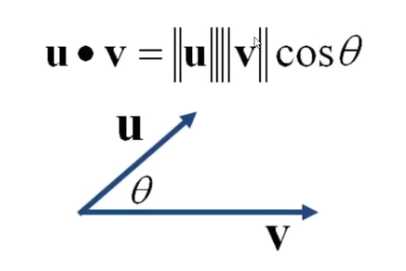
在了解了范数的原理之后, 就可以在几何角度上解释内积
内积定义了向量空间里的角度
u 和 v 的内积结果就是他们的 长度 * 角度
原文:https://www.cnblogs.com/shijieli/p/11589688.html