有一栋100层高的大楼,给你两个完全相同的玻璃球。假设从某一层开始,丢下玻璃球会摔碎。那么怎么利用手中的两个球,用什么最优策略知道这个临界的层是第几层?
第一次扔k层 ,则次数time=1,第二次,如果破了,要试从1到k-1层,此时需要Time=time+k-1=k 次;如果没破,还要扔k层,则次数为time=2;如果破了,还要扔k+1到2k-1层,再加上2 即Time=Time+k-2=k。还是K次;注意每多扔一次 少测试一层。次数却多一次。实际只要能测到n-1层就够了。
以此类推如果满足 k+(k-1)+(k-2)+(k-3)+(k-4)+....+2+1 >= n-1 。可以化简得到:k(k-1)>=2(n-1)
这里,n=100 所以 解得k=14。所以只要14次就可以确认那层试临界层。
首先从题目得出基本思路
1.第一个球应该低到高试,但不是每层必;
2.不能有侥幸心理,第二个球在第一个球的区间里每层必。
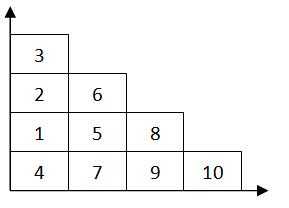
上图是简化为10层楼解法。数字代表楼层,球从原点先右后上的路径对应的方格中的数字进行测试.也就是第一个球测试4\7\9\10层.如果第一个球4层坏了,第二个球测试1\2\3。如果第一个球7层坏了,第二个球测试5\6。依次类推,肯定可以测出最终的层数。这样做摔4次肯定能得出结果,是最优的方案。
如果把上图的每一个层看作一个1*1的正方形。上图就近似一个等腰梯形,面积为4*4/2+4*0.5=10,也就是层数。推广开来,对于边长为N的图形,它所能测试的层数就是N*N/2+N*0.5。对于M层楼,最优方案只是上图的类推。将1到M按照上图类同的方法排布,并按照先右后上的路径。这肯定是最优解。也就是N*N/2+N*0.5〉=M。这里只要取得N的最小正整数就是最多的尝试次数。比如100层的情况是: N*N/2+N*0.5>=100。解得N的最小正整数解是14。
从数学证明的角度来看:最优解是怎样的呢?问题已经可以转化为在坐标系的原点出发,只能先右后上的,在相同的面积下,哪一种图形的使得原点到该图形的任意一点的距离的最大值最小。结论是:在相同的面积中,直角等腰的三角形到达面上的任意一点的最大距离是最小的。直角等腰三角形的斜边上任意一点到达原点的距离都是一样的,也是直角等腰三角形中距离原点最大的。利用反证法,如果还有比直角等腰三角形更好的图形,必然要挖去斜边上所有的点,但是把这些点放在哪里呢?放在哪里都比现在的位置远。
设f(a, b)为a个球做b次测试可以测试到的楼层数,可以确定的楼层数即为f(a, b) + 1,因为第1层不需测试,需要测试的楼层号仅仅为[2, f(a, b) + 1]共f(a, b)层,也就是a个球b次测试可以测试到的楼层数。考虑第1次测试,测试的楼层记为x:
1)如果球破了,就需要测试x下面的楼层,还剩下a-1个球b-1次测试,测试的楼层数为f(a - 1, b - 1)。
2)如果球没有破,那么需要测试x上面的楼层,还剩下a个球b-1次测试,测试的楼层数为f(a, b - 1)。
a个球b次测试为1)2)测试的楼层数及第1次测试了的1层,所以:
f(a, b) = f(a - 1, b - 1) + f(a, b - 1) + 1 (1)
考虑初始条件,显然f(a, 1) = 1(a >= 1,1次测试可以测试到的楼层数当然为1,不论多少个球),f(1, b) = b(b >= 1,1个球做了b次测试当然测试到了b层楼)。
强调一下:注意f(a, b)为测试到的楼层数,f(a, b)加上不需测试的楼层才是可以确定的楼层(f(a, b) + 1)。
一般来说,a >= 2(1个球意义不大),可以计算出f(2, 64) = 2080,f(3, 64) = 43744,f(4, 64) = 679120。

1 /* 2 * a balls, n floors, want to find the minimum number of floor 3 * where a ball drops will be broken. output the minimum number 4 * of drops 5 * METHOD: dynamic programming 6 * assum the answer is b, that is the number of drops 7 * f(a, b): the maximum number of floors, when a balls and b drops 8 * f(a, b) = 1 + f(a, b - 1) + f(a - 1, b - 1) 9 * obviously, f(a, 1) = 1; f(1, b) = b 10 */ 11 #include <stdio.h> 12 #include <stdlib.h> 13 #include <assert.h> 14 #include <string.h> 15 #define DEBUG 16 #define MAX_B 64 17 #define MAX_A 16 18 #define f(a, b) ff[a - 1][b - 1] 19 static unsigned int a, n; 20 static unsigned long long ff[MAX_A][MAX_B]; 21 static void init() 22 { 23 int i; 24 memset(ff, 0, sizeof(ff)); 25 /*f(a, 1) = 1*/ 26 for (i = 1; i <= MAX_A; i++){ 27 f(i, 1) = 1; 28 } 29 /*f(1, b) = b + 1*/ 30 for (i = 1; i <= MAX_B; i++){ 31 f(1, i) = i; 32 } 33 } 34 static unsigned long long do_find_min_drops(int i, int j) 35 { 36 if (f(i, j)) 37 return f(i, j); 38 f(i, j) = do_find_min_drops(i - 1, j - 1) + 39 do_find_min_drops(i, j - 1) + 1; 40 return f(i, j); 41 } 42 static void do_print_drops(int i, int j, unsigned long long min, 43 unsigned long long max) 44 { 45 if (min > max) 46 return; 47 if (1 == i){ 48 assert(j == max - min + 1); 49 for (i = min; i <= max; i++){ 50 printf("%5d", i); 51 } 52 printf("/n"); 53 printf("*************/n"); 54 return; 55 } 56 if (1 == j){ 57 assert(min == max); 58 printf("%5lld/n", max); 59 printf("*************/n"); 60 return; 61 } 62 printf("%5lld", min + f(i - 1, j - 1)); 63 do_print_drops(i - 1, j - 1, min, min + f(i - 1, j - 1) - 1); 64 do_print_drops(i, j - 1, min + f(i - 1, j - 1) + 1, max); 65 } 66 static void print_drops(int ans) 67 { 68 do_print_drops(a, ans, 2, n);/*[2..n]*/ 69 } 70 static void find_min_drops() 71 { 72 /*NOTE: number of floors are [1, n]*/ 73 int i, j, m; 74 int ans; 75 #if 0//def DEBUG 76 for (i = 2; i <= MAX_A; i++){ 77 for (j = 2; j <= MAX_B; j++){ 78 printf("f(%d, %d) = %lld/n", i, j, do_find_min_drops(i, j)); 79 } 80 printf("****************/n"); 81 } 82 #endif 83 i = 1; 84 j = MAX_B; 85 while (i <= j){ 86 m = (i + j) / 2; 87 if (do_find_min_drops(a, m) + 1 < n) 88 /* 89 * why +1? because the 1st floor need not to test 90 */ 91 i = m + 1; 92 else 93 j = m - 1; 94 } 95 ans = i; 96 if (ans > MAX_B){ 97 printf("the number of the maximum drops(MAX_B = %d) is too small/n", MAX_B); 98 printf("maximum floors " 99 "can be tested is f(%d, %d) + 1 = %lld + 1. STOP/n", a, MAX_B, f(a, MAX_B)); 100 exit(0); 101 } 102 printf("the minimum drops: %d/n", ans); 103 print_drops(ans); 104 #ifdef DEBUG 105 for (i = 1; i <= a; i++){ 106 for (j = 1; j <= ans; j++){ 107 printf("f(%d, %d) = %lld/n", i, j, f(i, j)); 108 } 109 printf("****************/n"); 110 } 111 #endif 112 } 113 int main(int argc, char **argv) 114 { 115 if (3 != argc){ 116 fprintf(stderr, "usage: %s a n/n", argv[0]); 117 exit(-1); 118 } 119 120 a = atoi(argv[1]); 121 n = atoi(argv[2]); 122 printf("a = %d/tn = %d/n", a, n); 123 assert(a > 0 && a < MAX_A && n > 0); 124 init(); 125 find_min_drops(); /*drops: 1*/ 126 return 0; 127 }
1)2个球,100层楼时,可以计算出
f(2, 13) = 91 f(2, 14) = 105
因此需要的测试次数为14。
f(3, 8) = 92 f(3, 9) = 129
因此测试测试最多为9次。可以从38层开始。
[面试题][总结]100层楼丢玻璃球测试临界可破层数,用两个一模一样的球来测试计算尽可能少的次数?
原文:https://www.cnblogs.com/kuliuheng/p/11595153.html