1、线性变换的一个重要性质就是不包括平移,包含平移的变换称为防射变换。3D中的防射变换不能用3*3矩阵表达。
2、旋转:
在2D环境中,物体只能绕某个点旋转,2D中绕原点的旋转只有一个参数:角度,它描述了旋转量。逆时针为正

3、在3D环境中,绕轴旋转而不是点。
明确旋转轴指向那个方向。旋转轴在理论上市无线眼神的,但我们还是要认为有正端点和负端点。
左手法则:伸出左手,大拇指向上,其余四肢弯曲。大拇指指向旋转轴的正方向。四肢弯曲的方向就是旋转的正方向。
4、缩放矩阵

5、正交投影
一般来讲,投影意味着降维操作。
在某个方向上用零作为缩放因子。这种情况下,所有点都被拉平至垂直的轴3d或者2d上,平行投影或者正交投影。
6、向任意直线或平面投影
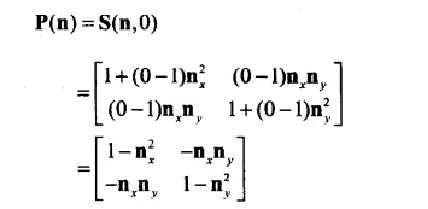

7、镜像:也叫做反射,是一种反射,其作用是将物体沿直线或平面翻转。
使缩放因子为-1能够狠容易的实现镜像变换。
注意:一个物体只能镜像一次,如果再次镜像(沿着不同的轴或平面的时候),物体将翻回正面。这和在
原位置旋转物体的效果是一样。
8、切变:
是一种坐标系扭曲变换,非均匀的拉伸他。切变的时候角度会发生变化,但面积和体积却都保持不变。
9、线性变换
F(a+b)=F(a)+F(b)
10、防射变换:
防射变换时指线性变换后接着平移。所以,防射变换的集合就是线性变换的集合。
v‘=vM+b的变换都是防射变换。
11、任何线性变换都能表达为矩阵,所以求逆变换等价求逆矩阵的逆,如果矩阵是奇异的,则变换不可逆,
可逆矩阵的行列式不为0。
12、如果变换前后2向量夹角的大小和方向都不改变,该变换时等角的。只有平移,旋转和均匀缩放时等角的。
任何等角变换都是防射和可逆的。
13、正交变换:
轴保持互相垂直,而且不进行缩放变换。
平移,旋转和镜像是仅有的正交变换。长度,角度,面积体积都保持不变。
14、刚体变换:
刚体变换只改变物体的位置和方向,不包括形状。 平移和旋转是仅有的刚体变换。
原文:http://www.cnblogs.com/xiao-wei-wei/p/3550465.html