在连通图 G 中,如果删除顶点 u 及从 u 出发的所有边后所得的子图不连通,我们就称顶点 u 为图 G 的关节点或连接点。
要解决这道题,我们可以检查图在单独删除各顶点之后的连通性,但这个算法要对每个顶点执行一次DFS, 效率不高。
不过,只要我们如下将DFS加以应用,就可以有效地找出图 G 中所有的关节点了。
在一次DFS中求以下变量值。
??prenum[u]:以 G 的任意顶点作为起点进行DFS,将各顶点 u 的访问(首次发现)顺序记录在prenum[u]中。
??parent[u]:通过DFS生成一棵树(DFS Tree),将其中结点 u 的父节点记录在parent[u]中。这里将DFS Tree记作T。
??lowest[u]:对于各顶点 u,计算下列情况的最小值并记入lowest[u]
① prenum[u]
② 存在 G 的Back(u, v)时,顶点 v 的prenum[v](Back(u, v)表示图 G 内 ”从顶点 u 出发指向 T 内的顶点 v“ 且 ”不属于 T “的边)
③ T 内顶点 u 的所以子节点 x 的lowest[u]
有了这些变量,我们便可以通过下述方法确定关节点。
① T 的根节点 r 拥有 2 个以上子节点时(充分必要条件),r 为关节点。
② 对于各顶点 u,设 u 的父节点parent[u] 为 p ,如果prenum[p] <= lowest[u] (充分必要条件),则 p 为关节点(p 为根节点时则套用 ①)。这表明顶点 u 及 u 在 T 中的子孙均不具备与 p 的祖先相连的边。
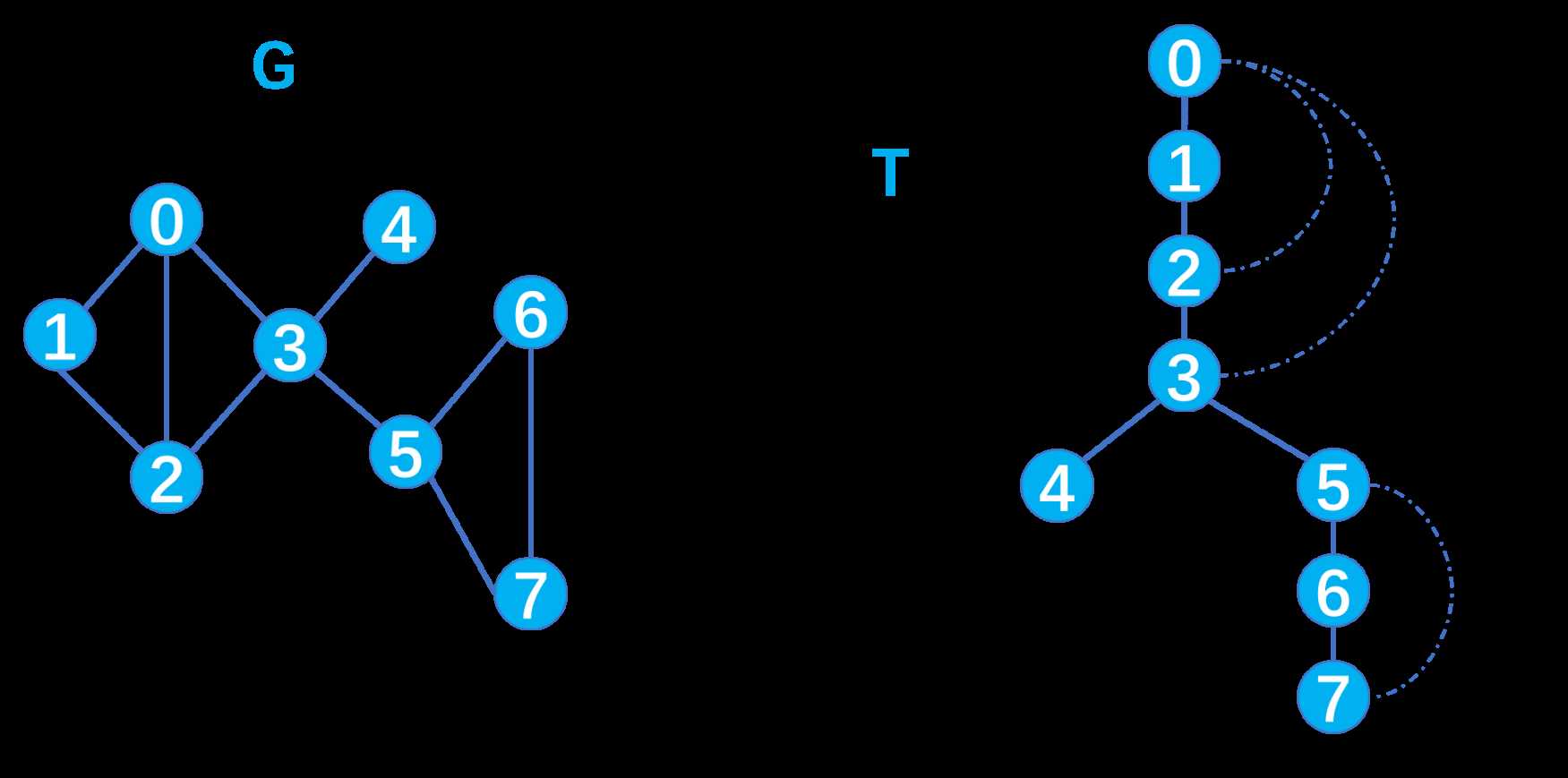
如图,G 代表图 G,T 代表以顶点 0 为起点对 G 执行DFS后得到的DFS Tree。T 的Back edges 用虚线标出,各顶点 u 的左侧数字为prenum[u]:lowest[u]。prenum[u]为DFS中各顶点 u 的被访问顺序:按照 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7的顺序记录。
lowest[u]是DFS过程中各顶点 u 访问结束的顺序:按照 4 -> 7 -> 6 -> 5 -> 3 -> 2 -> 1 -> 0的顺序算出。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=100000;
vector<int> G[maxn];
bool vis[maxn];
int N,prenum[maxn],parent[maxn],lowest[maxn],timer=1;
void dfs(int current,int prev);
void art_points();
int main()
{
int i,m,s,t;
cin>>N>>m;
for(i=0;i<m;i++)
{
cin>>s>>t;
G[s].push_back(t);
G[t].push_back(s);
}
art_points();
system("pause");
return 0;
}
void art_points()
{
int i,np=0,p;
set<int> ap;
dfs(0,-1);
for(i=1;i<N;i++)
{
p=parent[i];
if(p==0) np++;
else if(prenum[p]<=lowest[i]) ap.insert(p);
}
if(np>1) ap.insert(0);
for(set<int>::iterator it=ap.begin();it!=ap.end();it++)
cout<<*it<<endl;
}
void dfs(int current,int prev)
{
int next,i;
prenum[current]=lowest[current]=timer;
timer++;
vis[current]=1;
for(i=0;i<G[current].size();i++)
{
next=G[current][i];
if(!vis[next])
{
parent[next]=current;
dfs(next,current);
lowest[current]=min(lowest[current],lowest[next]);
}
else if(next!=prev)
lowest[current]=min(lowest[current],prenum[next]);
}
}
原文:https://www.cnblogs.com/VividBinGo/p/11600998.html