96. Unique Binary Search Trees

Given n, how many structurally unique BST‘s (binary search trees) that store values 1 ... n?

Example:

Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST‘s:

   1         3     3      2      1
    \       /     /      / \           3     2     1      1   3      2
    /     /       \                    2     1         2                 3

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            for(int j = 1; j <= i; j++){
                dp[i] += dp[j-1] * dp[i - j];
            }
        }
        return dp[n];
    }
}

自底向上的DP。递推公式下图可以理解，因为F(i, n)表示n个数字且以第i个为根的bst个数，所以两个循环都是小于等于。

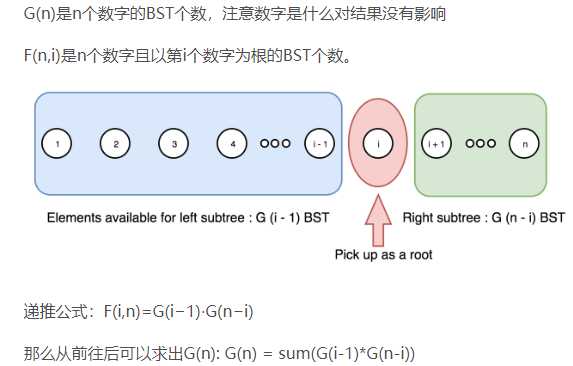
求和可从下图理解，本质上是因为，每个数都有资格作为root，所以答案当然要把他们加起来。

96. Unique Binary Search Trees

原文：https://www.cnblogs.com/wentiliangkaihua/p/11601268.html