在\(\triangle ABC\)中,角\(A,B,C\)所对的边分别是\(a,b,c\),若\(a\)\(=\)\(1\),且\(BC\)边上的高等于\(\tan A\),则\(\triangle ABC\) 的周长的取值范围为\(\underline{\qquad\qquad}\).
解析: 由题,不妨设\(c\geqslant b\).过\(A\)作\(BC\)直线的垂线,垂足为\(H\),
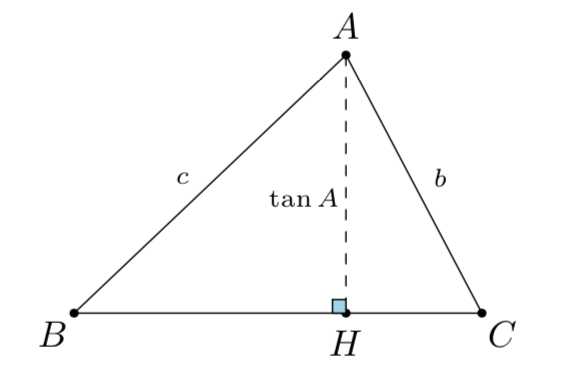
于是\[
\begin{split}
b+c=\dfrac{AH}{\sin C}+\dfrac{AH}{\sin B}=\dfrac{1}{\cos A}\cdot \left(\dfrac{a}{c}+\dfrac{a}{b}\right)=\dfrac{2(b+c)}{b^2+c^2-1}.
\end{split}\]
从而可得\(b^2+c^2=3,c\geqslant b\),另外考虑到\(a,b,c\)三边需满足构成三角形的充要条件,可得关于\(b,c\)的以下约束关系\[
\begin{cases}
& c\geqslant b>0,\ & b^2+c^2=3,\ & c-b<a=1,\ & b+c>1,\ \end{cases}\]
于是\(\triangle ABC\)的周长\(a+b+c\)的取值范围为\(\left(1+\sqrt{5},1+\sqrt{6}\right]\).
原文:https://www.cnblogs.com/Math521/p/11601185.html