Word2Vec是一个可以将语言中的字词转换为低维、稠密、连续的向量表达(Vector Respresentations)的模型,其主要依赖的假设是Distributional Hypothesis(1954年由Harris提出分布假说,即上下文相似的词,其语义也相似;我的理解就是词的语义可以根据其上下文计算得出)
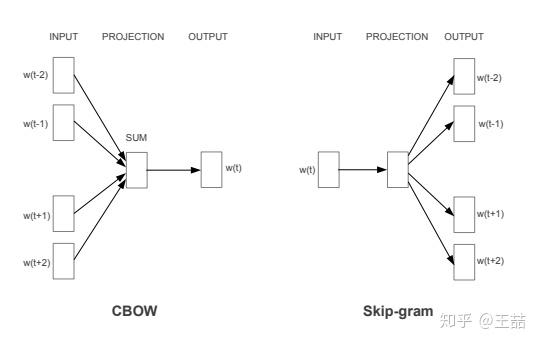
Word2vec主要分为CBOW(Continuous Bag of Words)和Skip Gram两种模式,其中CBOW是从原始数据推测目标字词;而Skip-Gram是从目标字词推测原始语句,其中CBOW对小型数据比较合适,而Skip-Gram在大型预料中表现得更好。
负采样的基本思想是用采样一些负例的方式近似代替遍历整个词汇。
\[ J^h( \theta ) = log \sigma( \Delta S_{\theta}(w,h)) + k log(1 - \sigma(\Delta S_{\theta}(w,h))) \]
\(其中h=w_1,...,w_n为上下文词序列\)
\(P_n(w)代表负样本分布为,w是抽样词\)
\(P_d(w)代表正样本(真实数据)分布\)
$ \sigma(x)=\frac{1}{1+e^{-x}}是sigmoid函数 $
$ \theta 代表模型参数$
\(k 代表负样本与正样本的比例\)
\(P^h( D=1|w,\theta ) = \frac{P^h_{\theta}(w)}{P^h_{\theta}(w)+kP_n(w)}=\sigma(\Delta S_{\theta}(w,h)) 代表在给定上下文h,参数\theta情况下w是正样本的概率\)
\(其中S_{\theta}(w,h)=\hat{q}(h)^T q_w + b_w = (\sum^n_{i=1}c_i \bigodot r_{w_i})^T q_w + b_w\)
\(\hat{q}(h) = \sum^n_{i=1}c_i \bigodot r_{w_i}是上下文词向量的线性加权,代表对目标词的估计值\)
\(c_i代表上下文词在位置i的权重向量\)
\(r_{w_i}代表上下文词i的词向量表示\)
\(q_w代表目标词的词向量表示\)
\(b_w代表上下文无关的偏置项\)
$ \frac{\partial }{\partial \theta} J^{h,w}(\theta) = (1-\sigma(\Delta S_{\theta}(w,h))) \frac{\partial }{\partial \theta}logP^h_\theta(w) - \sum^k_{i=1}[\sigma(\Delta S_{\theta}(w,h))\frac{\partial }{\partial \theta}logP^h_\theta(x_i)]$
公式中使用k个噪音样本的词向量加和来代替词典全部词汇的加和,所以NCE的训练时间只线性相关于负样本个数,与词典大小无关。
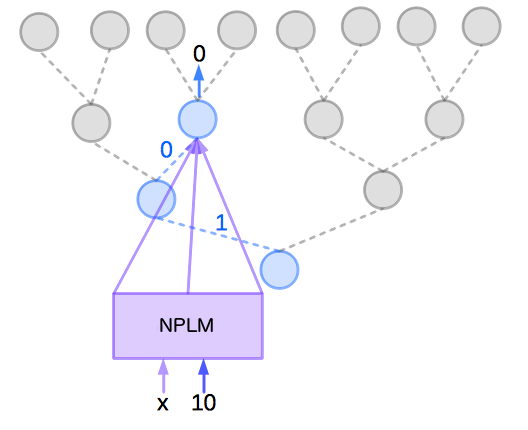
Hierarchical Softmax中不更新每个词的输出词向量,更新的是二叉树(哈夫曼树)上节点对应的向量。代价由??(|??|)变为??(\(??????_2|??|\))
$P( Y = y | X = x) = \prod_{j=1}^{m}P(b_{j}(y) | b_{j-1}(y),b_{j-2}(y),...,b_{1}(y), X=x)
$
其中\((b_{j?1}(y),b_{j?2}(y),...,b_1(y))\)为长度小于m的二进制表示,即是在二元分类树中的分支结点。
一种可以学习到结点间局部结构相似性的图表征算法;

加入了Alias sample(别名采样),可以对加权图做word2vec


原文:https://www.cnblogs.com/arachis/p/embedding.html