$\frac{1}{4}$遇到了一道水题,完全不会做,于是去请教小$D$。小$D$看了$0.607$眼就切掉了这题,嘲讽了$\frac{1}{4}$一番就离开了。于是,$\frac{1}{4}$只好来问你,这道题是这样的:
有$n$个球排成一行,每个球的颜色为黑或白。
执行$k$次操作,第$i(1\leqslant i\leqslant k)$次操作形式如下:
$\bullet$从$[1,n−i+1]$中,等概率随机选择一个整数$x$。
$\bullet$移除从左往右数的第$x$个球,或从右往左数的第$x$个球(也就是从左往右数的第$n−i+2−x$个)。之后,所有右侧的球的编号减$1$。
给定每个球的颜色信息,希望最大化移除的白球数量。
输出在最优策略下,期望的移除白球数量。误差在${10}^{−6}$范围内,即算正确。
从文件$v.in$中读入数据。
第一行,两个整数$n,k$。
第二行,一个长度为$n$、仅由$‘W‘$和$‘B‘$组成的字符串,第$i$个字符代表第$i$个球的颜色,$‘W‘$为白色,$‘B‘$为黑色。
输出到文件$v.out$中。
输出一行,一个浮点数,代表答案。
样例输入1:
3 1
BWW
样例输出1:
1.0000000000
样例输入2:
4 2
WBWB
样例输出2:
1.5000000000
样例$1$解释:
如果$x=1$,从右侧操作,如果$x=2$或$3$,从左侧操作,均可以移除一个白球。
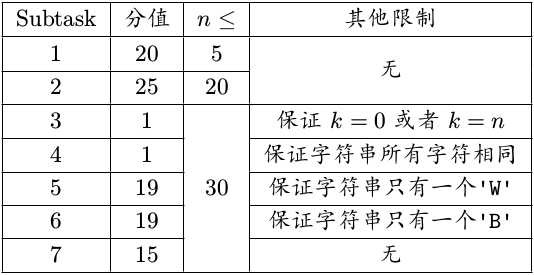
数据范围:
保证$1\leqslant n\leqslant 30,0\leqslant k\leqslant n$。
先来看$20$分的做法,我们可以使用状压$DP$解决,即为:
$$dp[i][sta]=\sum \max (dp[i-1][sta‘],dp[i-1][sta"])$$
剩下的我们可以记忆化搜索,用$map$存储已经出现过了的状态,加快转移速度。
但是这道题的数据卡了$map$,所以我们可以考虑$unordered_map+$大力卡常或者是手打$hash_map$,建议选择后者,既锻炼了手打$hash_map$的能力,又能感受到轻松$AC$此题的快感(不用卡常)。
状态数最多只有$\sum \limits_{i=0}^n\min\{2^i,C_n^i\}$,即为$\sum \limits_{i=1}^{n+1}Fib(i)$。
时间复杂度:$\Theta(\sum \limits_{i=1}^{n+1}Fib(i)\times n)$。
期望得分:$100$分。
实际得分:$100$分。
#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to,w;double v;};
struct hash_mp
{
int head[40000000],cnt;
rec e[6000000];
int len;
double &operator[](int sta)
{
int key=1LL*sta*len%30000019;
for(int i=head[key];i;i=e[i].nxt)
if(e[i].to==sta&&e[i].w==len)return e[i].v;
e[++cnt].nxt=head[key];
e[cnt].to=sta;
e[cnt].w=len;
e[cnt].v=-1.0;
head[key]=cnt;
return e[cnt].v;
}
}mp;
int n,k;
char ch[31];
int st;
double dfs(int x,int sta)
{
if(x==n-k)return 0.0;
mp.len=x;
if(mp[sta]>-0.5)return mp[sta];
mp[sta]=0;
st=sta;
bool Map[31];
for(int i=1;i<=x;i++)
{
Map[i]=st&1;
st>>=1;
}
for(int i=1;i<=x/2;i++)
{
double flag1=dfs(x-1,((sta>>(x-i+1))<<(x-i))|(sta&((1<<x-i)-1)))+Map[x-i+1];
double flag2=dfs(x-1,((sta>>i)<<(i-1))|(sta&((1<<i-1)-1)))+Map[i];
mp.len=x;
mp[sta]+=2.0/x*max(flag1,flag2);
}
if(x&1)
{
double flag=dfs(x-1,(sta>>(x-((x>>1)+1)+1))<<(x-((x>>1)+1))|(sta&((1<<(x-((x>>1)+1)))-1)))+Map[x/2+1];
mp.len=x;
mp[sta]+=1.0/x*flag;
}
return mp[sta];
}
int main()
{
scanf("%d%d%s",&n,&k,ch+1);
k=min(n,k);
for(int i=1;i<=n;i++)
{
st<<=1;
if(ch[i]==‘W‘)
st++;
}
printf("%.10lf",dfs(n,st));
return 0;
}
rp++
原文:https://www.cnblogs.com/wzc521/p/11602990.html