降维实际上就是降低特征的个数,最终的结果就是特征和特征之间不相关。
降维:降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程
定义:数据中包含冗余或相关变量(或称为特征、属性、指标等),旨在从原有特征中找出主要特征Filter(过滤式):主要探究特征本身特点、特征与特征和目标值之间关联。
方差选择法:低方差特征过滤.例如鸟类是否可以飞作为特征值是不合适的,此时的方差为0
相关系数:目的是去除冗余,确定特征与特征之间的相关性
Embedded(嵌入式):算法自动选择特征(特征与目标值之间的关联)
决策树:信息熵、信息增益
正则化:L1、L2
深度学习:卷积等sklearn.feature_selection删除低方差的一些特征,从方差的大小来考虑方式的角度。
特征方差小:某个特征大多样本的值比较相近
特征方差大:某个特征很多样本的值有比较有差别sklearn.feature_selection.VarianceThreshold( threshold = 0.0 )
删除所有低方差特征
Variance.fit_transform(X)
X:numpy array格式的数据 [n_samples, n_features]
返回:训练集差异低于 threshold的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。#删除低方差特征Demo from sklearn.datasets import load_iris from sklearn.feature_selection import VarianceThreshold import pandas as pd def variance_demo(): iris = load_iris() data = pd.DataFrame(iris.data, columns = iris.feature_names) data_new = data.iloc[:, :4].values print("data_new:\n", data_new) transfer = VarianceThreshold(threshold = 0.5) data_variance_value = transfer.fit_transform(data_new) print("data_variance_value:\n", data_variance_value) return None if __name__ == ‘__main__‘: variance_demo() 输出结果: data_new: [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2] [5.4 3.9 1.7 0.4] [4.6 3.4 1.4 0.3] [5. 3.4 1.5 0.2] [4.4 2.9 1.4 0.2] [4.9 3.1 1.5 0.1] [5.4 3.7 1.5 0.2] [4.8 3.4 1.6 0.2] [4.8 3. 1.4 0.1] [4.3 3. 1.1 0.1] [5.8 4. 1.2 0.2] [5.7 4.4 1.5 0.4] [5.4 3.9 1.3 0.4] [5.1 3.5 1.4 0.3] [5.7 3.8 1.7 0.3] [5.1 3.8 1.5 0.3] [5.4 3.4 1.7 0.2] [5.1 3.7 1.5 0.4] [4.6 3.6 1. 0.2] [5.1 3.3 1.7 0.5] [4.8 3.4 1.9 0.2] [5. 3. 1.6 0.2] [5. 3.4 1.6 0.4] [5.2 3.5 1.5 0.2] [5.2 3.4 1.4 0.2] [4.7 3.2 1.6 0.2] [4.8 3.1 1.6 0.2] [5.4 3.4 1.5 0.4] [5.2 4.1 1.5 0.1] [5.5 4.2 1.4 0.2] [4.9 3.1 1.5 0.1] [5. 3.2 1.2 0.2] [5.5 3.5 1.3 0.2] [4.9 3.1 1.5 0.1] [4.4 3. 1.3 0.2] [5.1 3.4 1.5 0.2] [5. 3.5 1.3 0.3] [4.5 2.3 1.3 0.3] [4.4 3.2 1.3 0.2] [5. 3.5 1.6 0.6] [5.1 3.8 1.9 0.4] [4.8 3. 1.4 0.3] [5.1 3.8 1.6 0.2] [4.6 3.2 1.4 0.2] [5.3 3.7 1.5 0.2] [5. 3.3 1.4 0.2] [7. 3.2 4.7 1.4] [6.4 3.2 4.5 1.5] [6.9 3.1 4.9 1.5] [5.5 2.3 4. 1.3] [6.5 2.8 4.6 1.5] [5.7 2.8 4.5 1.3] [6.3 3.3 4.7 1.6] [4.9 2.4 3.3 1. ] [6.6 2.9 4.6 1.3] [5.2 2.7 3.9 1.4] [5. 2. 3.5 1. ] [5.9 3. 4.2 1.5] [6. 2.2 4. 1. ] [6.1 2.9 4.7 1.4] [5.6 2.9 3.6 1.3] [6.7 3.1 4.4 1.4] [5.6 3. 4.5 1.5] [5.8 2.7 4.1 1. ] [6.2 2.2 4.5 1.5] [5.6 2.5 3.9 1.1] [5.9 3.2 4.8 1.8] [6.1 2.8 4. 1.3] [6.3 2.5 4.9 1.5] [6.1 2.8 4.7 1.2] [6.4 2.9 4.3 1.3] [6.6 3. 4.4 1.4] [6.8 2.8 4.8 1.4] [6.7 3. 5. 1.7] [6. 2.9 4.5 1.5] [5.7 2.6 3.5 1. ] [5.5 2.4 3.8 1.1] [5.5 2.4 3.7 1. ] [5.8 2.7 3.9 1.2] [6. 2.7 5.1 1.6] [5.4 3. 4.5 1.5] [6. 3.4 4.5 1.6] [6.7 3.1 4.7 1.5] [6.3 2.3 4.4 1.3] [5.6 3. 4.1 1.3] [5.5 2.5 4. 1.3] [5.5 2.6 4.4 1.2] [6.1 3. 4.6 1.4] [5.8 2.6 4. 1.2] [5. 2.3 3.3 1. ] [5.6 2.7 4.2 1.3] [5.7 3. 4.2 1.2] [5.7 2.9 4.2 1.3] [6.2 2.9 4.3 1.3] [5.1 2.5 3. 1.1] [5.7 2.8 4.1 1.3] [6.3 3.3 6. 2.5] [5.8 2.7 5.1 1.9] [7.1 3. 5.9 2.1] [6.3 2.9 5.6 1.8] [6.5 3. 5.8 2.2] [7.6 3. 6.6 2.1] [4.9 2.5 4.5 1.7] [7.3 2.9 6.3 1.8] [6.7 2.5 5.8 1.8] [7.2 3.6 6.1 2.5] [6.5 3.2 5.1 2. ] [6.4 2.7 5.3 1.9] [6.8 3. 5.5 2.1] [5.7 2.5 5. 2. ] [5.8 2.8 5.1 2.4] [6.4 3.2 5.3 2.3] [6.5 3. 5.5 1.8] [7.7 3.8 6.7 2.2] [7.7 2.6 6.9 2.3] [6. 2.2 5. 1.5] [6.9 3.2 5.7 2.3] [5.6 2.8 4.9 2. ] [7.7 2.8 6.7 2. ] [6.3 2.7 4.9 1.8] [6.7 3.3 5.7 2.1] [7.2 3.2 6. 1.8] [6.2 2.8 4.8 1.8] [6.1 3. 4.9 1.8] [6.4 2.8 5.6 2.1] [7.2 3. 5.8 1.6] [7.4 2.8 6.1 1.9] [7.9 3.8 6.4 2. ] [6.4 2.8 5.6 2.2] [6.3 2.8 5.1 1.5] [6.1 2.6 5.6 1.4] [7.7 3. 6.1 2.3] [6.3 3.4 5.6 2.4] [6.4 3.1 5.5 1.8] [6. 3. 4.8 1.8] [6.9 3.1 5.4 2.1] [6.7 3.1 5.6 2.4] [6.9 3.1 5.1 2.3] [5.8 2.7 5.1 1.9] [6.8 3.2 5.9 2.3] [6.7 3.3 5.7 2.5] [6.7 3. 5.2 2.3] [6.3 2.5 5. 1.9] [6.5 3. 5.2 2. ] [6.2 3.4 5.4 2.3] [5.9 3. 5.1 1.8]] data_variance_value: [[5.1 1.4 0.2] [4.9 1.4 0.2] [4.7 1.3 0.2] [4.6 1.5 0.2] [5. 1.4 0.2] [5.4 1.7 0.4] [4.6 1.4 0.3] [5. 1.5 0.2] [4.4 1.4 0.2] [4.9 1.5 0.1] [5.4 1.5 0.2] [4.8 1.6 0.2] [4.8 1.4 0.1] [4.3 1.1 0.1] [5.8 1.2 0.2] [5.7 1.5 0.4] [5.4 1.3 0.4] [5.1 1.4 0.3] [5.7 1.7 0.3] [5.1 1.5 0.3] [5.4 1.7 0.2] [5.1 1.5 0.4] [4.6 1. 0.2] [5.1 1.7 0.5] [4.8 1.9 0.2] [5. 1.6 0.2] [5. 1.6 0.4] [5.2 1.5 0.2] [5.2 1.4 0.2] [4.7 1.6 0.2] [4.8 1.6 0.2] [5.4 1.5 0.4] [5.2 1.5 0.1] [5.5 1.4 0.2] [4.9 1.5 0.1] [5. 1.2 0.2] [5.5 1.3 0.2] [4.9 1.5 0.1] [4.4 1.3 0.2] [5.1 1.5 0.2] [5. 1.3 0.3] [4.5 1.3 0.3] [4.4 1.3 0.2] [5. 1.6 0.6] [5.1 1.9 0.4] [4.8 1.4 0.3] [5.1 1.6 0.2] [4.6 1.4 0.2] [5.3 1.5 0.2] [5. 1.4 0.2] [7. 4.7 1.4] [6.4 4.5 1.5] [6.9 4.9 1.5] [5.5 4. 1.3] [6.5 4.6 1.5] [5.7 4.5 1.3] [6.3 4.7 1.6] [4.9 3.3 1. ] [6.6 4.6 1.3] [5.2 3.9 1.4] [5. 3.5 1. ] [5.9 4.2 1.5] [6. 4. 1. ] [6.1 4.7 1.4] [5.6 3.6 1.3] [6.7 4.4 1.4] [5.6 4.5 1.5] [5.8 4.1 1. ] [6.2 4.5 1.5] [5.6 3.9 1.1] [5.9 4.8 1.8] [6.1 4. 1.3] [6.3 4.9 1.5] [6.1 4.7 1.2] [6.4 4.3 1.3] [6.6 4.4 1.4] [6.8 4.8 1.4] [6.7 5. 1.7] [6. 4.5 1.5] [5.7 3.5 1. ] [5.5 3.8 1.1] [5.5 3.7 1. ] [5.8 3.9 1.2] [6. 5.1 1.6] [5.4 4.5 1.5] [6. 4.5 1.6] [6.7 4.7 1.5] [6.3 4.4 1.3] [5.6 4.1 1.3] [5.5 4. 1.3] [5.5 4.4 1.2] [6.1 4.6 1.4] [5.8 4. 1.2] [5. 3.3 1. ] [5.6 4.2 1.3] [5.7 4.2 1.2] [5.7 4.2 1.3] [6.2 4.3 1.3] [5.1 3. 1.1] [5.7 4.1 1.3] [6.3 6. 2.5] [5.8 5.1 1.9] [7.1 5.9 2.1] [6.3 5.6 1.8] [6.5 5.8 2.2] [7.6 6.6 2.1] [4.9 4.5 1.7] [7.3 6.3 1.8] [6.7 5.8 1.8] [7.2 6.1 2.5] [6.5 5.1 2. ] [6.4 5.3 1.9] [6.8 5.5 2.1] [5.7 5. 2. ] [5.8 5.1 2.4] [6.4 5.3 2.3] [6.5 5.5 1.8] [7.7 6.7 2.2] [7.7 6.9 2.3] [6. 5. 1.5] [6.9 5.7 2.3] [5.6 4.9 2. ] [7.7 6.7 2. ] [6.3 4.9 1.8] [6.7 5.7 2.1] [7.2 6. 1.8] [6.2 4.8 1.8] [6.1 4.9 1.8] [6.4 5.6 2.1] [7.2 5.8 1.6] [7.4 6.1 1.9] [7.9 6.4 2. ] [6.4 5.6 2.2] [6.3 5.1 1.5] [6.1 5.6 1.4] [7.7 6.1 2.3] [6.3 5.6 2.4] [6.4 5.5 1.8] [6. 4.8 1.8] [6.9 5.4 2.1] [6.7 5.6 2.4] [6.9 5.1 2.3] [5.8 5.1 1.9] [6.8 5.9 2.3] [6.7 5.7 2.5] [6.7 5.2 2.3] [6.3 5. 1.9] [6.5 5.2 2. ] [6.2 5.4 2.3] [5.9 5.1 1.8]]
皮尔森相关系数
反映变量之间相关关系密切程度的统计指标
公式:(在此不列出来了,可以在网上百度一下,了解一下即可)
相关系数的值介于-1与+1之间,即-1≤r≤+1。其性质如下:
当r>0时,表示两变量正相关,r<0时,两变量为负相关
当r=|1|时,表示两变量为完全相关,当r=0时,表示狼变量无相关关系
当0<|r|<1时,表示两变量存在一定程度的相关,|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
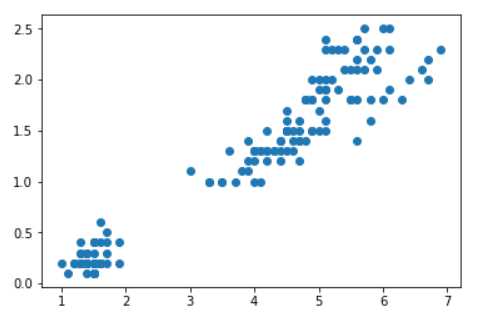
一般可按三级划分:|r|<0.4为低度相关;0.4≤|r|<0.7为显著相关;0.7≤|r|<1为高度线性相关from scipy.stats import pearsonr#过滤低方差特征 + 计算相关系数DEMO #皮尔森相关系数,计算特征与目标变量之间的相关度 from scipy.stats import pearsonr from sklearn.datasets import load_iris from sklearn.feature_selection import VarianceThreshold import pandas as pd def variance_demo(): iris = load_iris() data = pd.DataFrame(iris.data, columns = [‘sepal length‘, ‘sepal width‘, ‘petal length‘, ‘petal width‘]) data_new = data.iloc[:, :4].values print("data_new:\n", data_new) transfer = VarianceThreshold(threshold = 0.5) data_variance_value = transfer.fit_transform(data_new) print("data_variance_value:\n", data_variance_value) #计算两个变量之间的相关系数 r1 = pearsonr(data[‘sepal length‘], data[‘petal length‘]) print("sepal length与petal length的相关系数:\n", r1) r2 = pearsonr(data[‘petal length‘], data[‘petal width‘]) print("petal length与petal width的相关系数:\n", r2) import matplotlib.pyplot as plt plt.scatter(data[‘petal length‘], data[‘petal width‘]) plt.show() return None if __name__ == ‘__main__‘: variance_demo() 输出结果: data_new: [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2] [5.4 3.9 1.7 0.4] [4.6 3.4 1.4 0.3] [5. 3.4 1.5 0.2] [4.4 2.9 1.4 0.2] [4.9 3.1 1.5 0.1] [5.4 3.7 1.5 0.2] [4.8 3.4 1.6 0.2] [4.8 3. 1.4 0.1] [4.3 3. 1.1 0.1] [5.8 4. 1.2 0.2] [5.7 4.4 1.5 0.4] [5.4 3.9 1.3 0.4] [5.1 3.5 1.4 0.3] [5.7 3.8 1.7 0.3] [5.1 3.8 1.5 0.3] [5.4 3.4 1.7 0.2] [5.1 3.7 1.5 0.4] [4.6 3.6 1. 0.2] [5.1 3.3 1.7 0.5] [4.8 3.4 1.9 0.2] [5. 3. 1.6 0.2] [5. 3.4 1.6 0.4] [5.2 3.5 1.5 0.2] [5.2 3.4 1.4 0.2] [4.7 3.2 1.6 0.2] [4.8 3.1 1.6 0.2] [5.4 3.4 1.5 0.4] [5.2 4.1 1.5 0.1] [5.5 4.2 1.4 0.2] [4.9 3.1 1.5 0.1] [5. 3.2 1.2 0.2] [5.5 3.5 1.3 0.2] [4.9 3.1 1.5 0.1] [4.4 3. 1.3 0.2] [5.1 3.4 1.5 0.2] [5. 3.5 1.3 0.3] [4.5 2.3 1.3 0.3] [4.4 3.2 1.3 0.2] [5. 3.5 1.6 0.6] [5.1 3.8 1.9 0.4] [4.8 3. 1.4 0.3] [5.1 3.8 1.6 0.2] [4.6 3.2 1.4 0.2] [5.3 3.7 1.5 0.2] [5. 3.3 1.4 0.2] [7. 3.2 4.7 1.4] [6.4 3.2 4.5 1.5] [6.9 3.1 4.9 1.5] [5.5 2.3 4. 1.3] [6.5 2.8 4.6 1.5] [5.7 2.8 4.5 1.3] [6.3 3.3 4.7 1.6] [4.9 2.4 3.3 1. ] [6.6 2.9 4.6 1.3] [5.2 2.7 3.9 1.4] [5. 2. 3.5 1. ] [5.9 3. 4.2 1.5] [6. 2.2 4. 1. ] [6.1 2.9 4.7 1.4] [5.6 2.9 3.6 1.3] [6.7 3.1 4.4 1.4] [5.6 3. 4.5 1.5] [5.8 2.7 4.1 1. ] [6.2 2.2 4.5 1.5] [5.6 2.5 3.9 1.1] [5.9 3.2 4.8 1.8] [6.1 2.8 4. 1.3] [6.3 2.5 4.9 1.5] [6.1 2.8 4.7 1.2] [6.4 2.9 4.3 1.3] [6.6 3. 4.4 1.4] [6.8 2.8 4.8 1.4] [6.7 3. 5. 1.7] [6. 2.9 4.5 1.5] [5.7 2.6 3.5 1. ] [5.5 2.4 3.8 1.1] [5.5 2.4 3.7 1. ] [5.8 2.7 3.9 1.2] [6. 2.7 5.1 1.6] [5.4 3. 4.5 1.5] [6. 3.4 4.5 1.6] [6.7 3.1 4.7 1.5] [6.3 2.3 4.4 1.3] [5.6 3. 4.1 1.3] [5.5 2.5 4. 1.3] [5.5 2.6 4.4 1.2] [6.1 3. 4.6 1.4] [5.8 2.6 4. 1.2] [5. 2.3 3.3 1. ] [5.6 2.7 4.2 1.3] [5.7 3. 4.2 1.2] [5.7 2.9 4.2 1.3] [6.2 2.9 4.3 1.3] [5.1 2.5 3. 1.1] [5.7 2.8 4.1 1.3] [6.3 3.3 6. 2.5] [5.8 2.7 5.1 1.9] [7.1 3. 5.9 2.1] [6.3 2.9 5.6 1.8] [6.5 3. 5.8 2.2] [7.6 3. 6.6 2.1] [4.9 2.5 4.5 1.7] [7.3 2.9 6.3 1.8] [6.7 2.5 5.8 1.8] [7.2 3.6 6.1 2.5] [6.5 3.2 5.1 2. ] [6.4 2.7 5.3 1.9] [6.8 3. 5.5 2.1] [5.7 2.5 5. 2. ] [5.8 2.8 5.1 2.4] [6.4 3.2 5.3 2.3] [6.5 3. 5.5 1.8] [7.7 3.8 6.7 2.2] [7.7 2.6 6.9 2.3] [6. 2.2 5. 1.5] [6.9 3.2 5.7 2.3] [5.6 2.8 4.9 2. ] [7.7 2.8 6.7 2. ] [6.3 2.7 4.9 1.8] [6.7 3.3 5.7 2.1] [7.2 3.2 6. 1.8] [6.2 2.8 4.8 1.8] [6.1 3. 4.9 1.8] [6.4 2.8 5.6 2.1] [7.2 3. 5.8 1.6] [7.4 2.8 6.1 1.9] [7.9 3.8 6.4 2. ] [6.4 2.8 5.6 2.2] [6.3 2.8 5.1 1.5] [6.1 2.6 5.6 1.4] [7.7 3. 6.1 2.3] [6.3 3.4 5.6 2.4] [6.4 3.1 5.5 1.8] [6. 3. 4.8 1.8] [6.9 3.1 5.4 2.1] [6.7 3.1 5.6 2.4] [6.9 3.1 5.1 2.3] [5.8 2.7 5.1 1.9] [6.8 3.2 5.9 2.3] [6.7 3.3 5.7 2.5] [6.7 3. 5.2 2.3] [6.3 2.5 5. 1.9] [6.5 3. 5.2 2. ] [6.2 3.4 5.4 2.3] [5.9 3. 5.1 1.8]] data_variance_value: [[5.1 1.4 0.2] [4.9 1.4 0.2] [4.7 1.3 0.2] [4.6 1.5 0.2] [5. 1.4 0.2] [5.4 1.7 0.4] [4.6 1.4 0.3] [5. 1.5 0.2] [4.4 1.4 0.2] [4.9 1.5 0.1] [5.4 1.5 0.2] [4.8 1.6 0.2] [4.8 1.4 0.1] [4.3 1.1 0.1] [5.8 1.2 0.2] [5.7 1.5 0.4] [5.4 1.3 0.4] [5.1 1.4 0.3] [5.7 1.7 0.3] [5.1 1.5 0.3] [5.4 1.7 0.2] [5.1 1.5 0.4] [4.6 1. 0.2] [5.1 1.7 0.5] [4.8 1.9 0.2] [5. 1.6 0.2] [5. 1.6 0.4] [5.2 1.5 0.2] [5.2 1.4 0.2] [4.7 1.6 0.2] [4.8 1.6 0.2] [5.4 1.5 0.4] [5.2 1.5 0.1] [5.5 1.4 0.2] [4.9 1.5 0.1] [5. 1.2 0.2] [5.5 1.3 0.2] [4.9 1.5 0.1] [4.4 1.3 0.2] [5.1 1.5 0.2] [5. 1.3 0.3] [4.5 1.3 0.3] [4.4 1.3 0.2] [5. 1.6 0.6] [5.1 1.9 0.4] [4.8 1.4 0.3] [5.1 1.6 0.2] [4.6 1.4 0.2] [5.3 1.5 0.2] [5. 1.4 0.2] [7. 4.7 1.4] [6.4 4.5 1.5] [6.9 4.9 1.5] [5.5 4. 1.3] [6.5 4.6 1.5] [5.7 4.5 1.3] [6.3 4.7 1.6] [4.9 3.3 1. ] [6.6 4.6 1.3] [5.2 3.9 1.4] [5. 3.5 1. ] [5.9 4.2 1.5] [6. 4. 1. ] [6.1 4.7 1.4] [5.6 3.6 1.3] [6.7 4.4 1.4] [5.6 4.5 1.5] [5.8 4.1 1. ] [6.2 4.5 1.5] [5.6 3.9 1.1] [5.9 4.8 1.8] [6.1 4. 1.3] [6.3 4.9 1.5] [6.1 4.7 1.2] [6.4 4.3 1.3] [6.6 4.4 1.4] [6.8 4.8 1.4] [6.7 5. 1.7] [6. 4.5 1.5] [5.7 3.5 1. ] [5.5 3.8 1.1] [5.5 3.7 1. ] [5.8 3.9 1.2] [6. 5.1 1.6] [5.4 4.5 1.5] [6. 4.5 1.6] [6.7 4.7 1.5] [6.3 4.4 1.3] [5.6 4.1 1.3] [5.5 4. 1.3] [5.5 4.4 1.2] [6.1 4.6 1.4] [5.8 4. 1.2] [5. 3.3 1. ] [5.6 4.2 1.3] [5.7 4.2 1.2] [5.7 4.2 1.3] [6.2 4.3 1.3] [5.1 3. 1.1] [5.7 4.1 1.3] [6.3 6. 2.5] [5.8 5.1 1.9] [7.1 5.9 2.1] [6.3 5.6 1.8] [6.5 5.8 2.2] [7.6 6.6 2.1] [4.9 4.5 1.7] [7.3 6.3 1.8] [6.7 5.8 1.8] [7.2 6.1 2.5] [6.5 5.1 2. ] [6.4 5.3 1.9] [6.8 5.5 2.1] [5.7 5. 2. ] [5.8 5.1 2.4] [6.4 5.3 2.3] [6.5 5.5 1.8] [7.7 6.7 2.2] [7.7 6.9 2.3] [6. 5. 1.5] [6.9 5.7 2.3] [5.6 4.9 2. ] [7.7 6.7 2. ] [6.3 4.9 1.8] [6.7 5.7 2.1] [7.2 6. 1.8] [6.2 4.8 1.8] [6.1 4.9 1.8] [6.4 5.6 2.1] [7.2 5.8 1.6] [7.4 6.1 1.9] [7.9 6.4 2. ] [6.4 5.6 2.2] [6.3 5.1 1.5] [6.1 5.6 1.4] [7.7 6.1 2.3] [6.3 5.6 2.4] [6.4 5.5 1.8] [6. 4.8 1.8] [6.9 5.4 2.1] [6.7 5.6 2.4] [6.9 5.1 2.3] [5.8 5.1 1.9] [6.8 5.9 2.3] [6.7 5.7 2.5] [6.7 5.2 2.3] [6.3 5. 1.9] [6.5 5.2 2. ] [6.2 5.4 2.3] [5.9 5.1 1.8]] sepal length与petal length的相关系数: (0.8717541573048712, 1.0384540627941809e-47) petal length与petal width的相关系数: (0.9627570970509662, 5.776660988495158e-86)
1)选取其中一个
2)加权求和
3)主成分分析在所有特征选择方法,方差,SelectKBest+各种统计量(卡方过滤、F检验、互信息法),嵌入法和包装法,都有接口get_support,该接口有参数indices,get_support(indices=False),参数为false的时候可以用来确定原特征矩阵中有哪些特征被选择出来,返回布尔值True或者False,如果设定indices=True,就可以确定被选择出来的特征在原特征矩阵中所在的位置的索引。
X_train_columns = X_train.columns
selector = VarianceThreshold(0.005071)
X_fsvar = selector.fit_transform(X_train)
X_fsvar.columns = X_train_columns[selector.get_support(indices=True)]定义:高维数据转化为地位数据的过程,在此过程中可能会舍弃原有数据、创造新的变量
作用:是数据维数的压缩,尽可能降低原数据的维数(复杂度),损失少量信息
应用:回归分析或者据类分析当中sklearn.decomposition.PCA(n_components = None)
将数据分解为较低维数空间
n_components:
小数:表示包留百分之多少的信息
整数:减少到多少特征
PCA.fit_transform(X)
X:numpy array格式的数据[n_samples, n_features]
返回:转换后指定维度的arrayfrom sklearn.decomposition import PCA from sklearn.datasets import load_iris import pandas as pd def pca_demo(): iris = load_iris() data = pd.DataFrame(iris.data, columns = iris.feature_names) data_array = data.iloc[:, :4].values print("data_array:\n", data_array) transfer = PCA(n_components = 2) #ransfer = PCA(n_components = 0.95) data_pca_value = transfer.fit_transform(data_array) print("data_pca_value:\n", data_pca_value) return None if __name__ == ‘__main__‘: pca_demo() 输出结果: data_array: [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2] [5.4 3.9 1.7 0.4] [4.6 3.4 1.4 0.3] [5. 3.4 1.5 0.2] [4.4 2.9 1.4 0.2] [4.9 3.1 1.5 0.1] [5.4 3.7 1.5 0.2] [4.8 3.4 1.6 0.2] [4.8 3. 1.4 0.1] [4.3 3. 1.1 0.1] [5.8 4. 1.2 0.2] [5.7 4.4 1.5 0.4] [5.4 3.9 1.3 0.4] [5.1 3.5 1.4 0.3] [5.7 3.8 1.7 0.3] [5.1 3.8 1.5 0.3] [5.4 3.4 1.7 0.2] [5.1 3.7 1.5 0.4] [4.6 3.6 1. 0.2] [5.1 3.3 1.7 0.5] [4.8 3.4 1.9 0.2] [5. 3. 1.6 0.2] [5. 3.4 1.6 0.4] [5.2 3.5 1.5 0.2] [5.2 3.4 1.4 0.2] [4.7 3.2 1.6 0.2] [4.8 3.1 1.6 0.2] [5.4 3.4 1.5 0.4] [5.2 4.1 1.5 0.1] [5.5 4.2 1.4 0.2] [4.9 3.1 1.5 0.1] [5. 3.2 1.2 0.2] [5.5 3.5 1.3 0.2] [4.9 3.1 1.5 0.1] [4.4 3. 1.3 0.2] [5.1 3.4 1.5 0.2] [5. 3.5 1.3 0.3] [4.5 2.3 1.3 0.3] [4.4 3.2 1.3 0.2] [5. 3.5 1.6 0.6] [5.1 3.8 1.9 0.4] [4.8 3. 1.4 0.3] [5.1 3.8 1.6 0.2] [4.6 3.2 1.4 0.2] [5.3 3.7 1.5 0.2] [5. 3.3 1.4 0.2] [7. 3.2 4.7 1.4] [6.4 3.2 4.5 1.5] [6.9 3.1 4.9 1.5] [5.5 2.3 4. 1.3] [6.5 2.8 4.6 1.5] [5.7 2.8 4.5 1.3] [6.3 3.3 4.7 1.6] [4.9 2.4 3.3 1. ] [6.6 2.9 4.6 1.3] [5.2 2.7 3.9 1.4] [5. 2. 3.5 1. ] [5.9 3. 4.2 1.5] [6. 2.2 4. 1. ] [6.1 2.9 4.7 1.4] [5.6 2.9 3.6 1.3] [6.7 3.1 4.4 1.4] [5.6 3. 4.5 1.5] [5.8 2.7 4.1 1. ] [6.2 2.2 4.5 1.5] [5.6 2.5 3.9 1.1] [5.9 3.2 4.8 1.8] [6.1 2.8 4. 1.3] [6.3 2.5 4.9 1.5] [6.1 2.8 4.7 1.2] [6.4 2.9 4.3 1.3] [6.6 3. 4.4 1.4] [6.8 2.8 4.8 1.4] [6.7 3. 5. 1.7] [6. 2.9 4.5 1.5] [5.7 2.6 3.5 1. ] [5.5 2.4 3.8 1.1] [5.5 2.4 3.7 1. ] [5.8 2.7 3.9 1.2] [6. 2.7 5.1 1.6] [5.4 3. 4.5 1.5] [6. 3.4 4.5 1.6] [6.7 3.1 4.7 1.5] [6.3 2.3 4.4 1.3] [5.6 3. 4.1 1.3] [5.5 2.5 4. 1.3] [5.5 2.6 4.4 1.2] [6.1 3. 4.6 1.4] [5.8 2.6 4. 1.2] [5. 2.3 3.3 1. ] [5.6 2.7 4.2 1.3] [5.7 3. 4.2 1.2] [5.7 2.9 4.2 1.3] [6.2 2.9 4.3 1.3] [5.1 2.5 3. 1.1] [5.7 2.8 4.1 1.3] [6.3 3.3 6. 2.5] [5.8 2.7 5.1 1.9] [7.1 3. 5.9 2.1] [6.3 2.9 5.6 1.8] [6.5 3. 5.8 2.2] [7.6 3. 6.6 2.1] [4.9 2.5 4.5 1.7] [7.3 2.9 6.3 1.8] [6.7 2.5 5.8 1.8] [7.2 3.6 6.1 2.5] [6.5 3.2 5.1 2. ] [6.4 2.7 5.3 1.9] [6.8 3. 5.5 2.1] [5.7 2.5 5. 2. ] [5.8 2.8 5.1 2.4] [6.4 3.2 5.3 2.3] [6.5 3. 5.5 1.8] [7.7 3.8 6.7 2.2] [7.7 2.6 6.9 2.3] [6. 2.2 5. 1.5] [6.9 3.2 5.7 2.3] [5.6 2.8 4.9 2. ] [7.7 2.8 6.7 2. ] [6.3 2.7 4.9 1.8] [6.7 3.3 5.7 2.1] [7.2 3.2 6. 1.8] [6.2 2.8 4.8 1.8] [6.1 3. 4.9 1.8] [6.4 2.8 5.6 2.1] [7.2 3. 5.8 1.6] [7.4 2.8 6.1 1.9] [7.9 3.8 6.4 2. ] [6.4 2.8 5.6 2.2] [6.3 2.8 5.1 1.5] [6.1 2.6 5.6 1.4] [7.7 3. 6.1 2.3] [6.3 3.4 5.6 2.4] [6.4 3.1 5.5 1.8] [6. 3. 4.8 1.8] [6.9 3.1 5.4 2.1] [6.7 3.1 5.6 2.4] [6.9 3.1 5.1 2.3] [5.8 2.7 5.1 1.9] [6.8 3.2 5.9 2.3] [6.7 3.3 5.7 2.5] [6.7 3. 5.2 2.3] [6.3 2.5 5. 1.9] [6.5 3. 5.2 2. ] [6.2 3.4 5.4 2.3] [5.9 3. 5.1 1.8]] data_pca_value: [[-2.68420713 0.32660731] [-2.71539062 -0.16955685] [-2.88981954 -0.13734561] [-2.7464372 -0.31112432] [-2.72859298 0.33392456] [-2.27989736 0.74778271] [-2.82089068 -0.08210451] [-2.62648199 0.17040535] [-2.88795857 -0.57079803] [-2.67384469 -0.1066917 ] [-2.50652679 0.65193501] [-2.61314272 0.02152063] [-2.78743398 -0.22774019] [-3.22520045 -0.50327991] [-2.64354322 1.1861949 ] [-2.38386932 1.34475434] [-2.6225262 0.81808967] [-2.64832273 0.31913667] [-2.19907796 0.87924409] [-2.58734619 0.52047364] [-2.3105317 0.39786782] [-2.54323491 0.44003175] [-3.21585769 0.14161557] [-2.30312854 0.10552268] [-2.35617109 -0.03120959] [-2.50791723 -0.13905634] [-2.469056 0.13788731] [-2.56239095 0.37468456] [-2.63982127 0.31929007] [-2.63284791 -0.19007583] [-2.58846205 -0.19739308] [-2.41007734 0.41808001] [-2.64763667 0.81998263] [-2.59715948 1.10002193] [-2.67384469 -0.1066917 ] [-2.86699985 0.0771931 ] [-2.62522846 0.60680001] [-2.67384469 -0.1066917 ] [-2.98184266 -0.48025005] [-2.59032303 0.23605934] [-2.77013891 0.27105942] [-2.85221108 -0.93286537] [-2.99829644 -0.33430757] [-2.4055141 0.19591726] [-2.20883295 0.44269603] [-2.71566519 -0.24268148] [-2.53757337 0.51036755] [-2.8403213 -0.22057634] [-2.54268576 0.58628103] [-2.70391231 0.11501085] [ 1.28479459 0.68543919] [ 0.93241075 0.31919809] [ 1.46406132 0.50418983] [ 0.18096721 -0.82560394] [ 1.08713449 0.07539039] [ 0.64043675 -0.41732348] [ 1.09522371 0.28389121] [-0.75146714 -1.00110751] [ 1.04329778 0.22895691] [-0.01019007 -0.72057487] [-0.5110862 -1.26249195] [ 0.51109806 -0.10228411] [ 0.26233576 -0.5478933 ] [ 0.98404455 -0.12436042] [-0.174864 -0.25181557] [ 0.92757294 0.46823621] [ 0.65959279 -0.35197629] [ 0.23454059 -0.33192183] [ 0.94236171 -0.54182226] [ 0.0432464 -0.58148945] [ 1.11624072 -0.08421401] [ 0.35678657 -0.06682383] [ 1.29646885 -0.32756152] [ 0.92050265 -0.18239036] [ 0.71400821 0.15037915] [ 0.89964086 0.32961098] [ 1.33104142 0.24466952] [ 1.55739627 0.26739258] [ 0.81245555 -0.16233157] [-0.30733476 -0.36508661] [-0.07034289 -0.70253793] [-0.19188449 -0.67749054] [ 0.13499495 -0.31170964] [ 1.37873698 -0.42120514] [ 0.58727485 -0.48328427] [ 0.8072055 0.19505396] [ 1.22042897 0.40803534] [ 0.81286779 -0.370679 ] [ 0.24519516 -0.26672804] [ 0.16451343 -0.67966147] [ 0.46303099 -0.66952655] [ 0.89016045 -0.03381244] [ 0.22887905 -0.40225762] [-0.70708128 -1.00842476] [ 0.35553304 -0.50321849] [ 0.33112695 -0.21118014] [ 0.37523823 -0.29162202] [ 0.64169028 0.01907118] [-0.90846333 -0.75156873] [ 0.29780791 -0.34701652] [ 2.53172698 -0.01184224] [ 1.41407223 -0.57492506] [ 2.61648461 0.34193529] [ 1.97081495 -0.18112569] [ 2.34975798 -0.04188255] [ 3.39687992 0.54716805] [ 0.51938325 -1.19135169] [ 2.9320051 0.35237701] [ 2.31967279 -0.24554817] [ 2.91813423 0.78038063] [ 1.66193495 0.2420384 ] [ 1.80234045 -0.21615461] [ 2.16537886 0.21528028] [ 1.34459422 -0.77641543] [ 1.5852673 -0.53930705] [ 1.90474358 0.11881899] [ 1.94924878 0.04073026] [ 3.48876538 1.17154454] [ 3.79468686 0.25326557] [ 1.29832982 -0.76101394] [ 2.42816726 0.37678197] [ 1.19809737 -0.60557896] [ 3.49926548 0.45677347] [ 1.38766825 -0.20403099] [ 2.27585365 0.33338653] [ 2.61419383 0.55836695] [ 1.25762518 -0.179137 ] [ 1.29066965 -0.11642525] [ 2.12285398 -0.21085488] [ 2.3875644 0.46251925] [ 2.84096093 0.37274259] [ 3.2323429 1.37052404] [ 2.15873837 -0.21832553] [ 1.4431026 -0.14380129] [ 1.77964011 -0.50146479] [ 3.07652162 0.68576444] [ 2.14498686 0.13890661] [ 1.90486293 0.04804751] [ 1.16885347 -0.1645025 ] [ 2.10765373 0.37148225] [ 2.31430339 0.18260885] [ 1.92245088 0.40927118] [ 1.41407223 -0.57492506] [ 2.56332271 0.2759745 ] [ 2.41939122 0.30350394] [ 1.94401705 0.18741522] [ 1.52566363 -0.37502085] [ 1.76404594 0.07851919] [ 1.90162908 0.11587675] [ 1.38966613 -0.28288671]]
参考链接:https://www.cnblogs.com/ftl1012/p/10498480.html
原文:https://www.cnblogs.com/henabo/p/11603034.html