1. 题目描述

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.
Note：
1. there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].
2. You may assume all tickets form at least one valid itinerary.

Example 1:
Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]
Example 2:
Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"]. But it is larger in lexical order.

2. 题目理解

将上述的问题用图的形式表示出来
对于Example1，表示为：

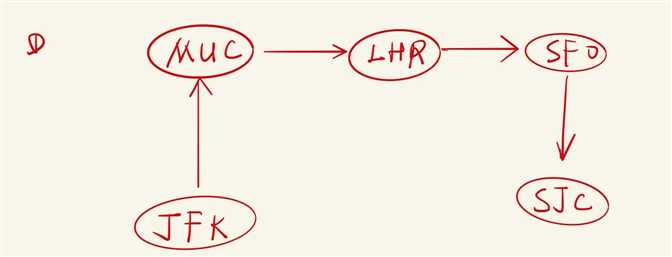
可以看到只有一条可以从JFK一次用光全部Tickets的方案
对于Example2，表示为：

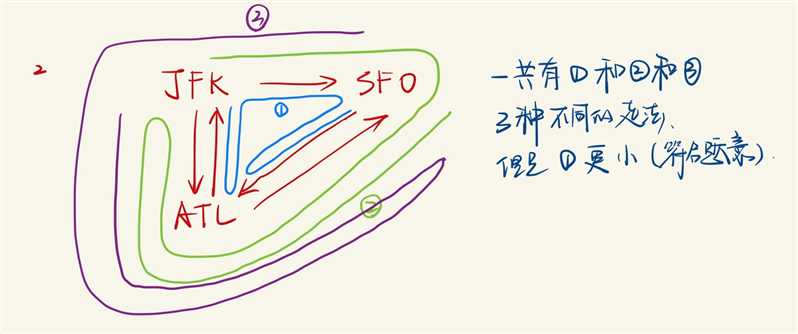
可以看到，3个可能的路径中，1??最小，符合要求。

3. 题目分析

根据题目的理解，分析找到路径1的过程：
我们从JFK出发：

1. 当前节点为JFK，当前节点可前往的可选列表为[ATL, SFO]，根据字符串序列最小化的原则，我们从可选列表中选取字符串最小的ATL，同时，下次经过JFK时候，由于ATL已经用过了，因此现在也要将ATL从JFK的待选择列表中删除。
2. 当前节点变为ATL，同时其可前往节点的可选列表为[JFK, SFO]，选择JFK，并从ATL的可选列表中删除JFK。
3. 当前节点变为JFK，其可前往节点的可选列表为[SFO]，选择SFO，并从JFK可选列表中删除SFO
4. 当前节点变为SFO，其可前往节点的可选列表为[ATL]，选择ATL，并从SFO可选列表中删除ATL
5. 当前节点变为ATL，其可选列表为[SFO]，选择SFO，并从ATL的可选列表中删除SFO。
6. 当前节点变为SFO，其可选前往点的可选列表为空，结束这条路径。
7. 至此，所有节点的可选列表变为空，说明此时所有的机票都用完。上述当前节点排序就是答案。

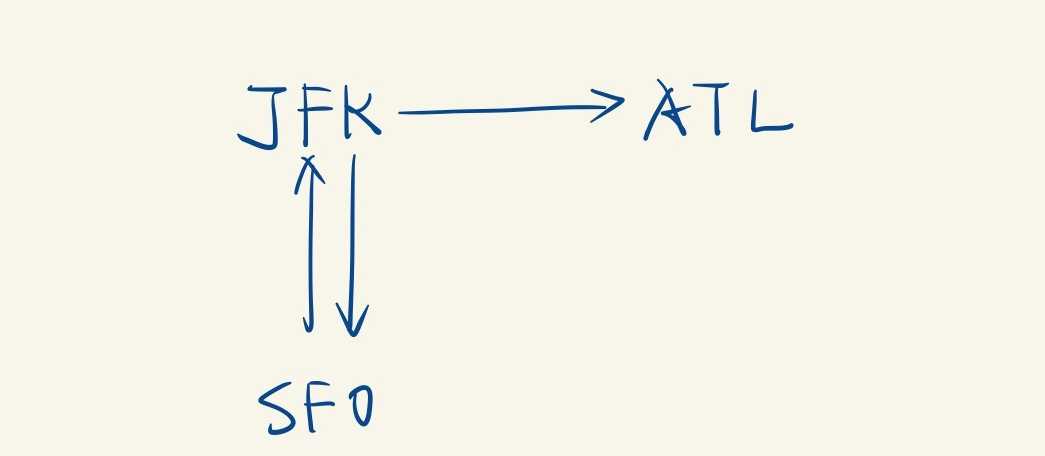
考虑下面这种情况：

1. 当前节点为JFK，可前往节点列表为[SFO, ATL]，根据最小的原则，选择ATL，从SFO的可选列表中删除ATL
2. 当前节点变为ATL，其不是一个出发点， 没有可选列表。
3. 由于路径中还有节点可前往列表不为空，因此显然不是答案。
4. 回溯到节点可选列表不为空的节点JFK，可选列表为[SFO]，选择SFO，并从JFK的可选列表中删除SFO
5. 当前节点为SFO，可选列表为[JFK]，选择回到JFK
6. 由于题目假设一定有这样的路径，所有一定可以从分叉点出发，回到分叉点。

4. 数据结构的选择

1. 为每个出发点，简历一个可选择列表，这个可选列表用PriorityQueue实现，可以在O(lgk)时间得到最大的String。
2. 每个出发点和可前往列表存为一个Map: Map<String, PriorityQueue>
3. 因此考虑到情况二，回溯访问的节点在之前节点的前面，因此采用postOrder遍历。
4. 添加结果到result中，add(0, element)

5. 代码示例

class Solution {
    public List<String> findItinerary(List<List<String>> tickets) {
        // 初始化Map<出发点，对应可抵达队列>
        Map<String, Queue<String>> map = new HashMap<>();
        for (List<String> ticket : tickets) {
            if (!map.containsKey(ticket.get(0))) {
                map.put(ticket.get(0), new PriorityQueue<String>());
            }
            map.get(ticket.get(0)).add(ticket.get(1));
        }
        
        String beginWith = "JFK";
        List<String> result = new ArrayList<>();
        dfs(beginWith, map, result);
        
        // int begin = 0;
        // int end = postorder.size() - 1;
        // while (begin < end) {
        //     String temp = postorder.get(begin);
        //     postorder.set(begin, postorder.get(end));
        //     postorder.set(end, temp);
        //     begin++;
        //     end--;
        // }
        return result;
        
    }
    private void dfs(String beginWith, Map<String, Queue<String>> map, List<String> postorder) {
        // if (!map.containsKey(beginWith) || map.get(beginWith).isEmpty()) {
        //     postorder.add(0, beginWith);
        //     return; 
        // }
        // while(!map.get(beginWith).isEmpty()) {
        //     dfs(map.get(beginWith).poll(), map, postorder);
        // }
        // postorder.add(0, beginWith);
        // 优化后的代码
        if (map.containsKey(beginWith)) { // 如果beginWith是一个出发点，对其进行后续遍历
            while(!map.get(beginWith).isEmpty()) { // 多叉树的后续遍历模版
                dfs(map.get(beginWith).poll(), map, postorder);  // 使用queue的poll()方法，将已经访问过的节点从可选列表中弹出
            }
        }
        // 访问完beginWith的所有children后，加入beginWith
        // 采用了add(index, element)不需要后续在反转结果
        postorder.add(0, beginWith);
    }
}

332. Reconstruct Itinerary

原文：https://www.cnblogs.com/isguoqiang/p/11605920.html