1 为何使用RNN（Recurrent Neural Network）

传统神经网络，如卷积，全连接神经网络，同样的输入只能输出相同的输出。但在如语义识别的时候我们想要相同的输入对应不同的输出。如购票系统中，去‘’北京‘’，中的北京是目的地，而离开’北京‘，’中的北京是出发地。通过上下文来跟当前的输入来决定输出就需要使用RNN。

2 简单RNN

如下图是一个简单的RNN模型，输入层有两个神经元\((x_1,x_2)\)，隐藏层有两个神经元，输出层有两个神经元\((y_1,y_2)\)。若没有记忆单元\((a_1,a_2)\)，相同的输入\((x_1,x_2)\)一定会输出相同的\((y_1,y_2)\)。若加上记忆单元\((a_1,a_2)\)，在计算隐藏层的时候为，记忆单元乘以相应的权重\(+\)输入层乘以相应的权重，得到隐藏层，再把隐藏层的值存入记忆单元\((a_1,a_2)\)中，下次在计算隐藏层的值的时候，\((a_1,a_2)\)的值已经改变，所以算出的隐藏层的值不同，因此输出也不同。这是简单的RNN，至少实现了记忆功能。

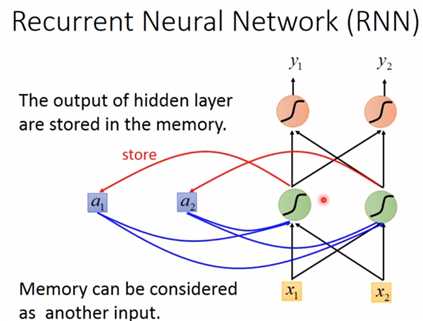
出来上面的结构形式，还有如下图的简单RNN，区别就是一个把隐藏层的值传给记忆单元，一个把输出值传给记忆单元。

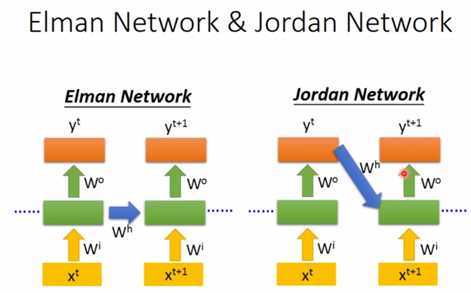
还有双向循环神经网络，通过把正向RNN跟反向RNN的隐藏层结合起来输出，来训练网络

3 LSTM（Long Short-Term Memory）

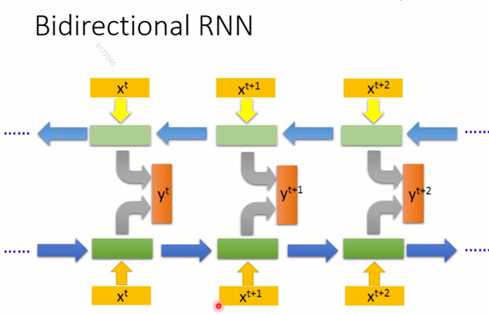
现在LSTM已经成了RNN的标准，与简单RNN不同的是，LSTM的记忆单元，由三个门控制，分别为

1. 输入门（是否隐藏层的值要写入到记忆单元中）
2. 遗忘门（当前记忆单元内的值是否需要洗掉）
3. 输出门（是否输出新的记忆单元的值）

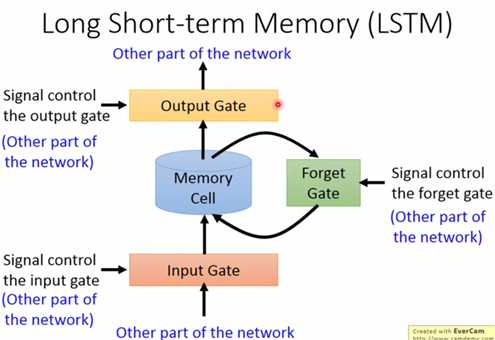
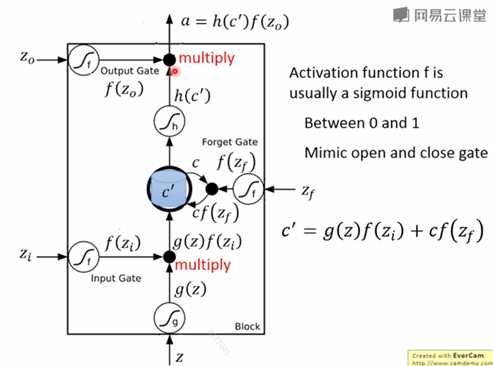
每个门都是一个向量，与对应需要控制的向量做元素之间的乘法，得到一个向量。基本运算如下图，即：

新的记忆单元=输入门×输入+遗忘门×记忆单元

输出向量 = 输出门×新记忆单元?

这里省去了激活函数

这里的三个门的计算都为：

输入门=输入向量x×转换矩阵

遗忘门门=输入向量x×转换矩阵

输入门=输入向量x×转换矩阵

其中x可以被认为对应隐藏层的值，因为是通过隐藏层的值来更新存储单元

最终形式为

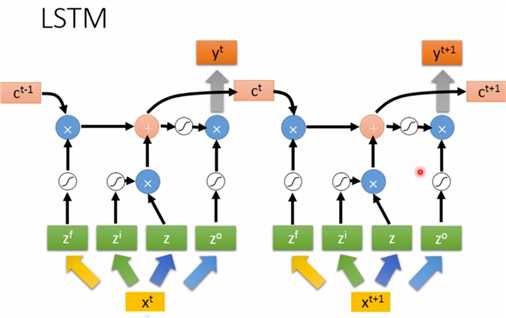
注意，上图的\(x^t,x^{t+1}\)用的是同一个网络，即求\(z^f,z^i,z,z^o\)时的参数矩阵相同

RNN循环神经网络

原文：https://www.cnblogs.com/lolybj/p/11503921.html