凸集的定义:设集合\(D\in R^n\),若对于任意两点\(x,y\in D\),以及实数\(\alpha(0\leq\alpha\leq1)\),都有:
\[ \alpha x+(1-\alpha)y\in D \]
则称集合\(D\)为凸集
仿射集合:如果集合\(C\in R^n\)中任意两个不同点之间直线上的点仍然在集合\(C\)中,那么称集合\(C\)是仿射的。
凸锥:如果对于任意\(x\in C\)和\(\theta\geq 0\)都有\(\theta x\in C\),我们称集合\(C\)是锥或者非负齐次。如果集合\(C\)是凸的,则称\(C\)为凸锥,即对于任意\(x_1, x_2\in C\)和\(\theta_1, \theta_2\geq 0\),都有
\[\theta_1x_1+\theta_2x_2\in C\]
超平面:超平面是具有下面形式的集合
\[\\{x|a^Tx=b\\}\]
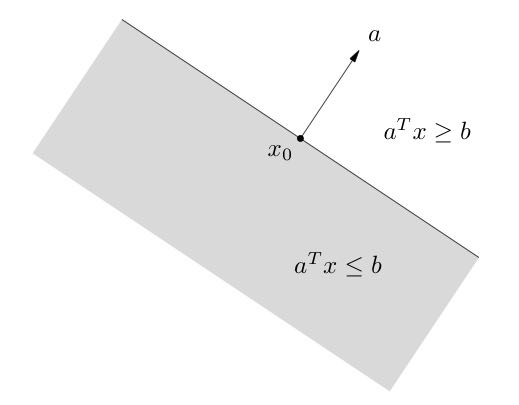
其中\(a\in R^n, a\neq 0\)且\(b\in R\)。这里\(a^Tx_0=b\),进一步地\(a^T(x-x_0)=0\),所以\(a\)是\(x-x_0\)的法向量,超平面如上图所示。解析地,超平面是关于\(x\)的非平凡线性方程的解空间(因此是一个仿射集合)。\(\\{x|a^Tx\leq b\\}\)称为半平面,半平面是凸的,但不是仿射的。
Euclid球和椭球:\(R^n\)空间中的Euclid球(或简称为球)具有下面的形式,
\[B(x_c,r)=\\{x|~\Vert x-x_c\Vert_2\leq rx\\}=\\{x|(x-x_c)^T(x-x_c)\leq r^2\\}\]
其中\(r>0\),\(\Vert \cdot \Vert_2\)表示Euclid范数,也即\(\Vert u\Vert_2=(u^Tu)^{1/2}\),向量\(x_c\)是球心,标量\(r\)为半径。Euclid球的另一个常见的表达式为,\[B(x_c,r)=\\{x_c+ru|~\Vert u\Vert_2\leq 1\\}\]Euclid球是凸集。
椭球具有如下形式,\[\epsilon=\\{x~|~(x-x_c)^TP^{-1}(x-x_c)\leq 1\\}\]
其中\(P=P^T\succ 0\),也即\(P\)是对称正定矩阵,\(x_c\)为椭球的中心。椭球的另外一种表示形式为\(\epsilon=\\{x_c+Au~|~\Vert u\Vert_2\leq 1\\}\),其中\(A\)是非奇异的方阵,且\(A=P^{1/2}\)。
单纯形:设\(k+1\)个点\(v_0, ..., v_k\in \mathbf{R}^n\)仿射独立,即\(v_1-v_0, ..., v_k-v_0\)线性独立,那么这些点决定了一个单纯形如下 \[C={\rm conv}\\{v_0, ..., v_k\\}=\\{\theta_0v_0+\cdots+\theta_kv_k~|~\theta\succeq0,\bf{1}^T\theta=1\\}\]这个单纯形的仿射维数为\(k\),因此也称为\(\mathbf{R}^n\)空间的\(k\)维单纯形。
单纯形是代数拓扑中最基本的概念。单纯形是三角形和四面体的一种泛化,一个k维单纯形是指包含 k+1个节点的凸多面体。
用\(S^n\)表示对称\(n\times n\)矩阵的集合,即
\[S^n=\\{X\in R^{n\times n}~|~X=X^T\\}\]
用\(S^n_+\)表示对称半正定矩阵的集合,即
\[S^n_+=\\{X\in S^n~|~X\succeq 0\\}\]
用\(S^n_{++}\)表示对称正定矩阵的集合,即
\[S^n_{++}=\\{X\in S^n~|~X\succ 0\\}\]
集合\(S^n_+\)是一个凸锥:如果\(\theta_1, \theta_2\geq 0\)并且\(A, B\in S^n_+\),那么\(\theta_1A+\theta_2B\in S^n_+\)
1、交集:任意有限个甚至无限个凸集的交集运算是保凸的。
2、仿射变换:函数\(f : R^n\rightarrow R^m\) 是仿射的,如果它是一个线性函数和一个常数的和,即具有\(f(x)=Ax+b\) 的形式,其中\(A\in R^{m\times n}, b\in R^m\)。特别地,如果\(S\subseteq R^n\)是凸集,\(\alpha\in R\)并且\(\alpha\in R^n\),那么集合\(\alpha S\)(伸缩变换)和\(S+\alpha\)(平移变化)都是凸的。
3、求和运算:多个凸集求和仍然是凸集。
4、透视函数:\(P : R^{n+1}\rightarrow R^n, P(z,t)=z/t\)为透视函数,其定义域为\({\rm dom} P=R^n\times R_{++}\),透视函数对向量进行伸缩或称为规范化,使得最后一维分量为1并舍弃之,也即降维。如果透视函数的定义域\(A\)为凸集,那么经过透视函数作用后 \(P(A)\) 也是凸集(保凸性)。
5、线性分式函数:由透视函数和仿射函数复合而成,设\(g : R^n\rightarrow R^{m+1}\)是仿射的,即
\[g(x)=\begin{bmatrix}A\\\\ c^T\end{bmatrix}x+\begin{bmatrix}b\\\\ d\end{bmatrix}\]
其中\(A\in R^{m\times n}, b\in R^m, c\in R^n\),并且\(d\in R\),给出复合函数\(f=P(g) : R^N\rightarrow R^m\)
\[f(x)=(Ax+b)/(c^Tx+d),~~~{\rm dom}f =\\{c^Tx+d>0\\}\]
可见线性分式函数将维度从\(n\)为降到\(m\)维。线性分式函数具有保凸性。
对偶锥:令\(K\)为一个锥。集合
\[K^\ast=\\{y~|~x^Ty\geq 0, \forall x\in K\\}\]
称为\(K\)的对偶锥。\(K^\ast\)是一个锥,并且它总是凸的(即使\(K\)不是凸锥)。
对偶锥的性质:
广义不等式:正常锥 \(K\) 可以用来定义广义不等式,即 \(R^n\) 上的偏序关系,定义如下,
\[x\succeq K y\Longleftrightarrow y-x\in K\]
当 \(K=R_+\) 时,偏序关系 \(\succeq K\) 就是通常意义上 \(R\) 中的序 \(\geq\)。
凸函数定义:设\(f(x)\)为定义在凸集合\(D\)上的函数,对于\(D\)上任意两点\(x_1,x_2\in D\)和任意实数\(\lambda\in[0,1]\),总有:
\[
f(\lambda x_1+(1-\lambda)x_2)\leq \lambda f(x_1)+(1-\lambda)f(x_2)
\]

凸函数的判断方法:
(1)一阶条件:dom \(f\) 是凸集且对于任意 \(x, y\in\) dom \(f\),满足\(f(y)\geq f(x)+\nabla f(x)^T(y-x)\)(如果是严格凸则去掉“=”)
(2)二阶条件:函数\(f\)是二阶可微,也即它的 Hessian 矩阵或者二阶导数 \(\nabla^2f\) 存在,则函数 \(f\) 是凸函数的充要条件是它的 Hessian 矩阵半正定(也即 \(\nabla^2f(x)\succeq 0\))
Hessian矩阵:若\(n\)元函数\(f(x)\)具有二阶偏导数,也即\(\frac{\partial^2 f(x)}{\partial x_i\partial x_j}\)都存在,则称矩阵
\[ \nabla^2 f(x)= \begin{pmatrix} \frac{\partial^2 f(x)}{\partial x_1\partial x_1} & \frac{\partial^2 f(x)}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2 f(x)}{\partial x_1\partial x_n}\\\\frac{\partial^2 f(x)}{\partial x_2\partial x_1} & \frac{\partial^2 f(x)}{\partial x_2\partial x_2} & \cdots & \frac{\partial^2 f(x)}{\partial x_2\partial x_n}\\\\vdots & \vdots & & \vdots\\\\frac{\partial^2 f(x)}{\partial x_n\partial x_1} & \frac{\partial^2 f(x)}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2 f(x)}{\partial x_n\partial x_n}\\\\end{pmatrix} \]
为\(f(x)\)在\(x\)处的 Hessian 矩阵
常见的凸函数:
补充:一个函数的原函数和反函数的单调性相同,但是凹凸性之间没有联系。
函数 \(f : R^n\rightarrow R\) 的 \(\alpha-\) 下水平集定义为 \[C_{\alpha}=\\{x\in {\rm dom} f~|~f(x)\leq\alpha\\}\]
对于任意 \(\alpha\) 值,凸函数的下水平集仍然是凸集。 例如集合 \(\\{x\in R^n_+~|~G(x)\geq \alpha A(x)\\}\),其中 \(0\leq\alpha\leq 1\), \(G(x)=\Big(\prod_{i=1}^nx_i\Big)^{1/n}\),\(A(x)=\frac{1}{n}\sum_{i=1}^nx_i\),该集合是凸集,因为它是凹函数 \(G(x)-\alpha A(x)\) 的0-上水平集。反过来不一定正确:某个函数的所有下水平集都是凸集,但是这个函数可能不是凸函数 (后面将给出这样的函数定义为"拟凸函数")。
函数 \(f : R^n\rightarrow R\) 的图像定义为 \[\\{(x, f(x))~|~x\in {\rm dom} f\\}\] 它是 \(R^{n+1}\) 空间的一个子集。函数 \(f : R^n\rightarrow R\) 的上镜图定义为 \[{\rm epi} f =\\{(x, t)~|~x\in{\rm dom} f, f(x)\leq t\\}\] 它也是 \(R^{n+1}\) 空间的一个子集。与上镜图相对应的是亚图:\[{\rm hypo} f =\\{(x, t)~|~x\in{\rm dom} f, t\leq f(x)\\}\]
凸集和凸函数的联系可以通过上镜图和亚图来建立:一个函数是凸函数,当且仅当其上镜图是凸集;一个函数是凹函数,当且仅当其亚图是凸集。这些关系可以用下图所示
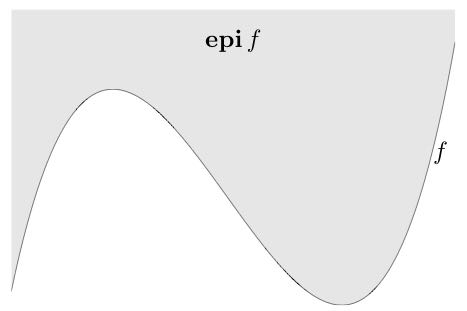
运用上镜图可以判断矩阵分式函数 \(f : R^n\times S^n\rightarrow R\),\[f(x, Y)=x^TY^{-1}x\]在定义域 dom \(f=R^n\times S^n_{++}\) 上是凸的,这是因为 \[{\rm epi} f=\\{(x, Y, t)~|~Y\succ 0, x^TY^{-1}x\leq t\\}=\Big\\{(x, Y, t)~\Big |~\begin{bmatrix}Y & x\\\\ x^T & t\\\\ \end{bmatrix}\succeq 0, Y\succ 0\Big\\}\] 利用 Schur 补条件容易判断分块矩阵 \(\begin{bmatrix}Y & x\\\\ x^T & t\\\\ \end{bmatrix}\)经过行初等变换得到\(\begin{bmatrix}Y & x\\\\ 0 & t-x^TY^{-1}x\\\\ \end{bmatrix}\),所以原矩阵分式函数是凸的等价于上镜图是凸集,并进一步等价于矩阵\(\begin{bmatrix}Y & x\\\\ x^T & t\\\\ \end{bmatrix}\)是半正定且\(Y\)是正定的。
常见函数保凸运算
设函数 \(f : R^n\rightarrow R\),定义函数 \(f^\ast : R^n\rightarrow R\) 为
\[f^\ast(y)=\sup\limits_{x\in {\rm dom} f} (y^Tx-f(x))\]
此函数称为函数 \(f\) 的共轭函数。容易知道无论 \(f(x)\) 是否是凸函数,它的共轭函数 \(f^\ast(y)\) 一定是一个凸函数。
如何求解共轭函数? 假设有函数 \(f(x) = x^TQx/2\),其中 \(Q\) 是可逆的对称阵,根据定义有:\(f^\ast(y)=\sup\\{y^Tx- x^TQx/2\\}\),现在用 \(f^\ast(y)\) 对 \(x\) 求导并令其为0得到 \(y-Qx=0\),所以 \(x=Q^{-1}y\) ,代入得共轭函数为 \(f^\ast(y)= y^TQ^{-1}y/2\).
Fenchel 不等式:根据共轭函数的定义可以得到,对任意 \(x\) 和 \(y\),如下不等式成立:
\[f(x)+f^\ast(y)\geq x^Ty\]
上述不等式称为 Fenchel 不等式 (当 \(f\) 可微时也称为 Young 不等式)。
上面例子中 \(f(x) = x^TQx/2\) 的共轭函数为 \(f^\ast(y)= y^TQ^{-1}y/2\),利用 Fenchel 不等式可以得到:\(f(x)+f^\ast(y)=x^TQx/2+y^TQ^{-1}y/2\geq x^Ty\)
共轭函数的性质:
函数 \(f : R^n\rightarrow R\) 称为拟凸函数 (或者单峰函数),如果其定义域及所有下水平集
\[S_\alpha=\\{x\in{\rm dom} f~|~f(x)\leq\alpha\\}, \alpha\in R\]
都是凸集。函数 \(f\) 是拟凹函数,如果 \(-f\) 是拟凸函数,即每个上水平集 \(\\{x~|~f(x)\geq\alpha\\}\) 是凸集。若某函数既是拟凸函数又是拟凹函数,其为拟线性函数。函数是拟线性函数,如果其定义域和所有的水平集 \(\\{x~|~f(x)=\alpha\\}\) 都是凸集。如下图所示单峰函数,函数 \(f(x)\) 是关于 \(\alpha\) 和 \(\beta\) 的拟凸函数。
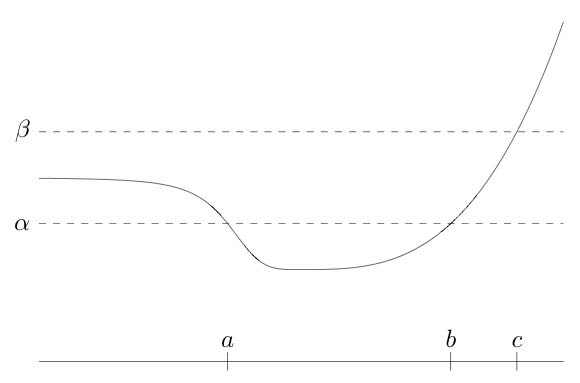
根据拟凸函数的定义,函数值小于某个常数的定义域区间构成凸集,显然对于多峰函数,存在多段不相连的定义域区间内函数值满足小于某个常数值,而这些区间因为不连通自然不是凸集,所以多峰函数不是拟凸函数。
因为 \(R\) 上的单峰函数在任意的有界闭区间内同样也是单峰函数,此外单峰函数的最大值点一定在边界处取得,所以我们容易得到:函数 \(f\) 是拟凸函数的充要条件是,\({\rm dom} f\) 是凸集,且对于任意 \(x, y\in {\rm dom} f\) 及 \(0\leq\theta\leq 1\) 有
\[f(\theta x+(1-\theta)y)\leq\max\\{f(x), f(y)\\}\]
即线段中任意一点的函数值不超过其端点函数值中最大的那个。
\(R\) 上的拟凸函数:连续函数 \(f : R\rightarrow R\) 是拟凸的,当且仅当下述条件至少有一个成立,
以上三个条件本质上是对单峰函数的三种可能情况的描述。
可微的拟凸函数:
一阶条件:设函数 \(f : R^n\rightarrow R\) 可微,则函数 \(f\) 是拟凸的充要条件是,\({\rm dom} f\) 是凸集,且对于任意 \(x, y\in {\rm dom} f\) 有
\[f(y)\leq f(x)\Longrightarrow\nabla f(x)^T(y-x)\leq 0\]
凸函数和拟凸函数都是单峰函数,但是凸函数还要求这个单峰函数上点的斜率是单调递增的,而拟凸函数则不需要此条件,这就导致了凸函数导数为0的点最多只有一个且一定是全局最小点,而拟凸函数导数为0的点可能有多个且不是全局最小点。
二阶条件:假设函数 \(f\) 二次可微。如果函数 \(f\) 是拟凸函数,则对于任意 \(x\in {\rm dom} f\) 以及任意 \(y\in R^n\) 有
\[y^T\nabla f(x)=0\Longrightarrow y^T\nabla^2f(x)y\geq 0\]
对于定义在 \(R\) 上的拟凸函数,上述条件可以简化为如下条件,
\[f'(x)=0\Longrightarrow f''(x)\geq 0\]
即在斜率为零的点,二阶导数是非负的。
一些常见的保拟凸运算有:
称函数 \(f : R^n\rightarrow R\) 对数凹或对数-凹,如果对所有的 \(x\in{\rm dom} f\) 有 \(f(x)>0\) 且 \(\log f\) 是凹函数。称函数对数凸或者对数-凸,如果 \(\log f\) 是凸函数。
对数-凹函数的性质:函数 \(f : R^n\rightarrow R\),其定义域是凸集,且对于任意 \(x\in {\rm dom} f\) 有 \(f(x)>0\),函数是对数-凹的,当且仅当对任意 \(x,y\in {\rm dom} f\),\(0\leq\theta\leq 1\) 有
\[f(\theta x+(1-\theta)y)\geq f(x)^{\theta}f(y)^{1-\theta}\]
特别地,取 \(\theta=1/2\) 有:对数-凹函数在两点之间中点的函数值不小于这两点的函数值的几何平均值。
一些常见对数-凹函数和对数-凸函数
二次可微的对数-凸函数/凹函数
函数 \(f\) 二次可微,则它是对数-凸函数的充要条件是 \(f(x)\nabla^2f(x)\succeq\nabla f(x)\nabla f(x)^T\),\(f\) 是对数-凹函数的充要条件是 \(f(x)\nabla^2f(x)\preceq\nabla f(x)\nabla f(x)^T\)。
对数-凹函数和对数-凸函数的性质
广义不等式的单调性:设 \(K\subseteq R^n\) 是一个正常锥,其相应的广义不等式为 \(\succeq K\),函数 \(f : R^n\rightarrow R\) 称为 \(K\)-非减,如果下式成立
\[x\succeq K~y, \Longrightarrow f(x)\leq f(y)\]
称为 \(K\)-增,如果下式成立
\[x\succeq K~y, x\neq y, \Longrightarrow f(x) < f(y)\]
例如,单调向量函数 \(f(x)\):对于任意的 \(x, y\),满足 \(x_1 \leq y_1, \cdots, x_n \leq y_n \Longrightarrow f(x) \leq f(y)\)。
一阶条件:对于可微函数 \(f\),其定义域为凸集,它是 \(K\)-非减的,当且仅当对于任意的 \(x\in {\rm dom} f\) 有
\[\nabla f(x) \succeq K\ast 0\]
广义不等式的凸性:设 \(K\subseteq R^m\) 是一正常锥,相应的广义不等式为 \(\succeq K\) 。函数 \(f : R^n\rightarrow R^m\) 是 \(K\)-凸的,如果对于任意 \(x, y\),以及 \(0\leq \theta \leq 1\) 有
\[f(\theta x+(1-\theta)y) \succeq K~\theta f(x) + (1-\theta) f(y)\]
函数被称为严格 \(K\)-凸的,如果对任意 \(x\neq y\) 和 \(0<\theta<1\) 有
\[f(\theta x+(1-\theta)y)\succ K~\theta f(x)+(1-\theta)f(y)\]
函数复合保留凸性的很多结论都可以推广到 \(K\)-凸的情形。
凸规划的标准形式:设\(f(x)\)及\(g_i(x),i=1,\dots,m\)均为\(R^n\)上的凸函数,满足以下条件的规划问题称为凸规划:
\[ \begin{split} &\min{f(x)}\\\&s.t.\begin{cases} g_i(x)\leq0,i=1,\dots,m\\\a^T_jx=b_j,j=1,\dots,p \end{cases} \end{split} \]
或者\(f(x)\)为凹函数,\(g_i(x),i=1,\dots,m\)为\(R^n\)上的凸函数:
\[ \begin{split} &\max{f(x)}\\\&s.t.\begin{cases} g_i(x)\leq0,i=1,\dots,m\\\a^T_jx=b_j,j=1,\dots,p \end{cases} \end{split} \]
凸优化问题有三个附加的要求:
一个规划问题如果不能等价于以上两种形式的规划问题,那么这个规划问题是非凸规划问题。
常用等价变换的方法:
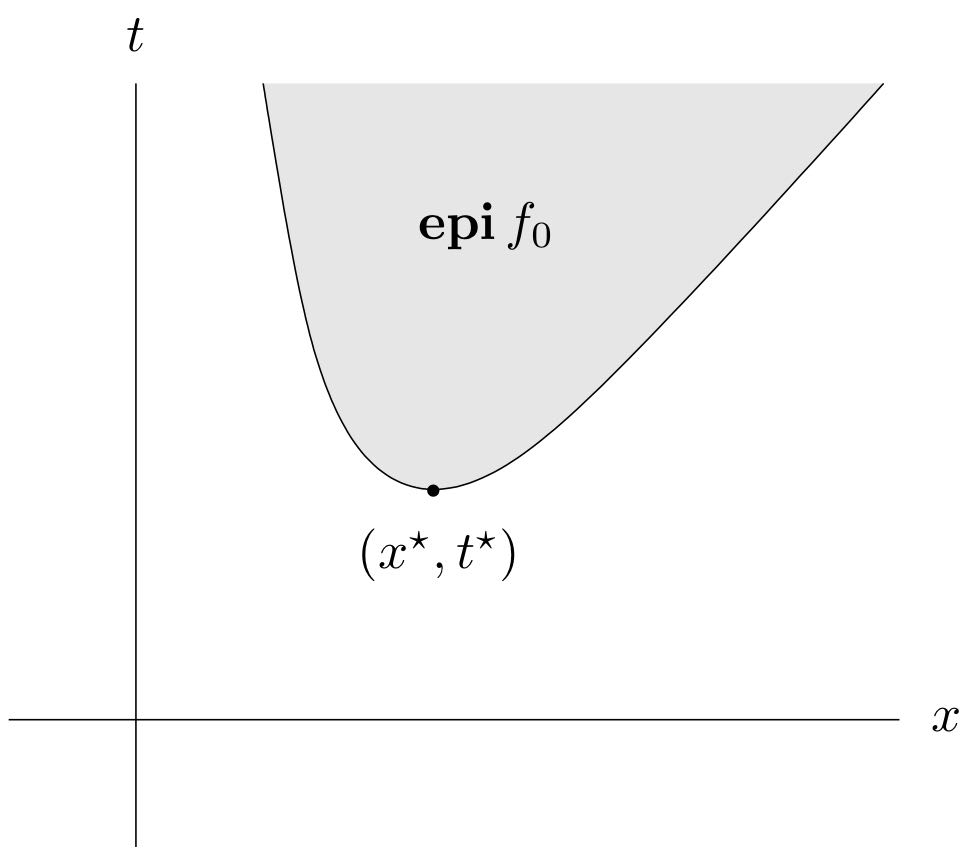
凸优化问题的一个基础性质是其任意局部最优解也是(全局)最优解。对于拟凸优化问题,局部最优解不一定是全局最优解。
可微函数 \(f_0\) 的最优性准则:设凸优化问题的目标函数 \(f_0\) 是可微的,对于所有的 \(x,y\in {\rm dom~}f_0\) 有
\[f_0(y)\geq f_0(x)+\nabla f_0(x)^T(y-x)\]
令 \(X\) 表示其可行集,\(x\) 是最优解,当且仅当 \(x\in X\) 且
\[\nabla f_0(x)^T(y-x)\geq 0, \forall y\in X\]
如果可行域为 \(R\),显然最优解的条件为 \(\nabla f_0(x)=0\),对于可行域有界情况,此时最优解满足条件 (最优解的充要条件) \(\nabla f_0(x)^T(y-x)\geq 0\)
只含等式约束的问题:考虑优化问题:
\[
\min{f(x)}~~~~
s.t.~
a^T_jx=b_j,j=1,\dots,p
\]
利用最优解的条件 \(f_0(x)^T(y-x)\geq 0\) 可以得到以上等式约束的优化问题最优解的条件:\(\nabla f_0(x)+A^Tv=0\),其中 \(v\in R^p\) 且 \(v\in \mathcal{N}(A)\) (\(\mathcal{N}(A)\) 表示算子 \(A\) 的零空间),这是经典的 Lagrange 乘子最优性条件。(推导过程见 P135)
只含不等式约束的问题:考虑优化问题:
\[
\min{f(x)}~~~~
s.t.~
x\succeq 0
\]
利用最优解的条件 \(f_0(x)^T(y-x)\geq 0\) 可以得到以上不等式约束的优化问题最优解的条件:\(x\succeq 0, \nabla f_0(x)\succeq 0, x_i(\nabla f_0(x))_i=0, i=1, \dots, n\)。
拟凸优化问题:可以通过一族凸不等式来表示拟凸函数的下水平集,这是解决拟凸优化问题的一般方法。令 \(\phi_t : R^n\rightarrow R, t\in R\) 为满足
\[f_0(x)\leq t\Longleftrightarrow \phi_t(x)\leq 0\]
线性规划问题的一般形式:
\[
\begin{split}
&{\rm minimize}~~c^Tx+d\\\&s.t.
\begin{cases}
Gx\preceq h \\\Ax=b.
\end{cases}
\end{split}
\]
分片线性极小化:
考虑极小化(无约束)分片线性凸函数的问题:
\[
f(x)=\max\limits_{i=1,\dots,m} (a_i^Tx+b_i)
\]
该问题可以利用上镜图化为线性规划
\[
\begin{split}
&{\rm minimize}~~t\\\&s.t.
\max\limits_{i=1,\dots,m} (a_i^Tx+b_i)\leq t
\end{split}
\]
进一步地,
\[
\begin{split}
&{\rm minimize}~~t\\\&s.t.~a_i^Tx+b_i\leq t, i=1,\dots,m.
\end{split}\]
线性分式规划问题:
\[
\begin{split}
&{\rm minimize}~~f_0(x)\\\&s.t.
\begin{cases}
Gx\preceq h\\\Ax=b
\end{cases}
\end{split}
\]
其中目标函数为
\[f_0(x)=\frac{c^Tx+d}{e^Tx+f}, {\rm dom~} f_0=\\{x|e^Tx+f>0\\}\]
如何将以上非凸规划问题转化为线性规划问题呢?
通过观察我们发现目标函数是由线性函数经过变换得到的,不妨引入新变量将目标函数转化为线性函数,令
\[y=\frac{x}{e^Tx+f}, z=\frac{1}{e^Tx+f}\]
其中,\(x=y/z\)。将以上变换带入原优化问题中可以得到如下等价的线性优化问题
\[
\begin{split}
&{\rm minimize}~~c^Ty+dz\\\&s.t.
\begin{cases}
Gy-hz\preceq 0\\\Ay-bz=0\\\e^Ty+fz=1\\\z\geq 0
\end{cases}
\end{split}
\]
其中 \(y, z\) 为优化变量。
广义线性分式规划
线性分式规划的一个推广是广义线性分式规划,其中
\[f_0(x)=\max\limits_{i=1,\dots,r} \frac{c_i^Tx+d_i}{e_i^Tx+f_i},~~{\rm dom~} f_0=\\{x|e_i^Tx+f_i>0, i=1,\dots,r\\}\]
该问题是分片线性极小化问题和线性分式规划问题的组合形式,可以转化为相应的线性规划问题。
二次优化问题:
当凸优化问题的目标函数是凸二次型并且约束函数为仿射时,该问题称为二次规划(QP),二次规划可以表述为
\[
\begin{split}
&{\rm minimize}~ (1/2)x^TPx+q^Tx+r\\\&s.t.~\begin{cases}
Gx\preceq h\\\Ax=b
\end{cases}
\end{split}
\]
其中 \(P\in S_+^n, G\in R^{m\times n}\) 并且 \(A\in R^{p\times n}\)
例如,最小二乘以及回归都是二次规划问题。
二阶锥规划:
一个与二次规划紧密相关的问题是二阶锥规划(SOCP):
\[
\begin{split}
&{\rm minimize}~ f^Tx\\\&s.t.~\begin{cases}
\Vert A_ix+b_i\Vert_2\leq c_i^Tx+d_i, \quad i=1,\dots,m\\\Fx=g
\end{cases}
\end{split}
\]
其中,\(x\in R^n\) 为优化变量,\(A_i\in R^{n_i\times n}\) 且 \(F\in R^{p\times n}\)。二阶锥规划问题是很多优化问题的一般形式(如鲁棒线性规划,随机约束线性规划,极小曲面问题)。
几何规划自然的形式不是凸的,但是可以通过一些变换将其转化为凸优化问题。
单项式与正项式的定义:函数 \(f : R^n\rightarrow R, {\rm dom}~f=R^n_{++}\) 定义为
\[
f(x)=cx_1^{a_1}x_2^{a_2}\cdots x_n^{a_n},
\]
其中 \(c>0, a_i\in R\)。它被称为单项式函数或者简称单项式。单项式的和被称为正项式函数或者简称正项式,它具有以下形式
\[
f(x)=\sum_{k=1}^Kc_kx_1^{a_{1k}}x_2^{a_{2k}}\cdots x_n^{a_{nk}},
\]
其中 \(c_k>0\)。
几何规划:具有下列形式的优化问题
\[
\begin{split}
&{\rm minimize}~~f_0(x)\\\&s.t.~
\begin{cases}
f_i(x)\leq 1, \quad i=1,\cdots,m\\\h_i(x)=1, \quad i=1,\cdots,p.
\end{cases}
\end{split}
\]
被称为几何规划(GP),其中 \(f_0,\dots,f_m\) 为正项式,\(h_1,\cdots, h_p\) 为单项式,定义域为 \(\mathcal{D}=R_{++}^n\)
一个优化问题如果具有以下一些特征:
那么就有可能转化为几何规划。
几何规划一般不是凸优化问题,但是可以通过转换将几何规划问题转化为凸优化问题。
对于包含 \(x\) 的单项式函数,即
\[f(x)=cx_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}\]
利用变换 \(y_i=\log x_i\) 有 \(x_i=e^{y_i}\),将此式带入到 \(f(x)\) 中得
\[
\begin{split}
f(x)
&=f(e^{y_1},\cdots,e^{y_n})\\\&=c(e^{y_1})^{a_1}\cdots(e^{y_n})^{a_n}\\\&=e^{a^Ty+b}
\end{split}
\]
其中 \(b=\log c\)。
类似地,可以将以下正项式
\[
f(x)=\sum_{k=1}^Kc_kx_1^{a_{1k}}x_2^{a_{2k}}\cdots x_n^{a_{nk}},
\]
转化为
\[
f(x)=\sum_{k=1}^Ke^{a_k^Ty+b_k}
\]
所以原始的几何规划问题可以转化为以下问题
\[
\begin{split}
&{\rm minimize}~~\sum_{k=1}^{K_0}e^{a_{0k}^Ty+b_{0k}}\\\&s.t.~
\begin{cases}
\sum_{k=1}^{K_i}e^{a_{ik}^Ty+b_{ik}}\leq 1,\quad i=1,\cdots, m\\\e^{g_i^T+h_i}=1, \quad i=1,\cdots, p.
\end{cases}
\end{split}
\]
对比一下以上问题和凸优化问题的差别,虽然以上问题的目标函数和不等式约束都是凸函数,但是凸优化还要求不等式约束的右端项为0以及等式部分是仿射的,为了将以上问题化为等价的凸优化形式,不妨对以上优化问题的目标函数和约束函数取对数进行转换(由于目标函数是单调递增的凸函数,目标函数部分其实可以不用取对数),从而得到如下凸形式的优化问题
\[
\begin{split}
&{\rm minimize}~~\log\left (\sum_{k=1}^{K_0}e^{a_{0k}^Ty+b_{0k}}\right )\\\&s.t.~
\begin{cases}
\log\left (\sum_{k=1}^{K_i}e^{a_{ik}^Ty+b_{ik}}\right )\leq 0,\quad i=1,\cdots, m\\\g_i^T+h_i=0, \quad i=1,\cdots, p.
\end{cases}
\end{split}
\]
以上凸优化问题的解 \(y\) 即是几何规划问题的解,再利用 \(x_i=e^{y_i}\) 即可求出原问题的解 \(x\)。
常见几何规划问题:
Perron-Frobenius 定理指出 \(\lambda\) 满足
\[\lambda=\inf\\{\lambda~|~Av\preceq\lambda v, v\succ 0\\}\]
其中不等式 \(Av\preceq\lambda v\) 可以表示为
\[\sum_{j=1}^nA_{ij}v_j/(\lambda v_i)\leq 1, \quad i=1,\cdots,n\]
矩阵特征值优化问题:
矩阵 \(A(x)\) 的元素为某些基本变量 \(x\) 的正项式函数,如何选择 \(x\) 才能使得 \(A(x)\) 的谱半径最小?针对该问题,我们可以写成以下形式
\[
\begin{split}
&{\rm minimize}~~\lambda(A(x))\\\&s.t. \begin{cases}
\sum_{j=1}^nA_{ij}v_j/(\lambda v_i)\leq 1, \quad i=1,\cdots, n,\\\f_i(x)\leq 1, \quad i=1,\cdots, p.
\end{cases}
\end{split}
\]
其中第一个约束条件为 Perron-Frobenius 定理导出的条件,第二个关于 \(f_i(x)\) 的约束条件由实际问题给出,且 \(f_i(x)\) 是正项式。以上优化问题的优化变量是 \(x, v, \lambda\)。显然该问题为几何规划问题,可以化为凸优化问题。
考虑标准形式的优化问题
\[
\begin{split}
&{\rm minimize}~~f_0(x)\\\&s.t.
\begin{cases}
f_i(x)\leq 0, \quad i=1,\dots, m\\\h_i(x)=0, \quad i=1,\dots, p.
\end{cases}
\end{split}\tag{BP}
\]
定义该问题的 Lagrange 函数 \(L : R^n\times R^m\times R^p\rightarrow R\) 为
\[
L(x,\lambda,v)=f_0(x)+\sum_{i=1}^m\lambda_if_i(x)+\sum_{i=1}^pv_ih_i(x)
\]
其中定义域为 \({\rm dom}~L=\mathcal{D}\times R^m\times R^p\)。\(\lambda_i\) 称为第 \(i\) 个不等式约束 \(f_i(x)\leq 0\) 对应的 Lagrange 乘子,\(v_i\) 称为第 \(i\) 个不等式约束 \(h_i(x)=0\) 对应的 Lagrange 乘子。\(\lambda\) 和 \(v\) 称为对偶变量或者 Lagrange 乘子向量。
Lagrange 对偶函数 \(g : R^m\times R^p\rightarrow R\) 为 Lagrange 函数关于 \(x\) 取得最小值:即对 \(\lambda\in R^m, v\in R^p\),有
\[
g(\lambda, v)=\inf\limits_{x\in\mathcal{D}}L(x,\lambda,v)=\inf\limits_{x\in\mathcal{D}}\left (f_0(x)+\sum_{i=1}^m\lambda_if_i(x)+\sum_{i=1}^pv_ih_i(x)\right )
\]
如果 Lagrange 函数关于 \(x\) 无下界,则对偶函数取值为 \(-\infty\)。
最优值的下界:对偶函数构成了(BP)问题最优值 \(p^\ast={\rm minimize}~f_0(x)\) 的下界,即对任意 \(\lambda\succeq 0\) 和 \(v\) 下式成立
\[g(\lambda,v)\leq p^\ast\]
虽然以上不等式给出来原优化问题的下界,但是当 \(g(\lambda,v)=-\infty\) 时其意义不大。只有当 \(g(\lambda,v)>-\infty\) 时,对偶函数才能给出 \(p^\ast\) 的一个非平凡下界。称满足 \(\lambda\succeq 0\) 以及 \((\lambda,v)\in {\rm dom}~g\) 的 \((\lambda, v)\) 是对偶可行的。
Lagrange 对偶函数和共轭函数
共轭函数:函数 \(f : R^n\rightarrow R\) 的共轭函数 \(f^\ast\) 为
\[f^\ast(y)=\sup\limits_{x\in {\rm dom}~f}(y^Tx-f(x))\]
考虑如下优化问题,其具有线性不等式以及等式约束,
\[
\begin{split}
&{\rm minimize}~~f_0(x)\\\&s.t.
\begin{cases}
Ax\preceq 0\\\Cx=d.
\end{cases}
\end{split}
\]
则以上优化问题的对偶函数表述为
\[
\begin{split}
g(\lambda, v)&=\inf\limits_x~(f_0(x)+\lambda^T(Ax-b)+v^T(Cx-d))\\\&=-b^T\lambda-d^Tv+\inf\limits_x~(f_0(x)+(A^T\lambda+C^Tv)^Tx)\\\&=-b^T\lambda-d^Tv-f_0^\ast(-A^T\lambda-C^Tv)
\end{split}
\]
对于任意一组 \((\lambda, v)\),其中 \(\lambda\succeq 0\),Lagrange 对偶函数给出了优化问题 (BP) 的最优值 \(p^\ast\) 的一个下界。因此,我们可以得到和参数 \(\lambda, v\) 相关的一个下界,其中 Lagrange 函数得到的最好的下界表述为以下优化问题
\[
\begin{split}
&{\rm maximize}~~g(\lambda, v)\\\&s.t.~\lambda\succeq 0.
\end{split}\tag{DP}
\]
问题 (BP) 称为原问题,问题 (DP) 称为原问题的对偶问题。满足 \(\lambda\succeq 0\) 和 \(g(\lambda, v)>-\infty\) 的一组解 \((\lambda, v)\) 称为对偶问题 (DP) 的可行解,其中称 \((\lambda^\ast, v^\ast)\) 是对偶最优解或者最优 Lagrange 乘子,如果它是对偶问题 (DP) 的最优解。
对偶约束:
对偶问题要求对偶函数的上界,显然对偶函数取 \(-\infty\) 的情况是不可取的,因此对偶问题中对偶函数的定义域为
\[{\rm dom}~g=\\{(\lambda, v)~|~g(\lambda, v)>-\infty\\}\]
由于对偶函数 \(g\) 是关于 \(\lambda\) 和 \(v\) 的仿射函数,当 \(\lambda\) 和 \(v\) 满足一定的约束条件时对偶函数存在一个下界,这个约束条件就是对偶约束。例如考虑以下的标准线性规划问题
\[
\begin{split}
&{\rm minimize}~~c^Tx\\\&s.t.
\begin{cases}
Ax=b,\\\x\succeq 0.
\end{cases}
\end{split}
\]
的对偶函数为
\[
g(\lambda, v)=\inf\limits_x~L(x, \lambda, v)=-b^Tv+\inf\limits_x~(c+A^Tv-\lambda)^Tx
\]
可以得到
\[
g(\lambda, v)=
\begin{cases}
-b^Tv \quad c+A^Tv-\lambda=0\\\-\infty \quad \text{其他情况}.
\end{cases}
\]
因为对偶问题要求对偶函数取最大值,而 \(-b^Tv>-\infty\),所以可以排除 \(g(\lambda, v)=-\infty\) 的情况,当 \(g(\lambda, v)=-b^Tv\) 时,约束条件 \(c+A^Tv-\lambda=0\) 就是对偶约束。利用对偶约束,原标准线性规划问题的对偶问题可以表述为
\[ \begin{split} &{\rm minimize}~~-b^Tv\\\&s.t. \begin{cases} A^Tv-\lambda+c=0,\\\\lambda\succeq 0. \end{cases} \end{split} \]
也即
\[ \begin{split} &{\rm minimize}~~-b^Tv\\\&s.t.~ A^Tv+c\succeq 0. \end{split} \]
Lagrange 对偶问题的最优值,我们用 \(d^\ast\) 表示,原问题最优值用 \(p^\ast\) 表示,特别地我们有以下非常重要的不等式
\[d^\ast\leq p^\ast\]
即使原问题不是凸问题,上述不等式仍然成立,这个性质称为弱对偶性。定义差值 \(p^\ast-d^\ast\) 是原问题的最优对偶间隙,它给出了原问题最优值以及通过 Lagrange 对偶函数所能得到的最好(最大)下界之间的差值,最优对偶间隙总是非负的。
对偶问题总是凸问题,当原问题很难求解时,弱对偶性给出了原问题最优值的一个下界。
如果等式
\[d^\ast=p^\ast\]
成立,即最优对偶间隙为零,那么强对偶性成立。这说明从 Lagrange 对偶函数得到的最好下界是紧的。
对于一般情况,强对偶性不成立。但是如果原问题是凸问题,强对偶性通常(但不总是)成立,很多研究给出了强对偶性成立的条件(除了凸性条件以外),这些条件称为约束准则。
对于满足凸优化条件的(BP)问题,Slater条件描述如下。
Slater条件:存在一点 \(x\in\mathbf{relint}~\mathcal{D}\) 使得下式成立
\[f_i(x)<0, \quad i=1,\cdots,m, \quad Ax=b\]
满足上述条件的点称为严格可行,此时强对偶性成立。
注:\(\mathbf{relint}~\mathcal{D}\) 表示区域 \(\mathcal{D}\) 的内部。
Slater定理说明,如果凸优化问题的可行域 \(\mathcal{D}\) 内部(不包括边界)存在一点 \(x\) 满足 \(f_i(x)<0, \quad i=1,\cdots,m, \quad Ax=b\),那么强对偶性成立。特别地,当凸优化问题中不等式约束有些是仿射时,例如约束 \(f_1,\dots, f_k\) 是仿射的,则Slater条件可以进一步改进为:存在一点 \(x\in\mathbf{relint}~\mathcal{D}\) 使得
\[f_i(x)\leq 0, \quad i=1,\cdots,k, \quad f_i(x)<0, \quad i=k+1,\cdots,m, \quad Ax=b\]
换言之,仿射不等式部分不需要严格取“小于”符号。
线性规划问题强对偶性都成立。
由前面内容我们知道原问题最优目标函数值 \(p^\ast\) 和对偶问题最优目标函数值 \(d^\ast\) 满足:\(d^\ast\leq p^\ast\)。定义原问题和对偶问题目标函数的差值
\[
f_0(x)-g(\lambda, v)
\]
为原问题可行解 \(x\) 和对偶可行解 \((\lambda, v)\) 之间的对偶间隙,其中原问题和对偶问题的最优解满足:
\[
p^\ast\in [g(\lambda, v), f_0(x)], \quad d^\ast\in [g(\lambda, v), f_0(x)]
\]
区间长度即为定义的对偶间隙。
如果对偶间隙为0时,此时 \(x\) 是原问题的最优解,\((\lambda, v)\) 是对偶问题的最优解。利用这一特点,可以在优化算法中给出非启发式停止准则。原问题给定初值 \(x^0\),对偶问题初值为 \((\lambda^0, v^0)\),第 \(k\) 步迭代的可行解为 \(x^k\) 和 \((\lambda^k, v^k)\),如果给定要求的绝对精读 \(\epsilon_{\rm abs}>0\),那么停止迭代,这种方法可以保证算法终止时,\(x^k\) 是 \(\epsilon_{\rm abs}\)-次优。除了利用差值来定义精度外,也可以利用 \(\frac{f_0(x^k)-g(\lambda^k, v^k)}{g(\lambda^k, v^k)}\leq\epsilon\) 来定义算法终止条件。
假设 \(x^\ast\) 和 \((\lambda^\ast, v^\ast)\) 分别是原问题和对偶问题的最优解,那么一定满足以下关系
\[ \begin{split} f_0(x^\ast) &=g(\lambda^\ast, v^\ast)\\\&=\inf\limits_{x\in\mathcal{D}}L(x,\lambda^\ast,v^\ast)=\inf\limits_{x\in\mathcal{D}}\left (f_0(x)+\sum_{i=1}^m\lambda^\ast_if_i(x)+\sum_{i=1}^pv^\ast_ih_i(x)\right )\\\&\leq f_0(x^\ast)+\sum_{i=1}^m\lambda^\ast_if_i(x^\ast)+\sum_{i=1}^pv^\ast_ih_i(x^\ast)\\\&\leq f_0(x^\ast) \end{split} \]
第一行等式说明最优对偶间隙为零,第二行等式是对偶函数的定义,第三行等式显然成立,最后一行等式成立是因为 \(\lambda^\ast_i\geq 0, f_i(x^\ast)\leq 0, i=1,\dots, m\) 以及 \(h_i(x^\ast)=0, i=1,\dots, p\)。因此,当原问题和对偶问题的最优值都可以达到且相等(强对偶性成立),此时以上不等式左边和右边项相等,可以得到以下结论:最优解可达且强对偶性成立时,满足
\[\sum_{i=1}^m\lambda^\ast_if_i(x)=0\]
由于 \(\lambda^\ast_if_i(x^\ast)\) 每一项都是非正数,所以可以得到
\[\lambda^\ast_if_i(x^\ast)=0,\quad i=1,\dots, m\]
以上等式条件称为互补松弛条件。
假设函数 \(f_0, \cdots, f_m, h_1, \cdots, h_p\) 可微 (不一定是凸函数)。
非凸问题的 KKT 条件:
令 \(x^\ast\) 和 \((\lambda^\ast, v^\ast)\) 分别是原问题和对偶问题的某对最优解,对偶间隙为零。因为 \(L(x, \lambda^\ast, v^\ast)\) 关于 \(x\) 求极小在 \(x^\ast\) 处取得最小值,因此函数在 \(x^\ast\) 处的导数必须为零,即,
\[ \nabla L(x^\ast, \lambda^\ast, v^\ast)=0 \]
因此我们有
\[ \begin{cases} f_i(x^\ast)\leq 0,\quad i=1, \cdots, m\\\h_i(x^\ast)\leq 0,\quad i=1, \cdots, p\\\\lambda^\ast_i\geq 0, \quad i=1, \cdots, m\\\\lambda^\ast_if_i(x^\ast)= 0, \quad i=1, \cdots, m~~\text{(互补松弛条件)}\\\\nabla L(x^\ast, \lambda^\ast, v^\ast)=0 \end{cases}\tag{KKT} \]
其中
\[ \nabla L(x^\ast, \lambda^\ast, v^\ast)=\nabla f_0(x^\ast)+\sum_{i=1}^m\lambda_i^\ast\nabla f_i(x^\ast)+\sum_{i=1}^pv_i^\ast\nabla h_i(x^\ast)=0 \]
以上条件称为 Karush-Kuhn-Tucker (KKT) 条件
对于目标函数和约束函数可微的任意优化问题,如果强对偶性成立,那么任何一对原问题最优解和对偶问题最优解必须满足 KKT 条件,也即满足 KKT 条件是解是原问题和对偶问题最优解的必要条件。
凸问题的 KKT 条件:
当原问题是凸问题时,满足 KKT 条件的解也是原问题和对偶问题的最优解,且对偶间隙为零。
对于凸优化问题,设 \(x^\ast, \lambda^\ast, v^\ast\) 是任意满足 KKT 条件的点,也即
\[ \begin{cases} f_i(x^\ast)\leq 0,\quad i=1, \cdots, m\\\h_i(x^\ast)\leq 0,\quad i=1, \cdots, p\\\\lambda^\ast_i\geq 0, \quad i=1, \cdots, m\\\\lambda^\ast_if_i(x^\ast)= 0, \quad i=1, \cdots, m\\\\nabla L(x^\ast, \lambda^\ast, v^\ast)=0 \end{cases}\tag{KKT} \]
则 \(x^\ast, \lambda^\ast, v^\ast\) 是原问题和对偶问题的最优解。
无论对于凸优化问题还是非凸优化问题,满足 KKT 条件表明原问题和对偶问题的对偶间隙为零,也即强对偶性成立。
若某个凸优化问题具有可微的目标函数和约束函数,且满足 Slater 条件 (即强对偶性成立),那么 KKT 条件是最优性的充要条件。
KKT 条件在优化领域非常重要,在一些特殊的情形下,是可以解析求解 KKT 条件的 (也因此可以求解优化问题)。
例题:注水问题。考虑以下凸优化问题
\[
\begin{split}
&{\rm minimize}~~-\sum_{i=1}
^n\log(\alpha_i+x_i)\\\&s.t.
\begin{cases}
x\succeq 0\\\\mathbf{1}^Tx=1
\end{cases}
\end{split}
\]
其中 \(\alpha_i>0\)。以上问题来源于信息论,将功率分配给 \(n\) 个信道,变量 \(x_i\) 表示分配给第 \(i\) 个信道的发射功率,\(\log(\alpha_i+x_i)\) 是信道的通信能力或者通信速率,上述问题表述为将总功率分配给不同的信道,使得总的通信速率最大。对不等式约束 \(x^\ast\succeq 0\) 引入 Lagrange 乘子 \(\lambda^\ast\in R^n\),对等式约束 \(\mathbf{1}^Tx=1\) 引入一个乘子 \(v^\ast\in R\),我们得到如下 KKT 条件
\[ x^\ast\succeq 0, \quad \mathbf{1}^Tx^\ast=1, \quad \lambda^\ast\succeq 0, \quad \lambda^\ast_ix_i^\ast=0, \quad i=1,\cdots, n,\\\-1/(\alpha_i+x_i^\ast)-\lambda^\ast+v^\ast=0, \quad i=1,\cdots, n. \]
以上条件可以化简为
\[ x^\ast\succeq 0, \quad \mathbf{1}^Tx^\ast=1, \quad x_i^\ast(v^\ast-1/(\alpha_i+x_i^\ast))=0, \quad i=1,\cdots, n,\\\v^\ast\geq 1/(\alpha_i+x_i^\ast), \quad i=1,\cdots, n. \]
根据等式条件(松弛条件)进行分类:
综上我们有
\[ x^\ast= \begin{cases} 1/v^\ast-\alpha_i \quad v^\ast<1/\alpha_i\\\0 \quad v^\ast\geq 1/\alpha_i \end{cases} \]
更简洁地,\(x_i^\ast=\max\\{0, 1/v^\ast-\alpha_i\\}\),将 \(x^\ast\) 带入条件 \(\mathbf{1}^Tx^\ast=1\) 中得到以下关于 \(v^\ast\) 的方程
\[\sum_{i=1}^n\max\\{0, 1/v^\ast-\alpha_i\\}=1\]
容易知道以上方程存在唯一确定解,求解该解的方法称为“注水法”。求解出 \(v^\ast\) 后反带入以上方程中可以得到最优解 \(x^\ast\)。
如果强对偶性成立且存在一个对偶最优解,这时如果当对偶问题比原问题更容易求解时,比如说对偶问题可以解析求解或者有某些特殊的结构更容易分析,通过求解对偶问题具有重要意义。
扰动的问题:
考虑对优化问题 (BP) 进行扰动后的新优化问题
考虑以下(扰动)优化问题
\[
\begin{split}
&{\rm minimize}~~f_0(x)\\\&s.t.
\begin{cases}
f_i(x)\leq u_i, \quad i=1,\dots, m\\\h_i(x)=w_i, \quad i=1,\dots, p.
\end{cases}
\end{split}
\]
其中,变量 \(x\in R^n\)。如果 \(u_i=0, v_i=0\),则以上优化问题就是 (BP) 问题,如果 \(u_i\) 和 \(w_i\) 都大于零,则新问题是在 (BP) 问题上进行了放松,如果\(u_i\) 和 \(w_i\) 都小于零,则新问题是在 (BP) 问题上进行了收紧。
定义 \(p^\ast(u, w)\) 为以上扰动优化问题的最优值:
\[
p^\ast(u, w)=\inf\\{f_0(x)~|~\exists x\in\mathcal{D}, f_i(x)\leq u_i, i=1,\cdots, m,\\\\ h_i(x)=w_i, i=1,\cdots, p\\}
\]
一个重要不等式
设 \((\lambda^\ast, v^\ast)\) 是未扰动的 (BP) 问题的最优解,则对所有的 \(u\) 和 \(w\) 我们有
\[ p^\ast(u, v)\geq p^\ast (0, 0)-\lambda^{\ast T}u-v^{\ast T}w\tag{*} \]
证明:设 \(x\) 是任意的可行解,则根据强对偶性有
\[ \begin{split} p^\ast(0, 0)=g(\lambda^\ast, v^\ast)&\leq f_0(x)+\sum_{i=1}^m\lambda^\ast_if_i(x)+\sum_{i=1}^pv_i^\ast h_i(x)\\\&\leq f_0(x)+\lambda^{\ast T}u+v^{\ast T}w \end{split} \]
以上第一个不等式由 \(g(\lambda^\ast, v^\ast)\) 的定义得到;第二个不等式由 \(\lambda^\ast\succeq 0\) 以及扰动优化问题的约束得到。利用以上不等式可以直接得到:
\[ p^\ast(u, v)\geq p^\ast (0, 0)-\lambda^{\ast T}u-v^{\ast T}w \]
灵敏度的简单分析:
局部灵敏度分析:
如果 \(p^\ast(u, v)\) 在 \(u=0\) 和 \(v=0\) 处可微且强对偶性成立,最优对偶变量 \(\lambda^\ast\) 和 \(v^\ast\) 可以和 \(p^\ast\) 在 \(u=0, w=0\) 处的梯度联系起来:
\[
\lambda_i^\ast=-\frac{\partial p^\ast(0, 0)}{\partial u_i}, \quad v_i^\ast=-\frac{\partial p^\ast(0, 0)}{\partial w_i}
\]
证明:假设 \(p^\ast(u,w)\) 可微且强对偶性成立,对于扰动 \(u=te_i\),其中 \(e_i\) 是单位向量,它的第 \(i\) 个分量为1,我们有
\[\lim_{t\rightarrow 0}\frac{p^\ast(te_i, 0)-p^\ast(0, 0)}{t}=\frac{\partial p^\ast(0, 0)}{\partial u_i}\]
根据以上重要的不等式(*),当 \(t>0\) 时,下式成立
\[\frac{p^\ast(te_i, 0)-p^\ast(0, 0)}{t}\geq -\lambda^\ast_i\]
同样利用(*)不等式,\(t>0\) 时,下式成立
\[\frac{p^\ast(te_i, 0)-p^\ast(0, 0)}{t}\leq -\lambda^\ast_i\]
两边同时取 \(t\rightarrow 0\) 可以得到
\[\frac{\partial p^\ast(0, 0)}{\partial u_i}= -\lambda^\ast_i\]
利用同样的方法可以得到
\[\frac{\partial p^\ast(0, 0)}{\partial w_i}= -v^\ast_i\]
原文:https://www.cnblogs.com/hdawen/p/11617133.html