数学模型应用举例

前言

应用举例1

由集合之间的关系求解参数的取值范围模型

案例01【模型】若集合\(B=\{x\mid m+1\leq x\leq 1-2m \}\)，集合\(A=\{x\mid -2\leq x\leq 7\}\)，若\(A\subsetneqq B\)，求实数\(m\)的取值范围。

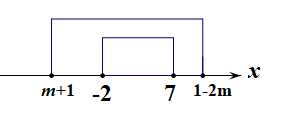
分析：自行画出草图可知，先列出条件\(\begin{cases}&m+1\leq-2\\&1-2m \ge 7\end{cases}\)，解得\(m\leq -3\)，

接下来验证\(m=-3\)是否满足题意。

当\(m=-3\)时，\(A=[-2，7]\)，\(B=[m+1，1-2m]=[-2，7]\)，此时\(A=B\)，不满足题意，舍去，

故实数\(m\)的取值范围为\(\{m\mid m<-3\}\)。

解后反思：本题目如上处理，则可以避免分类讨论；

模型应用1已知\(“\)命题\(p：(x-m)^2>3(x-m)\)\(”\)是\(“\)命题\(q：x^2+3x-4<0\)\(”\)成立的必要不充分条件,则实数\(m\)的取值范围为________.　

【解析】先化简命题\(p\)，由\((x-m)^2>3(x-m)\)，得到\(x^2-(2m+3)x+m^2+3m>0\)，

即\(x^2-(2m+3)x+m(m+3)>0\)，即\((x-m)[x-(m+3)]>0\)，

则有\(p：x>m+3\)或\(x<m；q：-4<x<1\)；

因为\(p\)是\(q\)成立的必要不充分条件，则\(\{x\mid-4<x<1\}\subseteq \{x\mid x>m+3或x<m\}\)，

所以\(m+3≤-4\)或\(m≥1\)，即\(m≤-7\)或\(m≥1\)，

故\(m\)的取值范围为\((-\infty，-7]\cup[1，+\infty)\)。

模型应用2已知函数\(f(x)=x^3+\cfrac{3}{2}x^2-6x+1\)在区间\([a，a+1]\)上单调递减，求参数\(a\)的取值范围。

法1：集合法，先用导数的方法求得函数\(f(x)\)的单调递减区间，\(f'(x)=3x^2+3x-6=3(x+2)(x-1)\)，

令\(f'(x)<0\)，解得\(x\in (-2，1)\)，即其单调递减区间为\([-2，1]\)，此处必须写成闭区间，否则会丢掉参数的个别取值。

而题设又已知函数在\([a，a+1]\)上单调递减，故\([a，a+1]\subseteq [-2，1]\)，即问题转化为集合的包含关系问题了。

此时只需要满足\(\left\{\begin{array}{l}{-2\leqslant a}\\{a+1\leqslant 1}\end{array}\right.\)，解得\(-2\leqslant a\leqslant 0\)，

故参数\(a\)的取值范围为\([-2，0]\)。

法2：导数法，由题设可知，\(f'(x)=3x^2+3x-6=3(x+2)(x-1)\)，由于函数在区间\([a，a+1]\)上单调递减，

则\(f'(x)=3(x+2)(x-1)\leq 0\)在区间\([a，a+1]\)上恒成立，则\(\left\{\begin{array}{l}{f'(a)\leqslant 0}\\{f'(a+1)\leqslant 0}\end{array}\right.\)

即\(\left\{\begin{array}{l}{3(a+2)(a-1)\leqslant 0}\\{3(a+3)a\leqslant 0}\end{array}\right.\)，解得\(\left\{\begin{array}{l}{-2\leqslant a\leqslant 1}\\{-3\leqslant a\leqslant 0}\end{array}\right.\)，则\(a\in [-2，0]\)。

应用举例2

模型【求解分段函数方程】【2016第三次全国大联考第15题】已知\(f(x)\)是定义在R上的奇函数，且当\(x<0\)时，\(f(x)=2x-1\)，若\(f(a)=3\)，求实数\(a\)的值。

分析：先由奇偶性求得\(x>0\)时，\(f(x)=2x+1\)，

即得到函数的解析式为\(f(x)=\begin{cases}2x-1&x<0\\0&x=0\\2x+1&x>0\end{cases}\)，且已知\(f(a)=3\)，求\(a\)的值，

等价转化为三个不等式组 \(\begin{cases}a<0\\2a-1=3\end{cases}\)，或\(\begin{cases}a=0\\0=3\end{cases}\)，或\(\begin{cases}a>0\\2a+1=3\end{cases}\)，

解得\(a=1\)。

模型应用1【2020届高三文科数学周末训练2用题】若函数\(f(x)=\left\{\begin{array}{l}{x+1，x\leqslant 0}\\{lnx，x>0，}\end{array}\right.\) 则函数\(y=f[f(x)]+1\)的零点的个数为______ 个。

【法1】：从数的角度求解；令\(f(x)=t\)，则函数的零点问题转化为方程\(f(t)=-1\)的解的个数问题；

即相当于已知\(f(x)=\left\{\begin{array}{l}{x+1，x\leqslant 0}\\{lnx，x>0，}\end{array}\right.\) 且\(f(t)=-1\)，求\(t\)的值；

则上述分段函数方程等价于\(\left\{\begin{array}{l}{t\leqslant 0}\\{t+1=-1}\end{array}\right.\) 或\(\left\{\begin{array}{l}{t> 0}\\{lnt=-1}\end{array}\right.\)

解得\(t=-2\)或者\(t=\cfrac{1}{e}\)，即\(f(x)=-2\)或者\(f(x)=\cfrac{1}{e}\)，到此题目又可以转化为

已知\(f(x)=\left\{\begin{array}{l}{x+1，x\leqslant 0}\\{lnx，x>0，}\end{array}\right.\) 且\(f(x)=-2\)，求\(x\)的值；可以仿上求解得到\(2\)个\(x\)的值；

或已知\(f(x)=\left\{\begin{array}{l}{x+1，x\leqslant 0}\\{lnx，x>0，}\end{array}\right.\) 且\(f(x)=\cfrac{1}{e}\)，求\(x\)的值；亦可以仿上求解得到\(2\)个\(x\)的值；

故所求的零点的个数为\(4\)个。

数学模型应用举例

原文：https://www.cnblogs.com/wanghai0666/p/11392760.html