1. 最小生成树定义

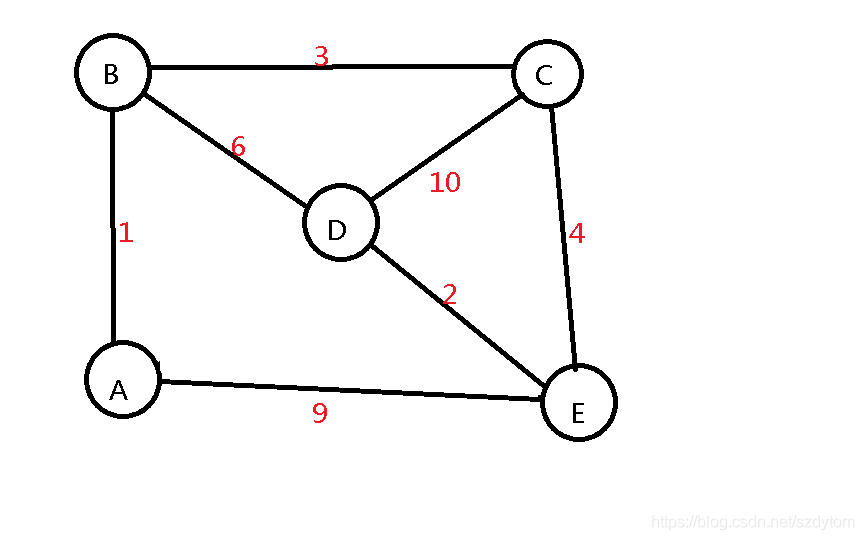
树是指没有环路的图，生成树就是指一个图上面删除一些边，使它没有环路。
最小生成树就是指生成树中边权之和最小的那一种。
上图的最小生成树就是这样：

2. Prim 算法

2.1. 算法流程

就以上图为例：

1. 先选择一个起始点，我们就以A为例。
2. 创建一个集合S，用来存储已经在树中间的点。开始时集合那只有点A，即 $S = {A}$。
3. 选择一个连通到集合S中一个点的最小边，其中它的另一个端点不在集合S中。以保证，最小生成树不会形成环。把这条边的不在S集合中的端点加到S集合中。（目前选边AB， $S = { A, B}$）
4. 重复步骤三，直到所有的点都在S集合中了。
5. 答案就是刚才所选的边的边权和啦。

时间复杂度： $$O(nm+m)$$

2.2. 优化

这个算法的时间的主要瓶颈就是在我们寻找那一条边的边权最小的时候，那么注意到这里其实是可以通过堆优化的。代码如下：

int ans = 0;
int index = 1;
h.push(point(0, 1));
while (index <= n) {
    int x = h.top().id, d = h.top().w;
    h.pop();
    if (S[x]) continue;
    S[x] = 1;
    ++index;
    ans += d;
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i].v, z = G[x][i].w;
        if (!S[y]) {
            h.push(point(z, y));
        }
    }
}

时间复杂度： $O(n\log m + m)$

3. kruskal 算法

3.1. 算法流程

还是以上图为例：

1. 首先第一步最开始，先给边排序。
2. 选择一个边权最小的边，判断它的两个端点是否原来已经连通，如果没有连通的话，就选这条边。以保证这个树上不会出现回路。
3. 重复步骤二，直到选出$n-1$条边为止.
4. 上面流程得到的树就是最小生成树。

时间复杂度：$O(n^2)$

3.2. 优化

算法的主要时间瓶颈就是在如何判断原来两个点已经连通，如果用DFS或者BFS的话，效率较低，所以我们这里使用并查集优化。

sort(E.begin(), E.end(), cmp);
int index = 1, np = 0;
int ans = 0;
while (index <= n - 1) {
    if (np >= E.size()) break;
    node now = E[np++];
    if (getf(now.u) == getf(now.v)) continue;
    ++index;
    ans += now.w;
    merage(now.u, now.v);
}

时间复杂度：$O(m \log m+m \alpha (n))$

==by szdytom ==

[C++]最小生成树

原文：https://www.cnblogs.com/szdytom/p/11622045.html