file: tensorflow/python/training/learning_rate_decay.py
神经网络中通过超参数 learning rate,来控制每次参数更新的幅度。学习率太小会降低网络优化的速度,增加训练时间;学习率太大则可能导致可能导致参数在局部最优解两侧来回振荡,网络不能收敛。
tensorflow 定义了很多的 学习率衰减方式:
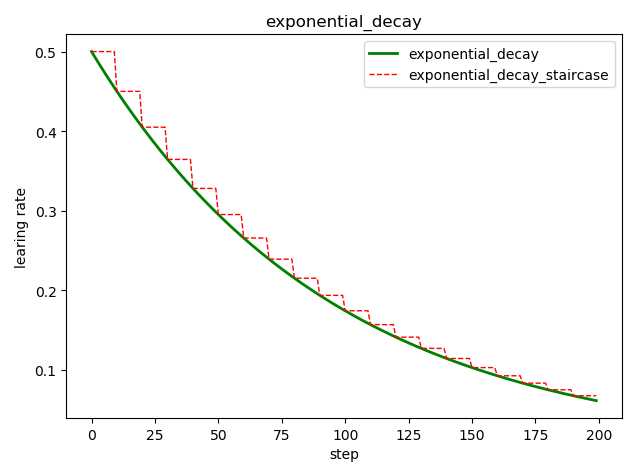
指数衰减是比较常用的衰减方法,学习率是跟当前的训练轮次指数相关的。
tf.train.exponential_decay( learning_rate, # 初始学习率 global_step, # 当前训练轮次 decay_steps, # 衰减周期 decay_rate, # 衰减率系数 staircase=False, # 定义是否是阶梯型衰减,还是连续衰减,默认是 False name=None ) ‘‘‘ decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps) ‘‘‘
示例代码:

import tensorflow as tf import matplotlib.pyplot as plt style1 = [] style2 = [] N = 200 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(N): # 标准指数型衰减 learing_rate1 = tf.train.exponential_decay( learning_rate=0.5, global_step=step, decay_steps=10, decay_rate=0.9, staircase=False) # 阶梯型衰减 learing_rate2 = tf.train.exponential_decay( learning_rate=0.5, global_step=step, decay_steps=10, decay_rate=0.9, staircase=True) lr1 = sess.run([learing_rate1]) lr2 = sess.run([learing_rate2]) style1.append(lr1) style2.append(lr2) step = range(N) plt.plot(step, style1, ‘g-‘, linewidth=2, label=‘exponential_decay‘) plt.plot(step, style2, ‘r--‘, linewidth=1, label=‘exponential_decay_staircase‘) plt.title(‘exponential_decay‘) plt.xlabel(‘step‘) plt.ylabel(‘learing rate‘) plt.legend(loc=‘upper right‘) plt.tight_layout() plt.show()
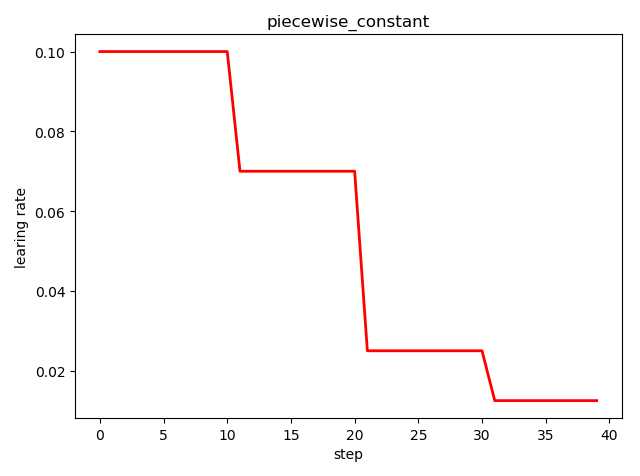
tf.train.piecewise_constant_decay( x, # 当前训练轮次 boundaries, # 学习率应用区间 values, # 学习率常数列表 name=None ) ‘‘‘ learning_rate value is `values[0]` when `x <= boundaries[0]`, `values[1]` when `x > boundaries[0]` and `x <= boundaries[1]`, ..., and values[-1] when `x > boundaries[-1]`. ‘‘‘
示例代码:

import tensorflow as tf import matplotlib.pyplot as plt boundaries = [10, 20, 30] learing_rates = [0.1, 0.07, 0.025, 0.0125] style = [] N = 40 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(N): learing_rate = tf.train.piecewise_constant(step, boundaries=boundaries, values=learing_rates) lr = sess.run([learing_rate]) style.append(lr) step = range(N) plt.plot(step, style, ‘r-‘, linewidth=2) plt.title(‘piecewise_constant‘) plt.xlabel(‘step‘) plt.ylabel(‘learing rate‘) plt.tight_layout() plt.show()
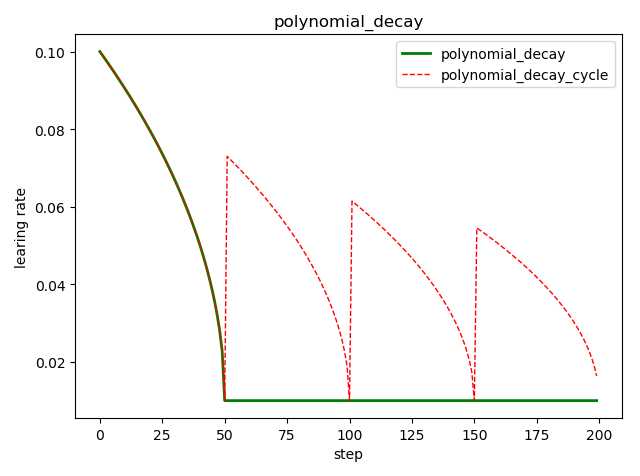
tf.train.polynomial_decay( learning_rate, # 初始学习率 global_step, # 当前训练轮次 decay_steps, # 大衰减周期 end_learning_rate=0.0001, # 最小的学习率 power=1.0, # 多项式的幂 cycle=False, # 学习率是否循环 name=None) ‘‘‘ global_step = min(global_step, decay_steps) decayed_learning_rate = (learning_rate - end_learning_rate) * (1 - global_step / decay_steps) ^ (power) + end_learning_rate ‘‘‘
示例代码:

import tensorflow as tf import matplotlib.pyplot as plt style1 = [] style2 = [] N = 200 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(N): # cycle=False learing_rate1 = tf.train.polynomial_decay( learning_rate=0.1, global_step=step, decay_steps=50, end_learning_rate=0.01, power=0.5, cycle=False) # cycle=True learing_rate2 = tf.train.polynomial_decay( learning_rate=0.1, global_step=step, decay_steps=50, end_learning_rate=0.01, power=0.5, cycle=True) lr1 = sess.run([learing_rate1]) lr2 = sess.run([learing_rate2]) style1.append(lr1) style2.append(lr2) steps = range(N) plt.plot(steps, style1, ‘g-‘, linewidth=2, label=‘polynomial_decay‘) plt.plot(steps, style2, ‘r--‘, linewidth=1, label=‘polynomial_decay_cycle‘) plt.title(‘polynomial_decay‘) plt.xlabel(‘step‘) plt.ylabel(‘learing rate‘) plt.legend(loc=‘upper right‘) plt.tight_layout() plt.show()
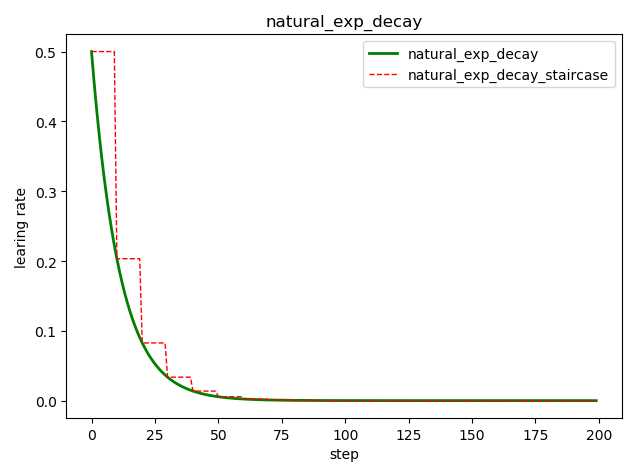
tf.train.natural_exp_decay( learning_rate, # 初始学习率 global_step, # 当前训练轮次 decay_steps, # 衰减周期 decay_rate, # 衰减率系数 staircase=False, # 定义是否是阶梯型衰减,还是连续衰减,默认是 False name=None ) ‘‘‘ decayed_learning_rate = learning_rate * exp(-decay_rate * global_step) ‘‘‘
示例代码:

import tensorflow as tf import matplotlib.pyplot as plt style1 = [] style2 = [] N = 200 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(N): # 标准指数型衰减 learing_rate1 = tf.train.natural_exp_decay( learning_rate=0.5, global_step=step, decay_steps=10, decay_rate=0.9, staircase=False) # 阶梯型衰减 learing_rate2 = tf.train.natural_exp_decay( learning_rate=0.5, global_step=step, decay_steps=10, decay_rate=0.9, staircase=True) lr1 = sess.run([learing_rate1]) lr2 = sess.run([learing_rate2]) style1.append(lr1) style2.append(lr2) step = range(N) plt.plot(step, style1, ‘g-‘, linewidth=2, label=‘natural_exp_decay‘) plt.plot(step, style2, ‘r--‘, linewidth=1, label=‘natural_exp_decay_staircase‘) plt.title(‘natural_exp_decay‘) plt.xlabel(‘step‘) plt.ylabel(‘learing rate‘) plt.legend(loc=‘upper right‘) plt.tight_layout() plt.show()
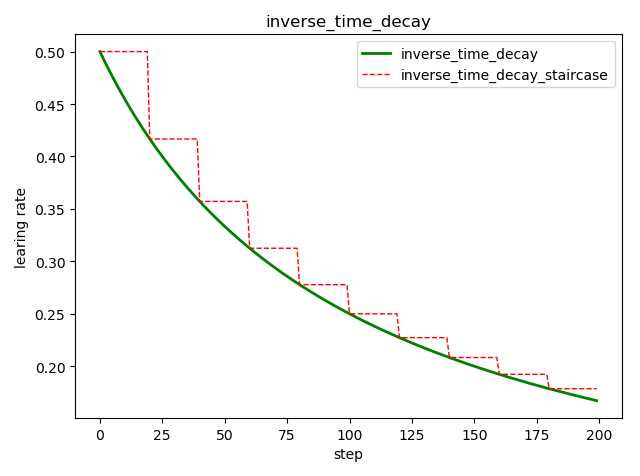
tf.train.inverse_time_decay( learning_rate, # 初始学习率 global_step, # 当前训练轮次 decay_steps, # 衰减周期 decay_rate, # 衰减率系数 staircase=False, # 定义是否是阶梯型衰减,还是连续衰减,默认是 False name=None ) ‘‘‘ decayed_learning_rate = learning_rate / (1 + decay_rate * global_step / decay_step) ‘‘‘
示例代码:

import tensorflow as tf import matplotlib.pyplot as plt style1 = [] style2 = [] N = 200 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(N): # 标准指数型衰减 learing_rate1 = tf.train.inverse_time_decay( learning_rate=0.5, global_step=step, decay_steps=20, decay_rate=0.2, staircase=False) # 阶梯型衰减 learing_rate2 = tf.train.inverse_time_decay( learning_rate=0.5, global_step=step, decay_steps=20, decay_rate=0.2, staircase=True) lr1 = sess.run([learing_rate1]) lr2 = sess.run([learing_rate2]) style1.append(lr1) style2.append(lr2) step = range(N) plt.plot(step, style1, ‘g-‘, linewidth=2, label=‘inverse_time_decay‘) plt.plot(step, style2, ‘r--‘, linewidth=1, label=‘inverse_time_decay_staircase‘) plt.title(‘inverse_time_decay‘) plt.xlabel(‘step‘) plt.ylabel(‘learing rate‘) plt.legend(loc=‘upper right‘) plt.tight_layout() plt.show()
tf.train.cosine_decay( learning_rate, # 初始学习率 global_step, # 当前训练轮次 decay_steps, # 衰减周期 alpha=0.0, # 最小的学习率 name=None ) ‘‘‘ global_step = min(global_step, decay_steps) cosine_decay = 0.5 * (1 + cos(pi * global_step / decay_steps)) decayed = (1 - alpha) * cosine_decay + alpha decayed_learning_rate = learning_rate * decayed ‘‘‘
改进的余弦衰减方法还有:
线性余弦衰减,对应函数 tf.train.linear_cosine_decay()
噪声线性余弦衰减,对应函数 tf.train.noisy_linear_cosine_decay()
示例代码:

import tensorflow as tf import matplotlib.pyplot as plt style1 = [] style2 = [] style3 = [] N = 200 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(N): # 余弦衰减 learing_rate1 = tf.train.cosine_decay( learning_rate=0.1, global_step=step, decay_steps=50) # 线性余弦衰减 learing_rate2 = tf.train.linear_cosine_decay( learning_rate=0.1, global_step=step, decay_steps=50) # 噪声线性余弦衰减 learing_rate3 = tf.train.noisy_linear_cosine_decay( learning_rate=0.1, global_step=step, decay_steps=50, initial_variance=0.01, variance_decay=0.1, num_periods=0.2, alpha=0.5, beta=0.2) lr1 = sess.run([learing_rate1]) lr2 = sess.run([learing_rate2]) lr3 = sess.run([learing_rate3]) style1.append(lr1) style2.append(lr2) style3.append(lr3) step = range(N) plt.plot(step, style1, ‘g-‘, linewidth=2, label=‘cosine_decay‘) plt.plot(step, style2, ‘r--‘, linewidth=1, label=‘linear_cosine_decay‘) plt.plot(step, style3, ‘b--‘, linewidth=1, label=‘linear_cosine_decay‘) plt.title(‘cosine_decay‘) plt.xlabel(‘step‘) plt.ylabel(‘learing rate‘) plt.legend(loc=‘upper right‘) plt.tight_layout() plt.show()
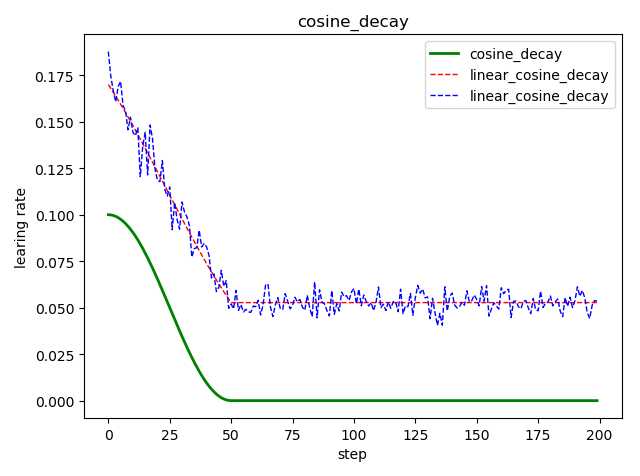
这是在 fast.ai 中强推的衰减方式
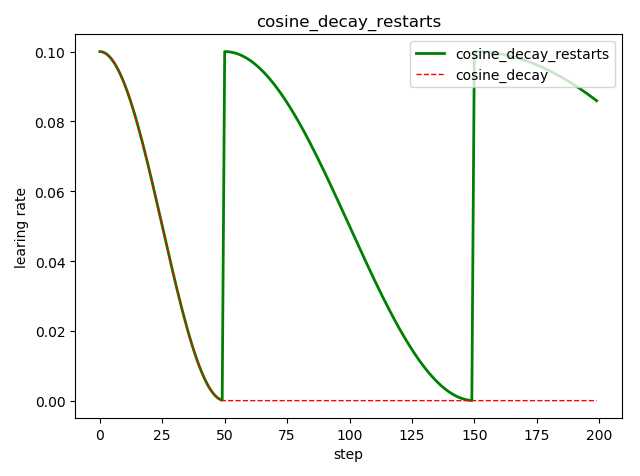
tf.train.cosine_decay_restarts( learning_rate, # 初始学习率 global_step, # 当前训练轮次 first_decay_steps, # 首次衰减周期 t_mul=2.0, # 随后每次衰减周期倍数 m_mul=1.0, # 随后每次初始学习率倍数 alpha=0.0, # 最小的学习率 name=None ) ‘‘‘ See [Loshchilov & Hutter, ICLR2016], SGDR: Stochastic Gradient Descent with Warm Restarts. https://arxiv.org/abs/1608.03983 The learning rate multiplier first decays from 1 to `alpha` for `first_decay_steps` steps. Then, a warm restart is performed. Each new warm restart runs for `t_mul` times more steps and with `m_mul` times smaller initial learning rate. ‘‘‘
示例代码:

import tensorflow as tf import matplotlib.pyplot as plt style1 = [] style2 = [] N = 200 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(N): # 余弦衰减 learing_rate1 = tf.train.cosine_decay_restarts( learning_rate=0.1, global_step=step, first_decay_steps=50, ) # 循环余弦衰减 learing_rate2 = tf.train.cosine_decay( learning_rate=0.1, global_step=step, decay_steps=50) lr1 = sess.run([learing_rate1]) lr2 = sess.run([learing_rate2]) style1.append(lr1) style2.append(lr2) step = range(N) plt.plot(step, style1, ‘g-‘, linewidth=2, label=‘cosine_decay_restarts‘) plt.plot(step, style2, ‘r--‘, linewidth=1, label=‘cosine_decay‘) plt.title(‘cosine_decay_restarts‘) plt.xlabel(‘step‘) plt.ylabel(‘learing rate‘) plt.legend(loc=‘upper right‘) plt.tight_layout() plt.show()
TensorFlow使用记录 (三): Learning rate
原文:https://www.cnblogs.com/xuanyuyt/p/11621532.html