struct PAM_Trie
{
int ch[30]; //字典树
int fail; //fail指针,指向当前节点所表示的回文串的最长回文后缀(不包括自己)
int len; //len表示当前节点表示的回文串的长度
int num; //以第i个字符结尾的回文串的个数
};
struct PAM
{
PAM_Trie b[maxn]; //字典树
int len_str; //字符串的长度
int last; //上一次插入的节点编号
int cnt; //总的节点的个数
int s[maxn]; //原字符串对应的ASCII码
char c[maxn]; //原字符串
}回文自动机和\(trie\)树一样,将信息存储在边上。
回文自动机的每一个节点(除了根)都表示一个回文串,一个节点向下连一条边\(ch\)代表在他两边各自加一个字符,即\(len+=2\)。
如图所示加深理解:
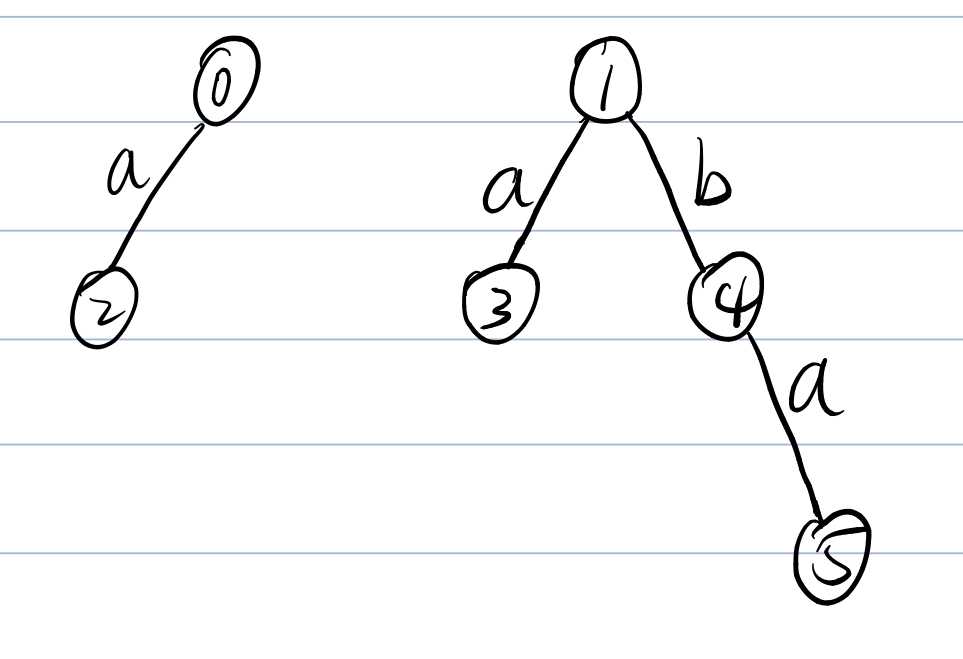
如图所示,他每个节点所代表的回文串分别是(从\(2\)到\(5\)):\(aa,a,b,aba\)。(这里这张图只是增加感性认识,真实构建可能不会出现此形态的自动机。)
因为\(1\)号树是存长度为奇数的回文串,每次操作又要\(len+=2\),为了减少特判,相信这里大家也能明白这里为什么\(len(1)\)的初值为\(-1\)。
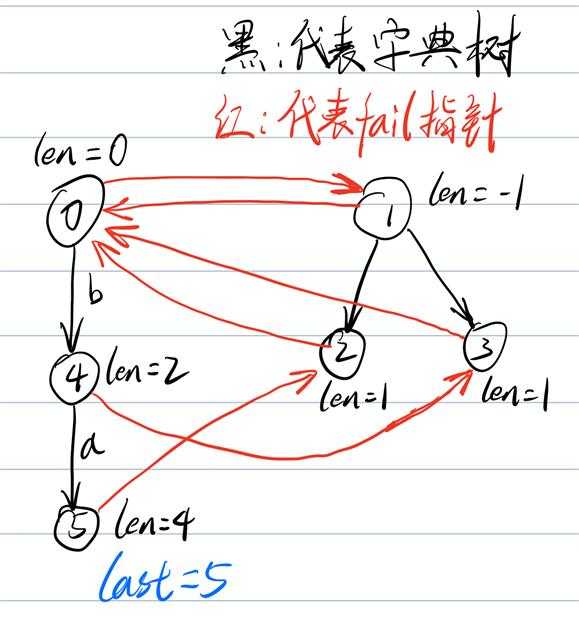
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 10;
struct PAM_Trie
{
int ch[30]; //字典树
int fail; //fail指针,指向当前节点所表示的回文串的最长回文后缀(不包括自己)
int len; //len表示当前节点表示的回文串的长度
int num; //以第i个字符结尾的回文串的个数
};
struct PAM
{
PAM_Trie b[maxn]; //字典树
int len_str; //字符串的长度
int last; //上一次插入的节点编号
int cnt; //总的节点的个数
int s[maxn]; //原字符串对应的ASCII码
char c[maxn]; //原字符串
PAM() //构造函数自动调用
{
b[0].len = 0; //初始状态下长度为0
b[1].len = -1; //1号节点len=-1方便接下来的操作
b[0].fail = 1; //0号节点fail指向1号节点
b[1].fail = 0; //1号节点fail指向0号节点
last = 0; //last初始值为0
cnt = 1; //cnt=1是因为初始的时候有1号结点
//插入的时候可用++cnt
}
//读入字符串
void read()
{
scanf("%s", c + 1);
len_str = strlen(c + 1);
}
//寻找当前
int get_fail(int las, int i)
{
//假如说我刚进来
//las是上一次的插入的节点
//我们又知道len(las)代表以las这个点的回文串
//所以这是一段中间是回文串的字符串
//我们只需要验证两端,也就是i-len(las)-1和i如果相等
//则说明i这个点的最长回文串长度是len(las)+2
//不匹配的话,las就跳转到fail指针指向的节点接着找
while(s[i-b[las].len-1] != s[i])
las = b[las].fail;
return las;
}
//新建节点
void ins(int i)
{
int p = get_fail(last, i);
//找当前节点两端能匹配的那个位置
if(!b[p].ch[s[i]]) //如果当前trie图里没有这个节点
{
//新节点的长度是前后各自拼接了一个字符
//所以当前节点的长度比原来多2
b[++cnt].len = b[p].len + 2;
//为当前位置寻找fail指针
int tmp = get_fail(b[p].fail, i);
b[cnt].fail = b[tmp].ch[s[i]];
//更新答案 同时给trie图中的该节点赋值
b[cnt].num = b[b[cnt].fail].num + 1;
b[p].ch[s[i]] = cnt;
}
//更新last(上一次插入的节点)
last = b[p].ch[s[i]];
}
//这题题目要求第i个位置答案是k,第i+1个位置代表的
//字符就变成了(c-97+k) % 26 + 97
void solve()
{
int k = 0;
s[0] = int('#'); //这里写啥都好, 只要input里不会出现就行
for(int i = 1; i <= len_str; i++)
{
c[i] = (c[i] - 97 + k) % 26 + 97;
s[i] = c[i] - 'a';
ins(i); //在自动机中插入结点
printf("%d ", b[last].num);
//输出以当前字符结尾的回文串数量
k = b[last].num; //跟随题意
}
}
}P;
int main()
{
P.read();
P.solve();
return 0;
}
原文:https://www.cnblogs.com/zxytxdy/p/11626213.html