得分:10
分段
题目描述
我们都知道如果一个字符串正着读和倒着读是同样的,则称为回文串。长度为偶数的回文
串称为偶回文串。比如 00, 10100101 是偶回文串, 010, 100100 都不是偶回文串。
如果一个串 s 可以被写成若干个字符串的连接, s = p1p2 : : : ; pm,且满足每个串 pi 都是偶
回文串,那么我们称 s 是美丽的。
现在输入一个 01 串 t,你可以选择(也可以不选)将其中的某几位反转 (即将 0 变成 1,
将 1 变成 0)。反转第 i 位需要花费 wi 的代价 (wi ≥ 0)。 (最左边的是第 1 位,最右边的是第 n
位) 你需要花费最小的总代价将 t 变成一个美丽的串。请求出最小的总代价。保证串 t 的长度
n 是偶数。
输入
第一行一个整数 n。表示字符串 t 的长度。
第二行一个字符串 t。
第三行包含 n 个空格隔开的整数 w1; : : : ; wn。
输出
输出一行最小总代价。
样例输入
8
00101011
8 7 6 5 4 3 2 1
样例输出
5
样例解释
改第 6 位和第 7 位,得到 00 + 101101.
数据规模与约定
共有 10 个数据。
对于数据 1, n ≤ 6。
对于数据 2,3, n ≤ 40。
对于数据 4,5,6, n ≤ 300。
对于所有数据 1 ≤ n ≤ 2000; 0 ≤ wi ≤ 100000. 保证 n 是一个偶数
分析:
分段
先用 O(n2) 时间预处理出把每段区间 [i; j] 变成偶回文串需要的最小代价。然后就可以 dp
了, f[i] 表示把 i 长度的前缀弄成美丽的串的总代价,然后枚举分割进行转移。复杂度 O(n2)。
1.考虑所有的偶数区间都可以转化为一个偶回文串,首先我们可以用O(n^2)的时间复杂度预处理出将[l,r]区间转化
为偶回文串的最小代价,考虑用记忆化搜索进行预处理(这样可以不用考虑递推顺序),写成函数get_cost(l,r)
注意保存状态
lnt get_cost(lnt l,lnt r)//获取[l,r]内的最小代价
{
if(cost[l][r]!=-1)return cost[l][r];//如果[l,r]内的代价
//已经求解出来,直接返回记忆化的值
if(r<l)return 0;//如果这个区间不符合实际情况,直接返回
if(t[l]==t[r])cost[l][r]=get_cost(l+1,r-1);//
//如果这个字符串的区间端点相同,那么可以由[l+1,r-1]区间的
//信息得到
//如果端点不同,那么就取任意改变一个端点的最小代价计入对答案
//的贡献之中去
else cost[l][r]=get_cost(l+1,r-1)+min(w[l],w[r]);//
return cost[l][r];//返回cost[l][r]的值
}
2.在得到每个修改每个区间的代价后:
思路1:考虑将其当成背包来做,定义f[i]表示从1->i的数列改成美丽数列所需要的最小代价!
遍历所有可能的组合方案:
注意两点,其一是便利i时的增量为2!保证增长单位是最小的偶区间,其二是j需要从0开始枚举,
get_cost函数求出[j,i-1]的值!
for(int i=2;i<=n;i+=2)
for(int j=0;j<=i;j+=2)
f[i]=min(f[i],f[j]+get_cost(j,i-1))
3.考虑转化为Dijkstra求最短路!(n^2预处理,把每个区间的左右端点连一条边,求1到n+1的最短路)
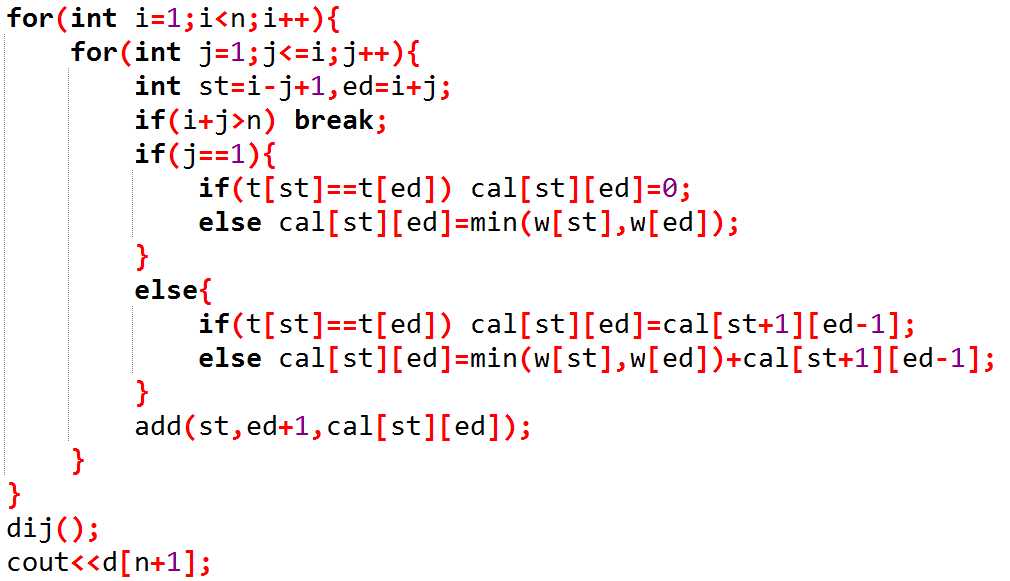
2019.10.6 Oi模拟赛总结T1:区间DP预处理+前缀DP
原文:https://www.cnblogs.com/little-cute-hjr/p/11628358.html