

注意矢量只有长度和方向,没有位置!也就是说矢量可以任意的平移!

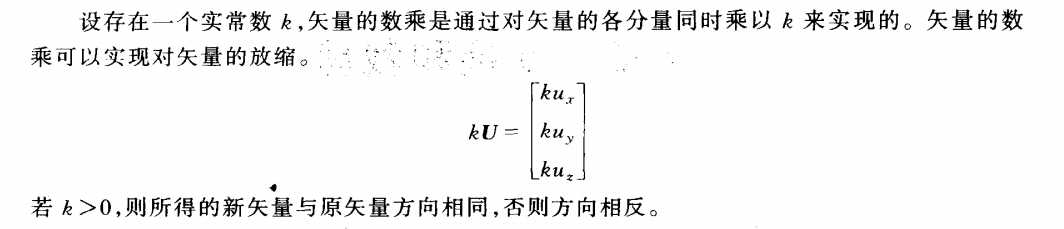

有时候经常需要缩放矢量,使其长度为1,这个过程称为矢量的归一化!

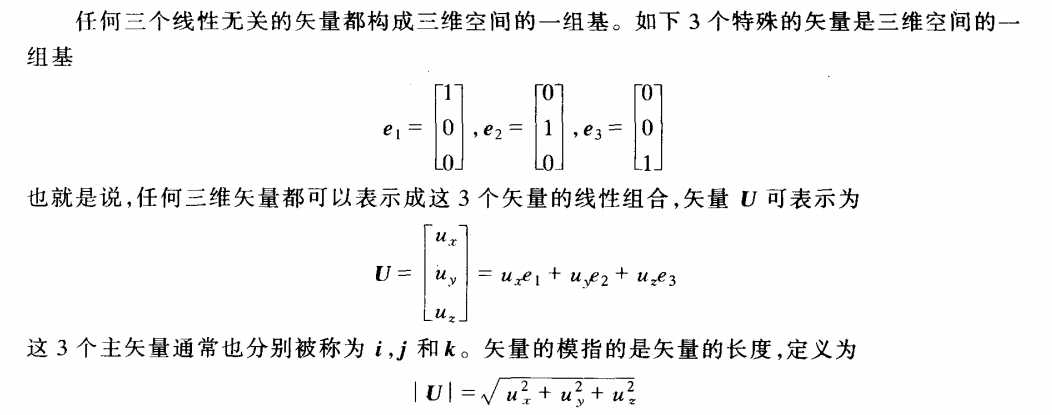
矢量点乘的结果是标量。
点乘最重要的应用就是计算两个矢量的夹角,或者两条直线的夹角。
由于两个向量的点乘和它们之间夹角的余弦成正比,可以得出以下关于两个非零向量夹角与点乘的关系:
点乘在新闻分类中的应用
新闻分类是把相似的新闻放在一类中,如何设计一个算法来算出任意两篇新闻的相似性?
用一个向量来描述一篇新闻
当夹角的余弦接近1时,两条新闻相似,从而可以归为一类:夹角的余弦越小,两条新闻越不相关!!!

矢量叉乘的结果是矢量,得到的新矢量与原来的两个矢量都相交!!!
获得的新矢量的大小,是下面平行四边形的面积


只有矩阵的行数和列数都相等时,才能进行加法运算。
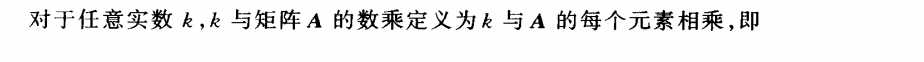

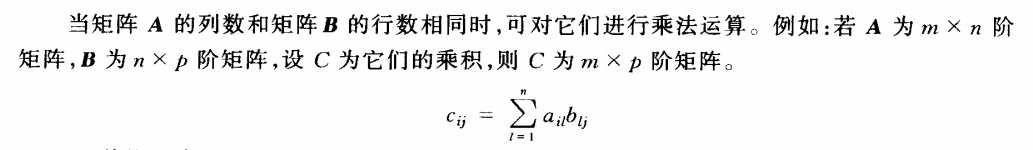
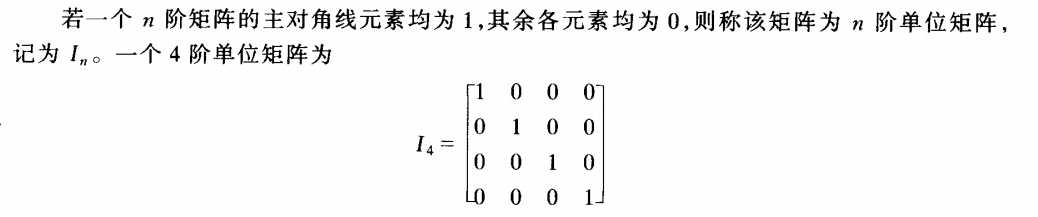



原文:https://www.cnblogs.com/wkfvawl/p/11643976.html