
题意:求for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) sum += f[i][j]; f[i][j]表示在序列从 i 位乘到第 j 位所形成的新的数的 不同质因子的个数.
思路:说是话,拿到题还是一开始想着能不能进行递推,比如先将每一个数进行 质因分解 然后用set不断更新统计个数来求和。但这样无论怎样都无法优化 (n^2) ,所以换思路再想。
就忽然想到了以前有一道做过的原题,题意是:给定一个长度为n的序列,然后求出每一个子区间不同数的个数和。而这一道题就是组合计数,计算每一个位置上的值对最后区间计数所产生的贡献。
而这道题类似,略微修改即是每一个位置上不只一个值(分解可能得到多个质因子),所以就用set来存放。
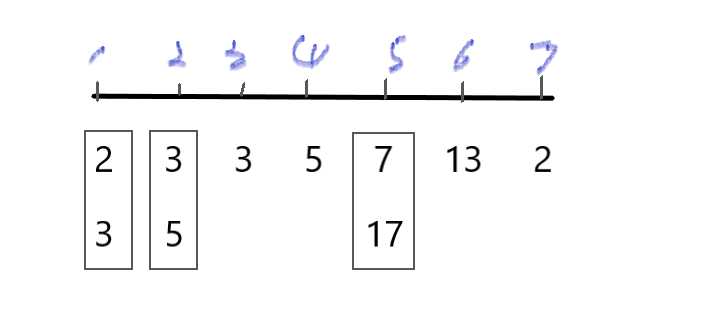
上面这幅图,坐标轴上表示坐标,坐标轴下表示每个位置set所存放对应数的质因子数。比如我们对所有位置的5的贡献值进行计算。
位置坐标2:由于这个5要产生贡献,即其左边起始下标要从 1 开始,直到它本身的坐标 2. 其右边的开始坐标从它本身开始 2 一直延申到坐标轴右端. 所以 左 x 右 = (2-0) x (7-2+1) = 10;
位置坐标4:要使这个位置的5产生贡献,由于我们对上一个5右边所有区间进行了计算,所以在计算这个5的贡献的时候我们要从它上一个5的位置的下一位开始到它本身,即从 3-4,而其右端也是延申到右端点,所以 (4-2) x (7-4+1) = 8;
所以计算某个数的贡献,即 其左边第一个出现的下一位开始到他本身位置为左端点取值范围,从他本身开始到坐标轴右端点为其区间右端点取值范围,而左乘以右则为所有区间贡献总和。
#include <bits/stdc++.h> #define IOS ios::sync_with_stdio(0); cin.tie(0); #define mp make_pair using namespace std; typedef long long ll; typedef unsigned long long ull; typedef pair<int, int> pii; const double Pi = acos(-1.0); const double esp = 1e-9; const int inf = 0x3f3f3f3f; const int maxn = 1e5+7; const int maxm = 1e6+7; const int mod = 1e9+7; //所有模板默认 prime[],powe[]从下标0开始取 const int MAXL = 1e6+7; //int phi[MAXL];//欧拉函数 int tot; int prim[MAXL];//素数表 int cnt; int vis[MAXL]; //int powe[MAXL];//质数幂 int cur; int pp[maxm]; set<int>qq[maxm]; set<int>::iterator it; int a[maxm]; int getPrime(){ int i ,j; int cnt = 0; memset(vis,0,sizeof(0)); vis[0] = vis[1] = 1; for(i=2;i<=MAXL;++i) { if(!vis[i]) vis[i]= prim[cnt++]= i; for(j=0;j<cnt&&i*prim[j]<=MAXL;++j){ vis[i*prim[j]] = 1; if(i%prim[j]==0) break; } } return cnt; } int getfac(int n,int cnt,int pos){ for(int i=0;prim[i]*prim[i]<=n;i++){ if(n%prim[i]==0) { qq[pos].insert(prim[i]); pp[prim[i]] = 0; while(n%prim[i]==0) n /= prim[i]; } } if(n>1) qq[pos].insert(n); } int main(){ int n; scanf("%d",&n); cnt = getPrime(); for(int i=1;i<=n;i++){ scanf("%d",a+i); getfac(a[i],cnt,i); } ll sum = 0; for(int i=1;i<=n;i++){ for(it = qq[i].begin();it != qq[i].end(); it++){ int tmp = *it; int k = pp[tmp]; pp[tmp] = i; sum += (ll) (i-k)*(n-i+1); } } printf("%lld\n",sum); }
原文:https://www.cnblogs.com/Tianwell/p/11668124.html