共轭先验（conjugate prior）：
共轭是贝叶斯理论中的一个概念，共轭一般指的是 先验分布与似然函数之间共轭；而共轭的结局是让 后验概率分布（根据贝叶斯公式，后验概率分布正?于先验概率分布和似然函数的乘积）拥有与先验分布相同的函数形式，简单说就是服从同种形式的分布。
之所以采用共轭先验的原因是可以使得先验分布和后验分布的形式相同，这样一方面合符人的直观（它们应该是相同形式的），另外一方面是可以形成一个先验链，即现在的后验分布 p(θ|x) 可以作为下一次计算的先验分布 p(θ)，如果形式相同，就可以形成一个链条。
似然函数：
在贝叶斯公式里，p(x|θ) 叫做似然函数。会发现和之前学习的最大似然估计中的 L(θ|x) 不一样。但事实上在贝叶斯公式里，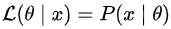
。解释：参数 θ 在给定观测值 x 的情况下的似然函数等于，在给定参数为 θ 的情况下，取 x 的概率。注意：P(x|θ) 处的竖杠并不表示条件概率，仅仅是一种取该值的含义。
概率密度函数：
概率分布函数，给出取值小于某个值的概率，是
概率质量函数的累加和 F(x)=P(xi<x)=sum(P(x1),P(x2),……,P(x))（对于离散型变量）；
或对概率密度函数f(x)求积分（对于连续型变量）。
概率质量函数用于描述离散型变量，即用函数形式给出每个取值发生的概率，P(x)（x=x1，x2，x3，……）。
概率密度函数用于描述连续型变量，概率密度函数f(x)在点a处取值，不是时间{x=a}的概率。但是，该值越大，X在a点附近取值的概率越大。概率密度函数只能用于描述某区间的概率，且等于这个区间内对f(x)求积分。
二项分布(p指事件成功的概率，下同)：
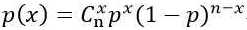
伯努利分布/0-1分布为二项分布在n=1时的特例。
几何分布：
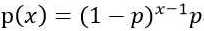
泊松分布(x代表要计算的给定时间范围内事件发生的次数，u代表给定时间范围内事件发生的平均次数)：
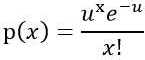
均匀分布(一个连续随机变量X在区间[a,b]上服从均匀分布，记作X∼Uniform(a,b))：
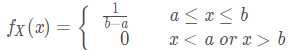
https://www.cnblogs.com/simayuhe/p/5143538.html
https://blog.csdn.net/baimafujinji/article/details/51374202
https://www.cnblogs.com/aaronsw/p/7071124.html
https://www.jianshu.com/p/0cfc3204af77
http://www.360doc.com/content/17/1231/22/9200790_718001949.shtml
原文：https://www.cnblogs.com/boceng/p/11668172.html