\(Description\)

题面

给你一颗\(n\)个节点带权的树以及\(m\)条路径端点，你可以将一条边的权值设为\(0\)，要求使得操作后\(m\)条路径中的最长路径最短

这道题有很多解法，我在复习一种算法后更新一种

\(Solution1\)

二分+贪心+\(LCA\)+树上差分
这道题显然不是裸的树上差分，但需要树上差分进行\(check\)操作
首先我们预处理出\(m\)条路径的长度，这个是可以使用前缀和\(O(n)\)求的，具体方法是在\(dfs\)过程中记录从根节点到\(u\)的距离\(f[u]\)，求一条路径\(u,v\)的长度只需要
\(dis[u]+[v]-2*dis[lca(u,v)]\)即可，画个图就很显然了，这是很重要的前缀和思想

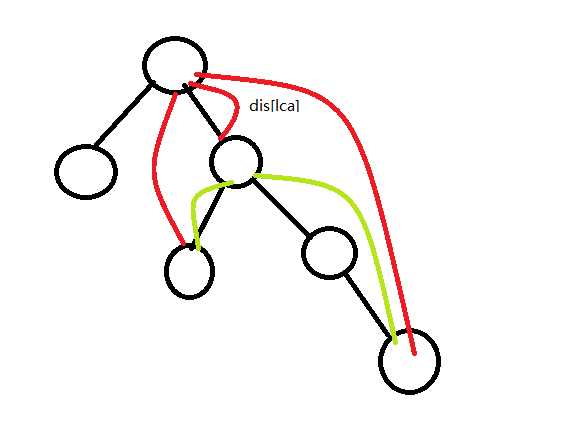
看到题目中"使得最大距离最小"这句话，显然需要二分答案，我们二分操作后（将一条边权值归零）的最大距离，关键在于如何写\(check\)
考虑记录每一条长度比\(mid\)大的路径，用边差分记录一下，假设这样的路径有\(cnt\)条，那么显然这\(cnt\)条路径需要删除一条公共边的权值。
所以我们\(dfs\)一遍，对差分数组求前缀和

假设没有一条边被经过\(cnt2\)次，说明这\(cnt\)条路径没有公共边，显然不能通过删一条边来达到\(mid\)，直接\(return\ false\)；
若有多条边被经过\(cnt2\)次，贪心取最大的一条即可，因为删去的权值越大越能接近合法（显然）。
最后将\(cnt\)条路径长度的最大值减去找到的最大公共边，如果仍然\(>mid\)则\(return\ false\)，否则\(return \ true\)

总结

1.在\(dfs1\)（预处理\(lca\)）的过程中处理到根的距离
2.二分最大长度
3.对大于二分值的路径差分，\(dfs2\)寻找是否可以通过删去一条公共边使得最大长度\(<mid\)
时间复杂度\(O((n+m)logn)\)，由于倍增\(LCA\)常数比较大，在当年\(noip\)是拿不到满分的，但是\(luogu\)数据比较水\(AC\)了
后面会介绍其他能通过此题（常数比较小）的算法

\(Code1\)

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define re register
#define maxn 300010
using namespace std;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct Edge{
    int v,w,nxt;
}e[maxn<<2];
int maxx,cnt2,tmp2,es[maxn],guide;
int fr[maxn],to[maxn],num[maxn],sums2;
int a[maxn],z,x,y,cc[maxn];
int cf[maxn],ans,val[maxn],tmp,dep[maxn],head[maxn],cnt,dis[maxn];
int n,m,lg[maxn],num2,f[maxn][23];
inline void add(int u,int v,int w)
{
    e[++cnt].v=v;
    e[cnt].w=w;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
void pre()
{
    for(re int i=1,num2=0;i<=n;i*=2) lg[i]=num2++; 
    for(re int i=1;i<=n;++i) if(!lg[i]) lg[i]=lg[i-1];
}
void dfs(int u,int fa,int w)
{;
    dep[u]=dep[fa]+1;
    f[u][0]=fa;
    dis[u]=dis[fa]+w;//预处理 
    es[u]=w;//将边权固定到点上 
    for(int i=1;(1<<i)<=dep[u];++i)
     f[u][i]=f[f[u][i-1]][i-1];
    for(int i=head[u];i;i=e[i].nxt)
    {
        int ev=e[i].v;
        if(ev!=fa) dfs(ev,u,e[i].w);
    }
}
int lca(int x,int y)
{
    if(dep[x]<dep[y]) swap(x,y);
    for(re int i=lg[dep[x]-dep[y]];i>=0;--i)
    {
        if(dep[f[x][i]]<dep[y]) continue;
        x=f[x][i];
    }
    if(x==y) return x;
    for(re int i=lg[dep[x]-1];i>=0;--i)
    {
        if(f[x][i]==f[y][i]) continue;
        x=f[x][i],y=f[y][i];
    }
    return f[x][0];
}
void dfs2(int u,int fa)
{
    for(int i=head[u];i;i=e[i].nxt)
    {
        //int sums=0;
        int ev=e[i].v;
        if(ev==fa) continue;
        dfs2(ev,u);
        a[u]+=a[ev]; 
    }
    a[u]+=cf[u];//更新当前的前缀和 
    if(a[u]>=cnt2)
    {
        guide=max(guide,es[u]);
    }
}
bool check(int x)//删去一条边后最大边是否<=mid 
{
    maxx=0,cnt2=0,tmp2=0;
    memset(cf,0,sizeof(cf));
    memset(a,0,sizeof(num));
    for(re int i=1;i<=m;++i)
    {
        if(val[i]>x)
        {
            cf[fr[i]]++;
            cf[to[i]]++;//边差分 
            cf[cc[i]]-=2;
            cnt2++;
            maxx=max(maxx,val[i]);//记录最大长度 
        }
    }
    guide=0;//guide表示最大公共边,guide=0表示没找到 
    dfs2(1,0);
    if(!guide) return false;
    if(maxx-guide>x) return false;
    else return true;
}
int erfen()
{
    int l=0,r=sums2;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(check(mid)) r=mid-1;
        else l=mid+1;
    }
    return l;
}
int main()
{
    n=read(),m=read();
    for(re int i=1;i<n;++i)
    {
        x=read(),y=read(),z=read();
        add(x,y,z);
        add(y,x,z);
        sums2+=z;
    }
    for(re int i=1;i<=m;++i) fr[i]=read(),to[i]=read();
    pre();
    dfs(1,0,0);
    for(re int i=1;i<=m;++i)
    {
        
        tmp=lca(fr[i],to[i]);
        cc[i]=tmp;//记录一下最近公共祖先，常数优化 
        val[i]=dis[fr[i]]+dis[to[i]]-dis[tmp]*2;//前缀和O(1)计算 
    }
    printf("%d\n",erfen());
    return 0;
} 

NOIP2015 运输计划

原文：https://www.cnblogs.com/Liuz8848/p/11676338.html