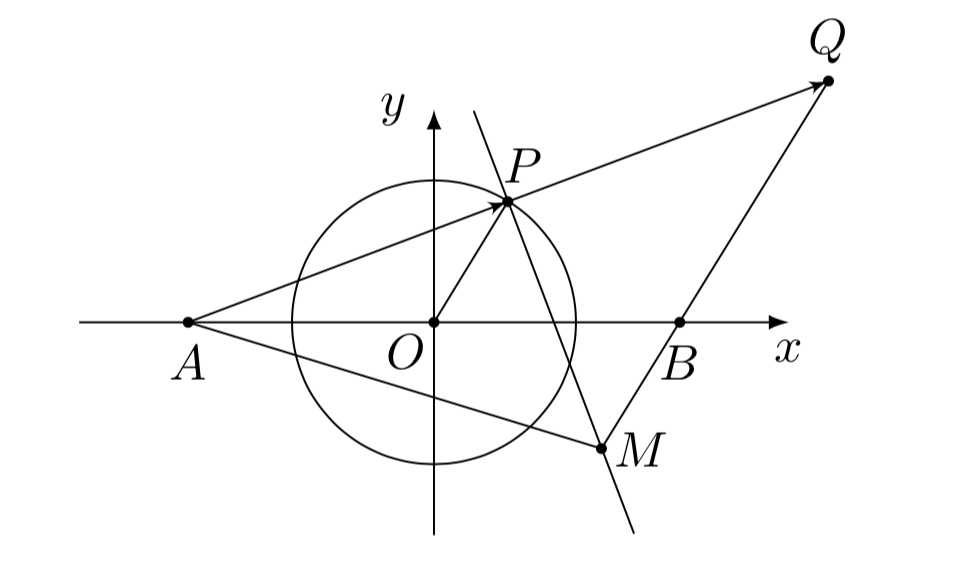
已知\(A(-\sqrt{3},0)\),\(B(\sqrt{3},0)\),\(P\)为圆\(x^2+y^2=1\)上的动点,\(\overrightarrow{AP}=\overrightarrow{PQ}\),过点\(P\)作与\(AP\)垂直的直线\(l\)交直线\(QB\)于点\(M\),则\(M\)的横坐标范围是\((\qquad)\)
\(\mathrm{A}. |x|\geqslant 1\) \(\qquad\mathrm{B}. |x|> 1\) \(\qquad \mathrm{C}.|x|\geqslant 2\) \(\qquad \mathrm{D}.|x|\geqslant \dfrac{\sqrt{2}}{2}\)
解析:
如图所示,容易知道
原文:https://www.cnblogs.com/Math521/p/11681870.html