上一节讲的是双曲抛物面,这节讲与之类似的椭圆抛物面.
抛物面是二次曲面的一种。抛物面有两种:椭圆抛物面和双曲抛物面。
椭圆抛物面在笛卡儿坐标系中的方程为:

双曲抛物面在笛卡儿坐标系中的方程为:

本文将展示几种生成椭圆抛物面算法和切图.使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815
(1)参数方程
#http://www.mathcurve.com/surfaces/alysseid/alysseid.shtml vertices = D1:100 D2:100 v = from 0 to (PI*2) D1 u = from 0 to 5 D2 a = 2.0 x = u*cos(v) y = 10 - pow(u, a) z = u*sin(v)
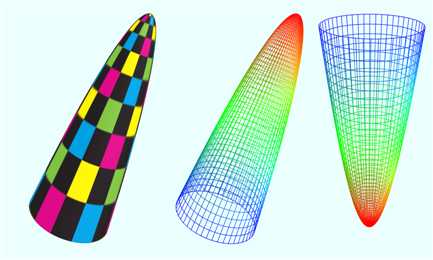
(2)普通方程
vertices = dimension1:101 dimension2:101 x = from (-100) to (100) dimension1 z = from (-100) to (100) dimension2 y = (20000 - x^2 - z^2)*0.005 u = x/10 v = z/10
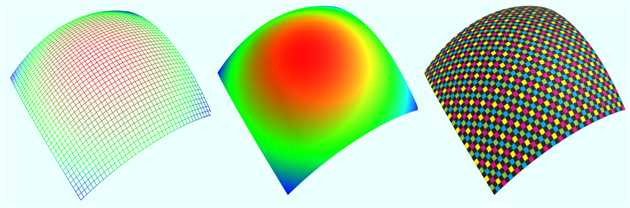
(3)椭圆
vertices = D1:100 D2:100 u = from 0 to (2*PI) D1 v = from 0 to 5 D2 a = rand2(1, 10) b = rand2(1, 10) x = v*a*cos(u) y = v*v/2 z = v*b*sin(u)
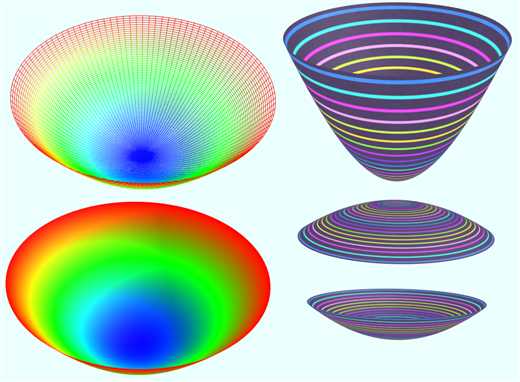
(4)将抛物线绕中轴旋转生成的椭圆抛物面
vertices = D1:512 D2:100 u = from 0 to 5 D1 v = from 0 to (2*PI) D2 a = rand2(-1, 1) x = u*cos(v) y = a*(u*u - 25) z = u*sin(v) v = v*2

原文:http://www.cnblogs.com/WhyEngine/p/3926350.html