从大一就开始搞算法,结果到现在对这些的理解都还这么浅。。。
dfs(深度优先搜索):这种算法最形象的描述就是不撞南墙不回头,不达到目的就一直往一个方向搜,实现算法使用的是递归,每到一个新的点就会有一些信息被更新,将这些更新后的信息作为参数传入下一层,如果一个方向的深搜出口不符合条件那么就回溯到上一个点,并且上一个点的信息仍然没有改变.,总结一下就是搜索深度优先,能深就不回去
bfs(广度优先搜索):就和dfs是反着的,利用队列来实现,bfs优先搜索广度,就是把一个点的能到的所有点先确定了后再向深度进行搜索。
我们拿一个图来说明
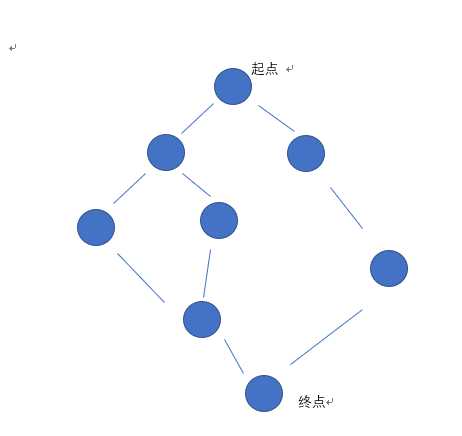
如果用dfs来走,那么就像这样
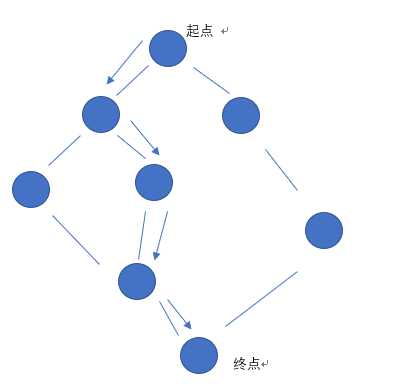
这就是用dfs搜索的一条路径,可以看出,如果走一条路要用1分钟的话,那么用dfs走到终点的路径不一定是时间最短的。
1 void dfs(当前点) 2 { 3 if(达到条件) //递归出口 4 return ; 5 通过某种方法从当前点到下一个点tmp; 6 dfs(tmp); 7 }
再看看bfs
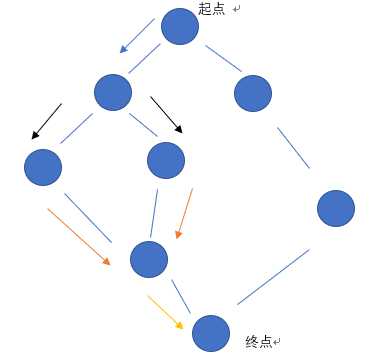
其中颜色相同的线表示他们所指目的地是同时检测的,当然我这里只画了左边的一半。这种情况下我们到达终点还是不能确保时间最短(但是如果利用优先队列就可以)。
void bfs(int start) { queue<int>q; q.push(start);vis[start]=1;//vis一般记录一下某个点有没有访问过,比如如果终点访问到了就结束,或者一个点访问了就不用访问 while(!q.empty()) { int s=q.front();q.pop(); 通过某种方式到下一个点next; if(!vis[next]) { q.push(next); } 如果到达终点就结束 } }
dfs和bfs我的理解还是不深,有时候不能搞清楚用哪个,因为有些时候两个用都可以,但有时候却只能用其中一个,或者其中一个简单,另一个十分复杂。
例题:poj3126,迷宫问题
dfs和bfs都可以找到起点到终点的路径,但只能找到存在性,如果有要求最优解那么就还要利用优先队列。
优先队列的bfs:顾名思义,就是在实现bfs的过程中用的是优先队列,优先队列可以对其中存储的结构的某些值进行自动的排序,依靠这个特点,在上面的例子中,我们可以拿结构体存每个点的信息(起点到这个点的时间和这个点的编号),存入优先队列时按照‘时间’从小到大,这样每次取出的第一个点到起点的时间都最短,如果这个点可以到终点,那么这个时间就是答案。
例题:poj2312 +代码
#include<iostream> #include<algorithm> #include<vector> #include<time.h> #include<cmath> #include<cstring> #include<cstdio> #include<cstdlib> #include<string> #include<functional> #include<map> #include<queue> #define mod (1000000000+7) #define maxn 2000+10 #define SIZE 400 #define lson rt<<1 #define rson rt<<1|1 #define midd (l+r)>>1 #define lowbit(x) (x&(-x)) typedef long long ll; const int inf_max = 0x3f3f3f3f; const int inf_min = 0xc0c0c0c0; const double eps=1e-5; using namespace std; string pr[2]={"No\n","Yes\n"}; int dir[][2]={1,0,-1,0,0,1,0,-1}; int n,m,vis[SIZE][SIZE]; char mp[SIZE][SIZE]; struct Point { int x,y,t; friend bool operator<(Point a,Point b) { return a.t>b.t; } friend bool operator== (Point a,Point b) { return (a.x==b.x)&&(a.y==b.y); } }start,fina; void BFS() { priority_queue<Point>q; vis[start.x][start.y]=1; q.push(start); while(!q.empty()) { Point next,now; now=q.top();q.pop(); for(int i=0;i<4;i++) { next.x=now.x+dir[i][0];next.y=now.y+dir[i][1]; if(next.x>=1&&next.x<=n&&next.y>=1&&next.y<=m&&!vis[next.x][next.y]&&mp[next.x][next.y]!=‘R‘&&mp[next.x][next.y]!=‘S‘) { int t1=1; if(mp[next.x][next.y]==‘B‘) t1++; vis[next.x][next.y]=1; next.t=now.t+t1; q.push(next); if(next==fina) { printf("%d\n",next.t); return ; } } } } printf("-1\n"); return ; } int main() { while(scanf("%d%d",&n,&m)&&(m+n)) { memset(vis,0,sizeof(vis)); memset(mp,0,sizeof(mp)); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { cin>>mp[i][j]; if(mp[i][j]==‘Y‘) { start.x=i; start.y=j; } if(mp[i][j]==‘T‘) { fina.x=i;fina.y=j; } } BFS(); } return 0; }
原文:https://www.cnblogs.com/codenameC6/p/11693676.html