题目要求:
给定一个数字,按照如下规则翻译成字符串:0翻译成“a”,1翻译成“b”...25翻译成“z”。一个数字有多种翻译可能,例如12258一共有5种,分别是bccfi,bwfi,bczi,mcfi,mzi。实现一个函数,用来计算一个数字有多少种不同的翻译方法。
解题思路:
下面我们从自上而下和自下而上两种角度分析这道题目,以12258为例:
自上而下,从最大的问题开始,递归 :
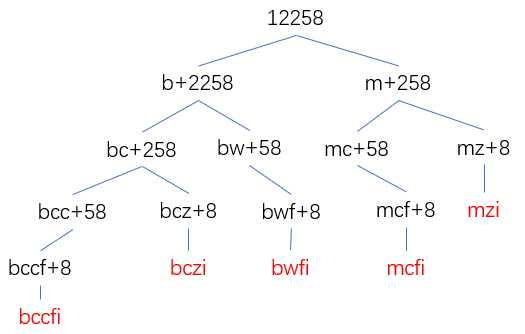
有很多子问题被多次计算,比如258被翻译成几种这个子问题就被计算了两次。
自然想到可以用动态规划来解决,用f(i)来表示从第i位数字开始不同的翻译数目,
我们可以写出转移矩阵
g(i,i+1)表示第i位和i+1位拼起来的数字在10~25范围内,值为1,否则为0。
先f(5) = 1, f(4) = 1
f(3) = f(4) + 0 = 1
f(2) = f(3) + f(4) = 2
f(1) = f(2) + f(3) = 3
f(0) = f(1) + f(2) = 5
1 1.动态规划 2 int Get_Translation(int num) 3 { 4 string str = to_string(num); 5 int digits = str.length(); 6 vector<int> dp(digits+1); 7 dp[0] = 1; 8 dp[1] = 1; 9 for(int i = 2; i < digits+1; ++i) 10 { 11 int temp = 10 * (str[i-2] - ‘0‘) + str[i-1] - ‘0‘;//计算十进制数 12 if (temp > 25) 13 dp[i] = dp[i - 1];//那么组不成新的子串 14 else 15 { 16 dp[i] = dp[i - 1] + dp[i - 2];//能组成新的串 17 } 18 } 19 return dp.back(); 20 } 21 2.递归 22 int getTransCount(const string & numstr, int i) 23 { 24 int len = numstr.size(); 25 //超过长度,只有一种可能 26 if (i >= len - 1) { 27 return 1; 28 } 29 //[i]和[i+1]可以组合成一个字符的,有两种方案 30 if (i + 1 < len ) { int sum = (numstr[i] - ‘0‘) * 10 + numstr[i + 1] - ‘0‘; if (sum > 9 && sum < 26) { 31 return getTransCount(numstr,i+1) + getTransCount(numstr,i+2); 32 } 33 } 34 //不能组合成一个字符的 35 return getTransCount(numstr, i + 1); 36 }
原文:https://www.cnblogs.com/zzw1024/p/11695535.html