单链表指的是线性表的每个结点,分散地存储在内存空间中,向后依次用一个指针串联起来。

其中:data称为数据域,next称为指针域/链域;当head==NULL时,为空表;否则为非空表,表为一个非空表时,在首结点,*head中会存放数据。

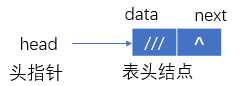
其中:head指向表头结点,head->data不放元素,head->next指向首结点a1,当head->next==NULL时,为空表。
1 1 struct node 2 2 { 3 3 ElemType data; //data为抽象元素类型 4 4 struct node *next; //next为指针类型 5 5 }; 6 //指向结点的指针变量head、p、q说明 7 struct node *head, *p, *q;
例1:输入一列整数,以0为结束标志,生成“先进先出”单链表“

这个单链表之所以称为先进先出单链表就是因为先进来的元素;通过变化表头指针可以先被删除。
首先定义结点空间所占大小,结点的数据域为整型数,然后定义指针域next。
1 #define LENG sizeof(struct node) //结点所占单元数 2 struct node //定义结点类型 3 { 4 int data; 5 struct node *next; 6 };
每次输入元素后:
1 struct node *creat1() 2 { 3 struct node *head, *tail, *p; 4 int e; 5 head=(struct node *)malloc(LENG); //生成表头结点 6 tail=head; //尾指针指向表头 7 scanf("%d", &e); //输入第一个数 8 while(e!=0); //不为0 9 { 10 p=(struct node *)malloc(LENG); //生成新结点 11 p->data=e; //装入输入的元素e 12 tail->next=p; //新结点链接到表尾 13 tail=p; //尾指针指向新结点 14 scanf("%d", &e); //再输入一个数 15 } 16 tail->next=NULL; //尾结点的next置为空指针 17 return head; //返回头指针 18 }

每次插入新元素后:
1 struct node *creat2() 2 { 3 struct node *head, *p; 4 head=(struct node *)malloc(LENG); //生成表头结点 5 head->next=NULL; //置为空表 6 scanf("%d", &e); //输入第一个数 7 while(e!=0); //不为0 8 { 9 p=(struct node *)malloc(LENG); //生成新结点 10 p->data=e; //输入数送新结点的data 11 p->next=head->next; //新结点指向原首结点 12 head->next=p; //表头结点的指针指向新结点 13 scanf("%d", &e); //再输入一个数 14 } 15 return data; //返回头指针 16 }
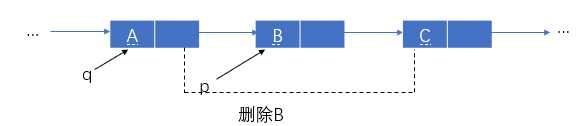
例1:在已知 p 指针指向的结点后插入一个元素x
首先用一个指针 f 指向新结点,该结点中的数据域为 x ,然后此新结点next域赋值为 p 指针指向结点的next域,最后 p 指针指向结点的next域赋值为 f 。
1 f=(struct node *)malloc(LENG); //生成 2 f->data=x; //装入元素x 3 f->next=p->next; //新结点指向p的后继 4 f->next=f; //新结点成为p的后继
例2:在已知 p 指针指向的结点前插入以一个元素x
因为单链表每个结点只有一个指针指向其后继结点,如果在结点前插入一个新结点,就需要得到指向 p 结点前驱结点的指针。
1 f=(struct node *)malloc(LENG); 2 f->data=x; 3 f->next=p; //新结点成为p的前驱 4 q->next=f; //新结点成为p的前驱结束的后继
例:输入一列整数,以0为结束标志,生成递增有序单链表。


可以分为以下几种情况:
p、q可能为NULL
注意一点每次扫描已经存在的单链表确定数据插入的位置之前,做如下的初始化:
1 q=NULL; 2 p=Head;
1 struct node *creat3_1(struct node *head, int e) 2 { 3 q=NULL; 4 p=head; //p、q扫描,查找插入位置 5 while(p&&e>p->data) //未扫描完,且e大于当前结点 6 { 7 q=p; 8 p=p->next; 9 } 10 f=(struct node *)malloc(LENG); //生成新结点 11 f->data=e; 装入元素e 12 if(p==NULL) 13 { 14 f->next=NULL; 15 if(q==NULL) //对空表的插入 16 head=f; 17 else 18 q->next=f; 19 } //作为最后一个结点插入 20 else if(q==NULL) //作为第一个结点插入 21 { 22 f->next=p; 23 q->next=f; //一般情况插入新结点 24 } 25 return head; 26 }
主函数算法
1 main() 2 { 3 struct node *head; //定义头指针 4 head=NULL; //置为空表 5 scanf("%d", &e); //输入整数 6 while(e!=0) //不为0,未结束 7 { 8 head=creat3_1(head, e) //插入递增有序单链表 9 scanf("%d", &e); 10 } 11 }
1 void creat3_2(struct node *head, int e) 2 { 3 q=head; 4 p=head->next; //p、q扫描,查找插入位置 5 while(p&&e->p->data) //未扫描完,且e大于当前结点 6 { 7 q=p; 8 p=p->next; //q、p后移,查下一个位置 9 } 10 f=(struct node *)malloc(LENG); //生成新结点 11 f->data=e; //装入新元素e 12 f->next=p; 13 q->next=f; //插入新结点 14 }
主函数算法
main() { struct node *head; //定义头指针 head=NULL; //置为空表 scanf("%d", &e); //输入整数 while(e!=0) //不为0,未结束 { head=creat3_2(head, e) //插入递增有序单链表 scanf("%d", &e); } }
输入:头指针L、位置i、数据元素e
输出:成功返回OK,失败返回ERROR
计数如果在第 i 个位置上结束,p 指向第 i 个位置,新元素就要插入到 p 指向的结点之前,我们之前分析过,如果插入到某个结点之前,就需要另一个复制指针 q 来指向 p 的前驱结点。

执行:p=L
当 p 不为空,执行 p=p->next i-1次
定位到第 i-1 个结点
当 i<1 或 p 为空时插入点错
否则新结点加到 p 指向结点之后
1 int insert(Linklist &L, int i, ElemType e) 2 { 3 p=L; 4 j=1; 5 while(p&&j<i) 6 { 7 p=p->next; //p后移,指向下一个位置 8 j++; 9 } 10 if(i<1||p==NULL) //插入点错误 11 return ERROR; 12 f=(Linklist)malloc(LENG); //生成新结点 13 f->data=e; //装入元素e 14 f->next=p->next; 15 p->next=f; //插入新结点 16 return OK; 17 }
主要是三个大的部分:
1 int Delete1(Linklist head, ElemType e) 2 { 3 struct node *q, *p; 4 q=head; 5 p=head->next; //q、p扫描 6 while(p&&p->data!=e) //查找元素为e的结点 7 { 8 q=p; //记住前一个结点 9 p=p->next; 查找下一个结点 10 } 11 if(p) //有元素为e的结点 12 { 13 q->next=p->next; //删除该结点 14 free(p); //释放结点所占的空间 15 return YES; 16 } 17 else 18 return NO; //没有删除结点 19 }

执行:p=L;
当 p 不为空,执行p=p->next i-1次,定位到第 i-1 个结点
当 i<1 时或p->next为空时删除点错,否则 p 指向后继结点的后继跳过原后继
1 int Delete2(Linklist &L, int i, ElemType &e) 2 { 3 p=L; 4 j=1; 5 while(p->next&&j<i) //循环结束时p不可能为空 6 { 7 p=p->next; //p后移,指向下一个位置 8 j++; 9 } 10 if(i<1||p->next==NULL) //删除点错误 11 return ERROR; 12 q=p->next; //q指向删除结点 13 p->next=q->next; //从链表中指出 14 e=q->data; //取走数据元素值 15 free(p); //释放结点空间 16 return OK; 17 }
两个有序单链表的合并算法
将两个有序单链表La和Lb合并为有序单链表Lc;(该算法利用原单链表的结点)
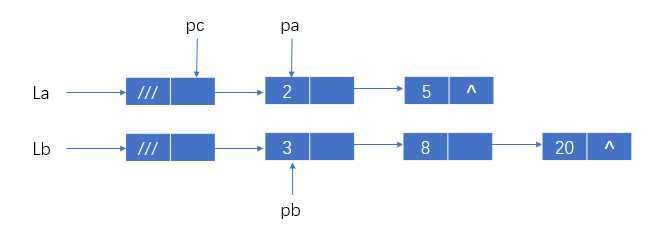
输入:两单链表的头指针
输出:合并后的单链表的头指针
1 struct node *merge(struct node *La, struct node *Lb) 2 { 3 struct node *pa, *pb, *pc; 4 pa=La->next; //pa指向表La的首结点 5 pb=Lb->next; //pb指向表Lb的首结点 6 pc=La; //使用表La的头结点,pc为尾指针 7 free(Lb); //释放表Lb的头结点 8 //比较pa指向pb指向结点的数据域值大小 9 while(pa&&pb) //表La表Lb均有结点 10 if(pa->data<=pb->data) //取表La的一个结点 11 { 12 pc->next=pa; //插在表Lc的尾结点之后 13 pc=pa; //变为表Lc新的尾结点 14 pa=pa->next; //移向表La下一个结点 15 } 16 else //取表Lb的一个结点 17 { 18 pc->next=pb; //插在表Lc的尾结点之后 19 pc=pb; 20 pb=pb->next; 21 } 22 if(pa) 23 pc-next=pa; //插入表La的剩余段 24 else 25 pc->next=pb; //插入表Lb的剩余段 26 return La; 27 }
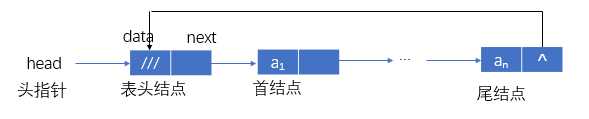
有:H->next≠H,H≠NULL。
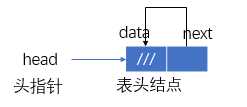
有:H->next≠H,H≠NULL。

有:tail指向表尾结点
tail->data=an
tail->next 指向表头结点
tail->next->next 指向首结点
tail->next->next->data=a1
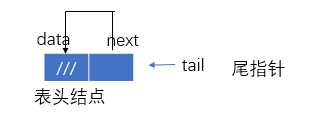
有:tail->next=tail
如果是带头指针,时间复杂度 O(m+n)
如果使用只设尾指针的循环链表
1 p2=tail2->next; 2 tail->next=tail->next; 3 tail1->next=p2->next; 4 free(p2);
时间复杂度 O(1)
例:求以head为头指针的循环单链表的长度,并依次输出结点的值。
1 int length(struct node *head) 2 { 3 int leng=0; //长度变量初值为0 4 struct node *p; 5 p=head->next; //p指向首结点 6 while(p!=head) //p未移回到表头结点 7 { 8 printf("%d", p->data); //输出 9 leng++; //计数 10 p=p->next; //p移向下一个结点 11 } 12 return leng; 13 }

1 //结点类型定义 2 struct Dnode 3 { 4 ElemType data; //data为抽象元素类型 5 struct Dnode *prior, *next; //prior,next为指针类型 6 }; 7 //或者 8 typedef struct Dnode 9 { 10 ElemType data; 11 struct Dnode *prior, *next; 12 } *DList

有:L为头指针,L指向表头结点,L->next指向首结点
L->next->data=a1
L->prior指向尾结点,L->prior->data=an
L->next->prior=L->prior->next=NULL

有:L->next=L->prior=NULL
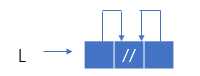
有:L->next=L->prior=L

设 p 指向 a1,有:
p->next 指向 a2 ,p->next->prior 指向 a1
所以,p=p->next->prior
同理,p=p->prior->next
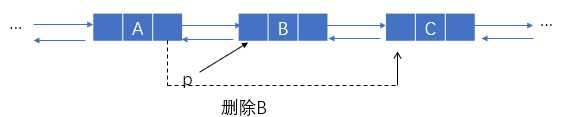
1 //执行 2 p->prior->next=p->next; //结点A的next指向结点C 3 p->next->prior=p->prior; //结点C的prior指向结点A 4 free(p); //释放结点B占有的空间
1 f->prior=p->prior; //结点B的prior指向结点A 2 f->next=p; //结点B的next指向结点C 3 p->prior->next=f; //结点A的next指向结点B 4 p->prior=f; //结点C的prior指向结点B
原文:https://www.cnblogs.com/tronysh/p/11695484.html