问题描述

题目描述
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树.
假设输入的前序遍历和中序遍历的结果中都不含重复的数字
例:
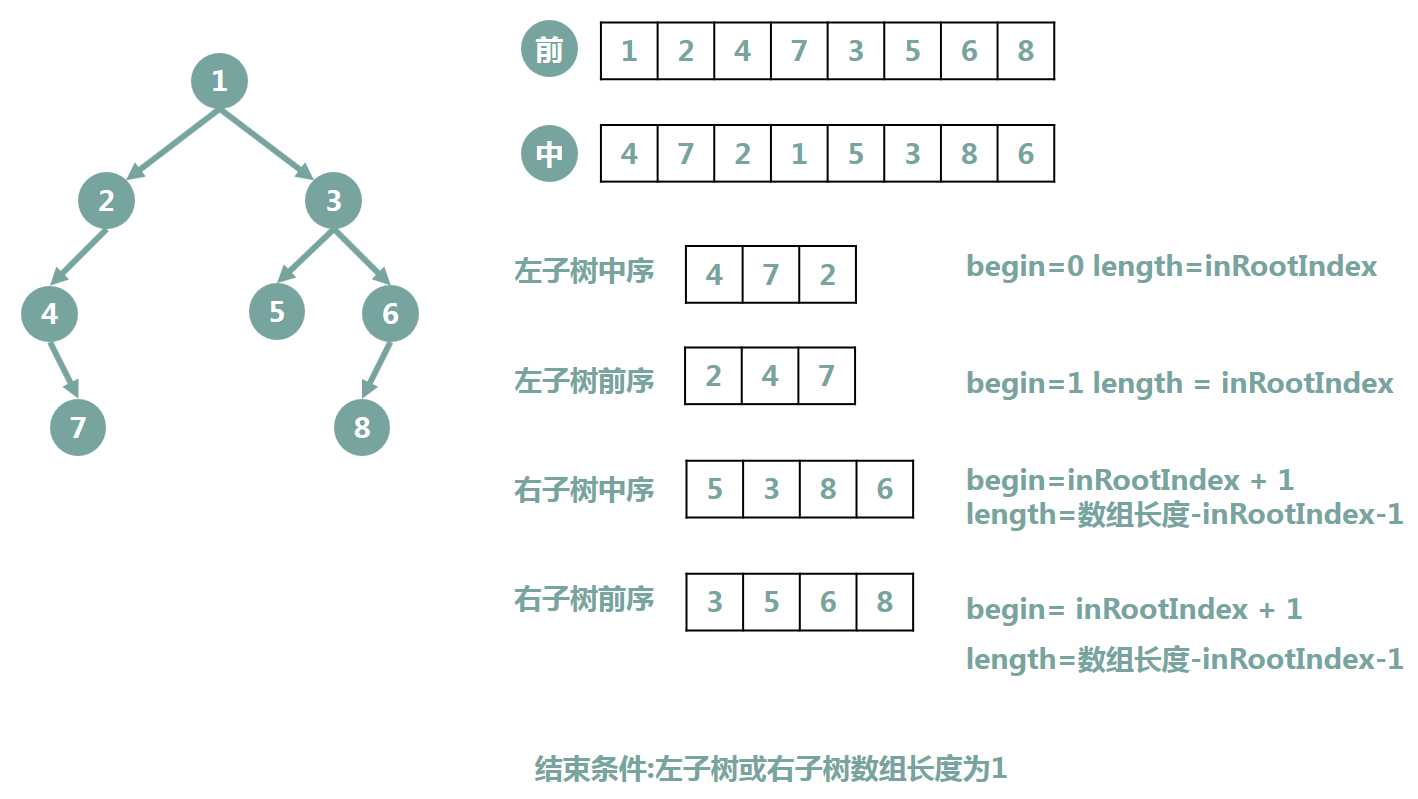
前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
方法原型

public TreeNode reConstructBinaryTree(int [] pre,int [] in)
class TreeNode {
      int val;
      TreeNode left;
      TreeNode right;
      TreeNode(int x) { val = x; }
}

解题思路

手工还原

虽然本题是一道编程题，但是也经常以填空题的方式考察，比如问：
已知某树的：

• 前序遍历序列为{1,2,4,7,3,5,6,8}
• 中序遍历序列为{4,7,2,1,5,3,8,6}

求该树的后序遍历。解决这个问题的原则有两个，第一个是根出现在前序遍历最开始；其次是中序遍历中左、右子树元素出现在根的左右两边。
以上题为例，首先看前序遍历，我们知道树的根节点为1，然后去看中序遍历，发现1的左边有4,7,2；右边有5,3,8,6。可以知道根节点的左子树有4，7，2；而右子树有5，3，8，6.

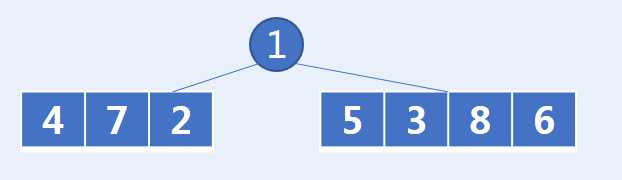
那么接着如何去确认左子树的形状呢？方法与刚才一样：先在前序遍历中确认根节点；然后在中序遍历中确认左、右子树。
以4, 7, 2序列为例，在前序遍历中可以查看到2最先出现，因此2是这个子树的根节点，然后在中序遍历中，发现4、7都在2的左边，因此2的左子树有4、7，右子树为空，结构如下：

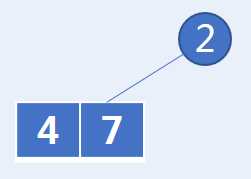
然后，对于4、7子树，可以在前序遍历中得知4是根节点，7是4的右孩子。

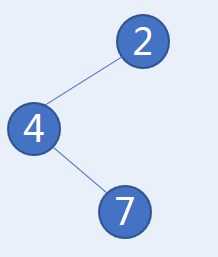
反复使用以上规则，可以还原整个树的结构，以下是完整的动图演示：

我们就通过以上还原的过程，得到了树的原有形状为：

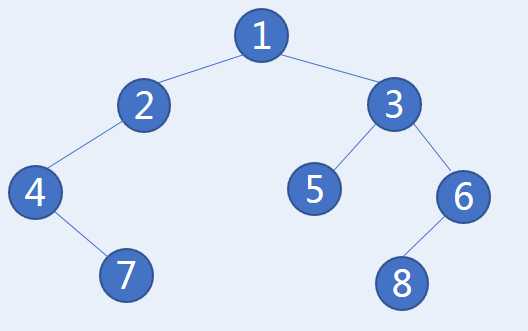
自然可以知道其后序遍历为{7,4,2,5,8,6,3,1}。

编程还原

学会手工还原树后，我们将写代码实现树的重构，其思路如之前所总结：

• 通过前序遍历确认根节点
• 通过中序遍历确认左、右子树
• 以上过程递归，知道还原到叶子节点

在具体的代码实现过程中，我们除了使用递归算法外，还使用一个inRootIndex变量用于区分左、右子树。

相关代码

package com.shellmad;

public class Solution {

    public static void main(String[] args) {
        int[] pre = {1,2,4,7,3,5,6,8};
        int[] in = {4,7,2,1,5,3,8,6};
        Solution solution = new Solution();
        TreeNode root = solution.reConstructBinaryTree(pre, in);
        System.out.println(root);
    }

    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        // 检查输入
        if (pre == null || in == null || pre.length == 0 || in.length == 0
            || pre.length != in.length) {
            return null;
        }

        // 判断是否是叶子节点
        if (pre.length == 1) {
            return new TreeNode(pre[0]);
        }

        // 在中序遍历中找到根节点的位置
        int rootIndex = -1;
        for (int index = 0; index < in.length; index++) {
            if (pre[0] == in[index]) {
                rootIndex = index;
                break;
            }
        }

        if (rootIndex == -1) {
            return null;
        }

        // 创建根节点
        TreeNode root = new TreeNode(pre[0]);

        // 递归构建左子树
        if (rootIndex != 0) {
            int lSubTreeLegth = rootIndex;
            int[] leftPre = new int[lSubTreeLegth];
            int[] leftIn = new int[lSubTreeLegth];

            for (int index = 0; index < lSubTreeLegth; index++) {
                leftPre[index] = pre[1 + index];
                leftIn[index] = in[index];
            }

            root.left = reConstructBinaryTree(leftPre, leftIn);
        }

        // 递归构建右子树
        if (rootIndex != in.length - 1) {
            int rSubTreeLegth = in.length - 1 - rootIndex;
            int[] rightPre = new int[rSubTreeLegth];
            int[] rightIn = new int[rSubTreeLegth];

            for (int index = 0; index < rSubTreeLegth; index++) {
                rightPre[index] = pre[rootIndex + 1 + index];
                rightIn[index] = in[rootIndex + 1 + index];
            }

            root.right = reConstructBinaryTree(rightPre, rightIn);
        }
        return root;
    }
}




class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

经典算法题-基础-重构二叉树

原文：https://www.cnblogs.com/shellmad/p/11706164.html