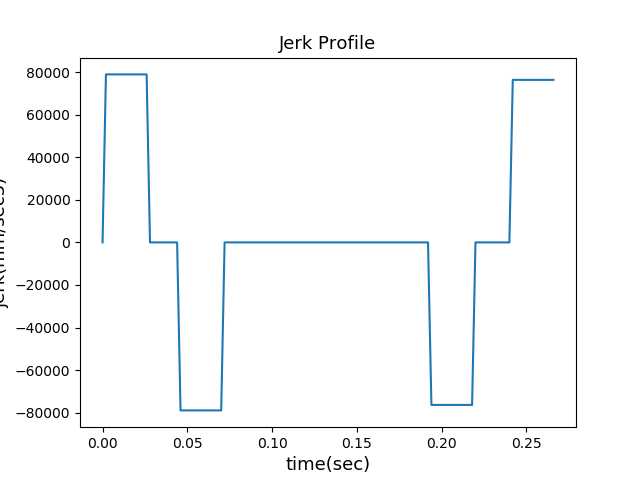
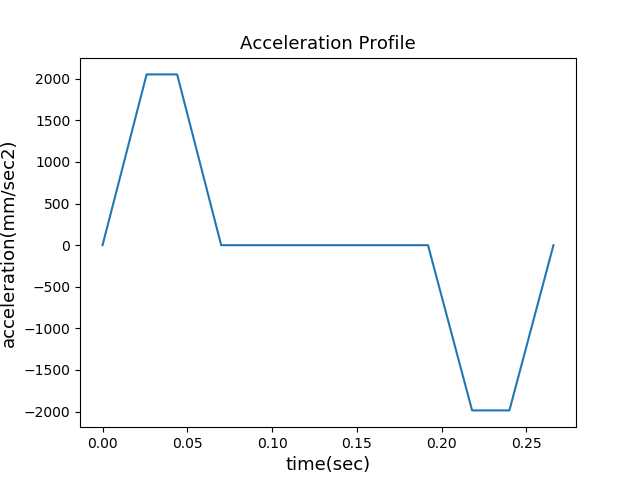
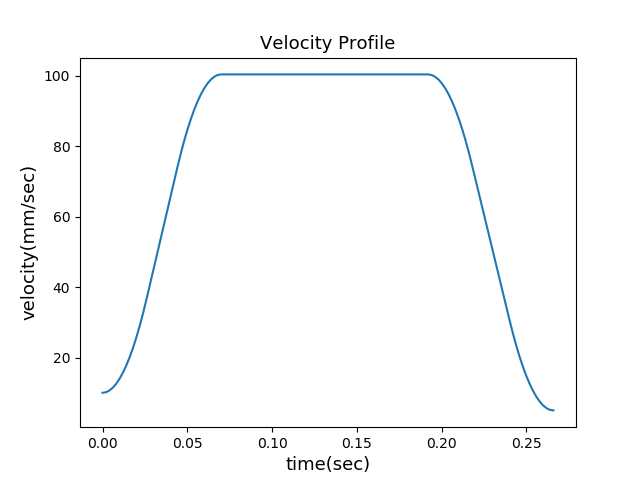
3rd S-curve
 (1)
(1)
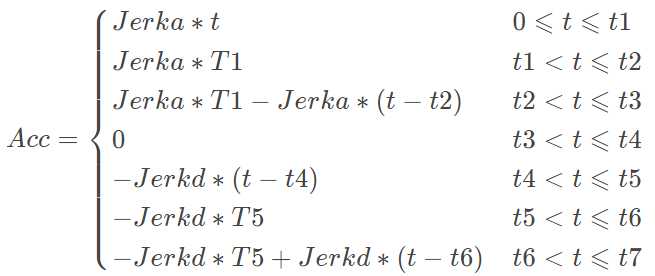 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
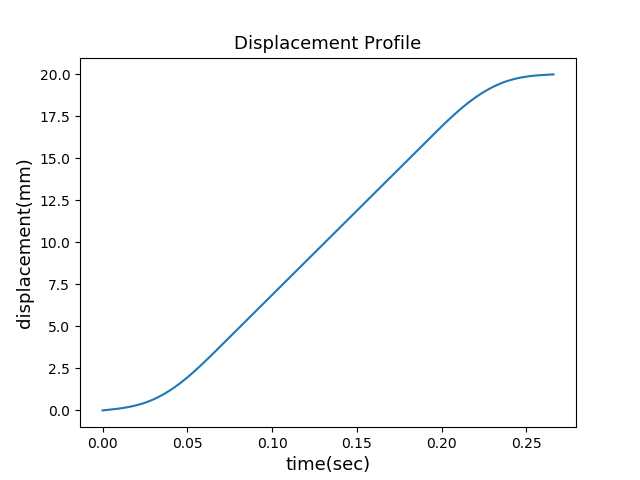
完整的三次S曲线包括上面的七个阶段。前面三个阶段为加速阶段,从初始速度Vs加速到Vmax:
![]() (5)
(5)
整个加速阶段的位移为:
![]() (6)
(6)
后面三个阶段为减速阶段:
![]() (7)
(7)
![]() (8)
(8)
也可以看作为反向加速阶段,即速度从最终速度Ve加速到Vmax:
![]() (9)
(9)
![]() (10)
(10)
中间的阶段为匀速阶段:
![]()
![]() (11)
(11)
但是在实际中,受限于Vs,Ve,以及位移L,整条速度曲线并不包含完整的七个阶段,通常Jerka = Jerkd = Jerk。那么求速度曲线可以转换为以下数学问题:已知Vs,Ve,L,Amax,Jerk,Fmax,求解下面的四元三次方程组:
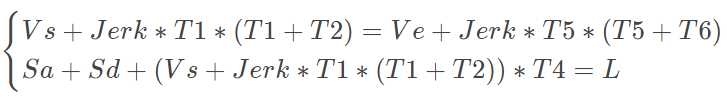 (12)
(12)
其中,Sa和Sd分别由式(6)和(10)计算,并且需要满足以下限制条件:
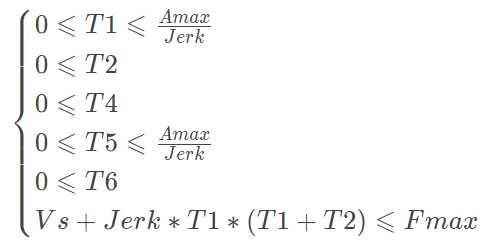 (13)
(13)
这是一个非齐次的非线性的方程组。四个未知数,但是只有两个方程以及一些限制条件。给定初值然后利用迭代法计算也许是求解的一种途径。在设定初值上,可以分情况进行讨论。流程图如下图所示。
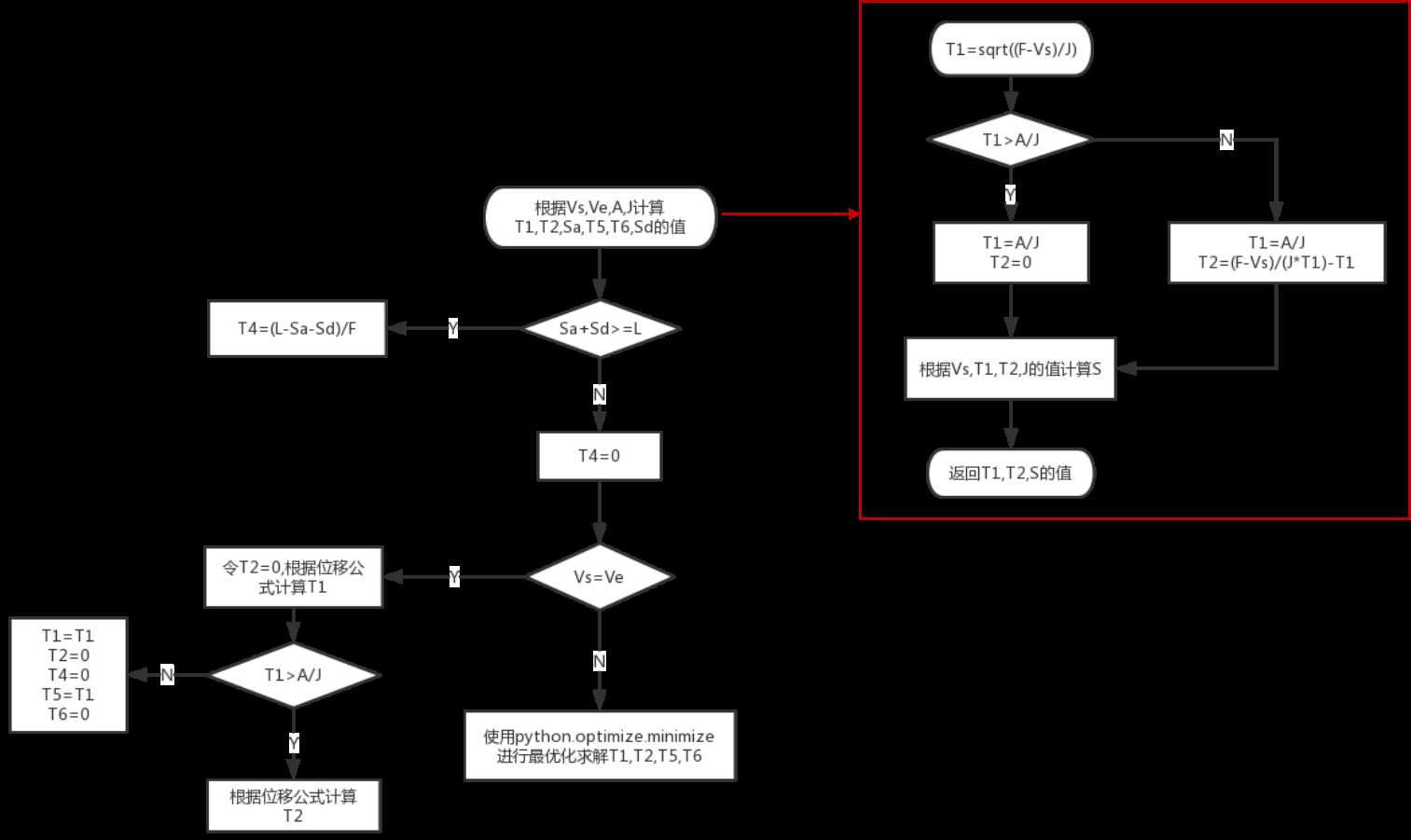
首先使用Vs,Ve,Fmax,Amax,Jerk的值计算T1,T2,T5,T6。计算过程中先假设T2=0,计算速度从Vs达到Fmax所需的时间T1,如果T1<Amax/Jerk,则没有上面的第二个阶段,即加速度匀速的阶段。如果T1>Amax/Jerk,则T1会受到最大加速度的限制,即T1=Amax/Jerk,T2=(Fmax-Vs)/(Jerk*T1)-T1,并且根据T1,T2通过式(6)可以计算出加速阶段的位移Sa。同理可以计算出T5,T6和Sd。
如果Sa+Sd>=L,则说明最大速度可以保持匀速一段时间T4,T4=(L-Sa-Sd)/Fmax
如果Sa+Sd<L,则说明T4=0,且整条速度曲线的峰值达不到最大速度Fmax。因此问题转换为如下的数学问题:
![]() (14)
(14)
求T1,T2,T5,T6。
当Vs=Ve时,T1=T5,T2=T6,则求解式(14)就变成求解式(15)的解:
![]() (15)
(15)
也是先假设T2=0,则式(15)是一个关于未知数T1的一元三次方程,且因其判别式大于零,其有唯一解。因此可以求得T1。若T1<Amax/Jerk,则T2=0,若T1>Amax/Jerk,则T1=Amax/Jerk,然后再通过式(15)计算T2。
当Vs≠Ve时,方程组有四个未知数,求不到其唯一解。因此本文中采用的是Python.scipy库中的求最小值的问题来计算T1,T2,T5,T6。即解决如下数学问题:
求T=[T1,T2,T5,T6],使得
![]() (16)
(16)
值最小,其中,Vmax=Vs+J*T1*(T1+T2)。并满足如下的条件:
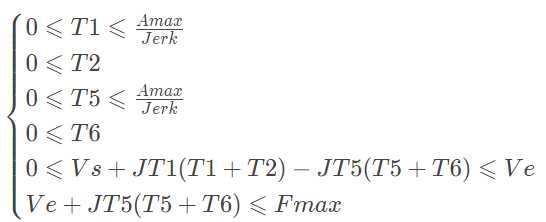 (17)
(17)
下面为这段python代码:
import numpy as np from scipy.optimize import minimize import math def motion_profile(args): vs,J,Fmax,L,t = args s=lambda x: (vs*t*(2*x[0]+x[1])+J*x[0]*math.pow(t,3)*(2*x[0]+x[1])*(x[0]+x[1])+(vs+J*x[0]*math.pow(t,2)*(x[0]+x[1]))*(2*x[2]+x[3])*t-J*x[2]*math.pow(t,3)*(2*x[2]+x[3])*(x[2]+x[3])-L)**2 return s def cons(args): Fmax,ve,Amax,J,vs,t = args cons = ({‘type‘:‘ineq‘, ‘fun‘:lambda x:np.array([Amax/J - x[0]*t, x[0], x[1], x[2], x[3], Amax/J - x[2]*t, ve-vs-J*(x[0]*t)**2 -J*x[0]*t*x[1]*t + J*x[2]*t*x[3]*t + J*(x[2]*t)**2, Fmax-ve-J*x[2]*math.pow(t,2)*(x[2]+x[3]), vs + J*(x[0]*t)**2 + J*x[0]*t*x[1]*t - J*x[2]*t*x[3]*t -J*(x[2]*t)**2])}) return cons def optimization(args,args1,x0): conditions = cons(args1) res = minimize(motion_profile(args),x0,method=‘SLSQP‘,constraints = conditions) time_list = [] time_list.append(res.x[0]) time_list.append(res.x[1]) time_list.append(res.x[2]) time_list.append(res.x[3]) return time_list
整个代码可以见github:
https://github.com/Larissa1990/S-curve-Velocity-Profile
Example1:
Vs=40,Ve=35,Fmax=80,Amax=2000,Jerk=80000,L=5,interpolation_period=0.002
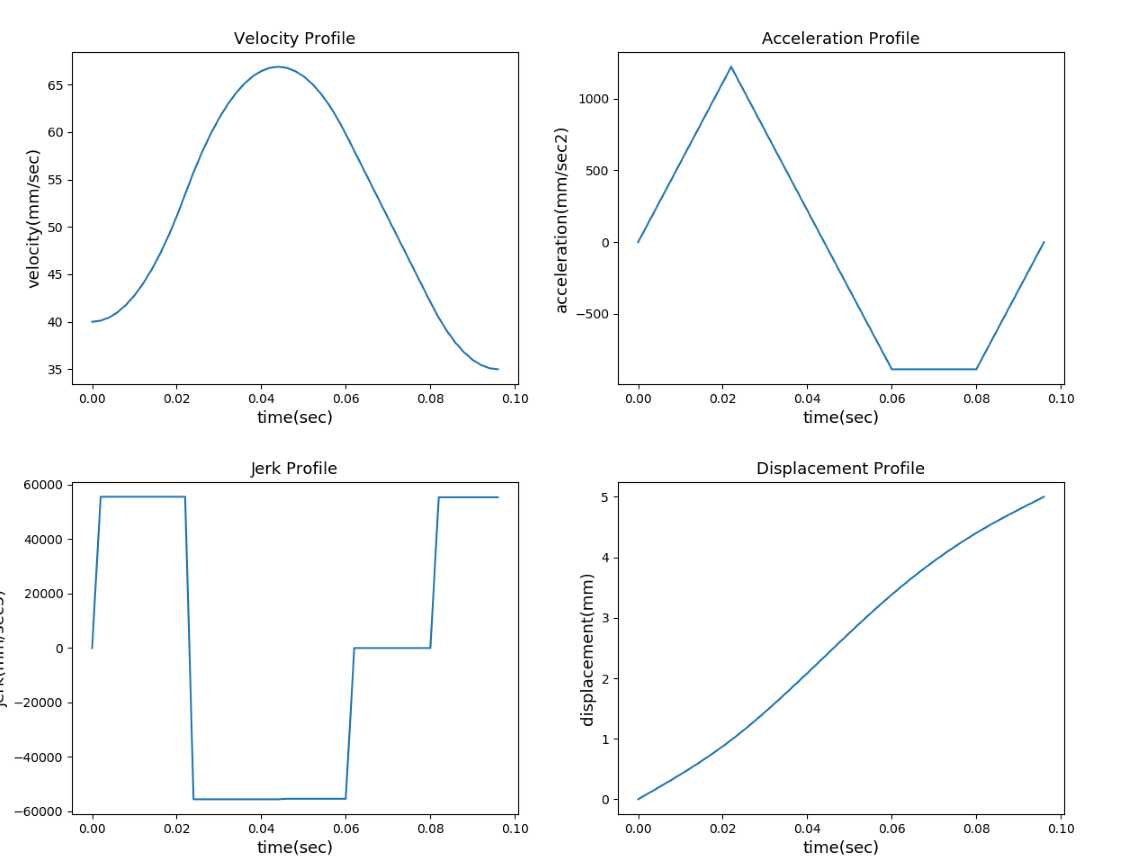
T1=0.022,T2=0,T4=0,T5=0.016,T6=0.02
Example2:
Vs=35,Ve=35,Fmax=80,Amax=2000,Jerk=80000,L=5,interpolation_period=0.002
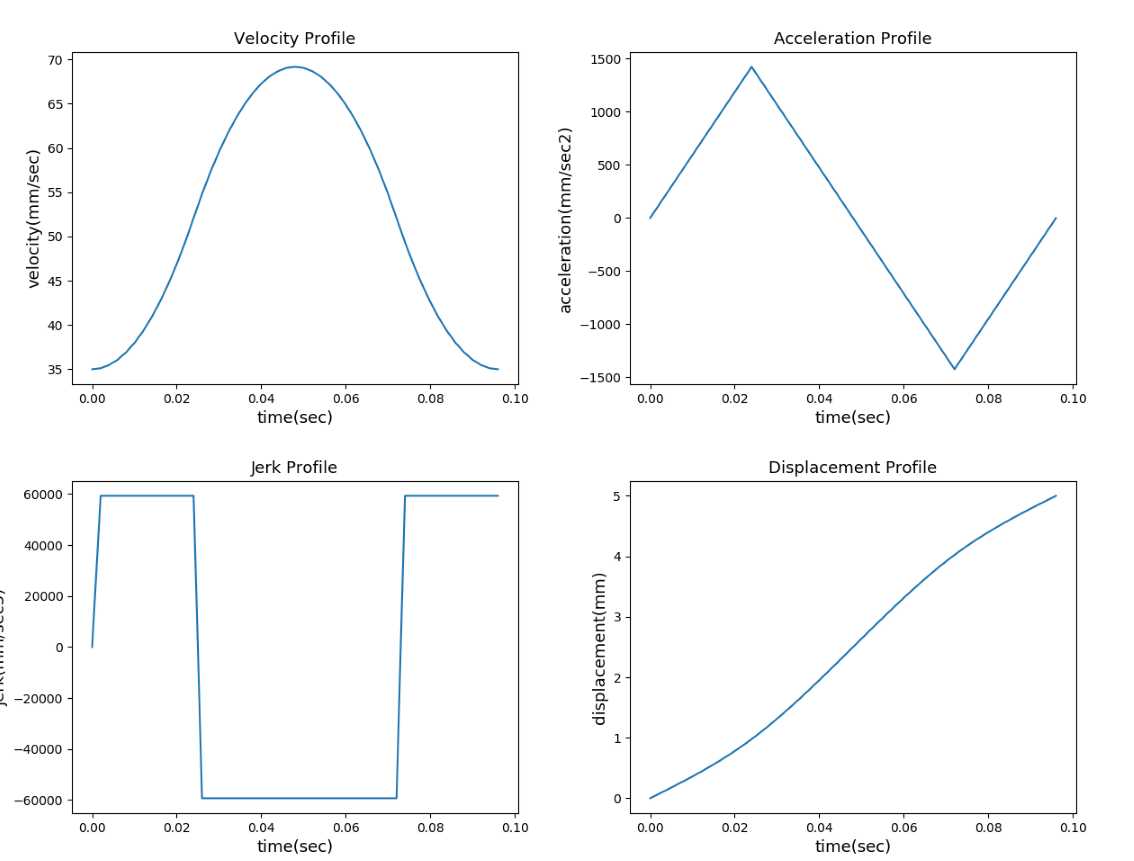
T1=0.024,T2=0,T4=0,T5=0.024,T6=0
原文:https://www.cnblogs.com/larissa-0464/p/11628859.html