线性表
应用:多项式的表示
什么是线性表
多项式表示问题给出的启示:
同一个问题可以有不同的表示(存储)方法
有一类共性问题 : 有序线性序列的租住和管理
“线性表(Linear List)” : 由同类型数据元素构成有序序列的线性结构
表中元素个数称为线性表的长度
线性表没有元素时,称为空表
表起始位置称为表头,表结束位置称为表尾
线性表的抽象数据类型描述
类型名称 : 线性表(List)
数据对象集: 线性表是 n(>=0) 个元素构成的有序序列(a_1, a_2, a_3, ...., a_n)
操作集: 线性表L属于List, 整数i表示位置, 元素X属于ElementType
线性表基本操作主要有:
List MakeEmpty(): 初始化一个空性表L;
ElementType FindKth(int K, List L): 根据位序K, 返回相应元素;
int Find(ElementType X, List L) : 在线性表L中查找X的第一次出现位置;
void Insert(ElementType X, int i, List L): 在位序i前插入一个新元素X;
void Delete(int i, List L) : 删除指定位序i的元素;
int Length(List L) : 返回线性表L的长度n;
线性表的顺序存储实现
利用数组的连续存储空间顺序存放线性表的各元素

#define MAXSIZE <............>
typedef struct LNode *List;
struct LNode{
ElementType Data[MAXSIZE];
int Last;
};
struct LNode L;
List PtrL;
访问下标为i的元素:L.Data[i] 或 PtrL->Data[i]
线性表的长度: L.Last+1 或PtrL->Last+1
主要操作的实现
List MakeEmpty()
{
List PtrL;
PtrL = ( List )malloc( sizeof( struct LNode ) );
PtrL->Last = -1;
return PtrL;
}
查找
int Find(ElementType K, List PtrL)
{
int i = 0;
while ( i <= PtrL->Last && PtrL->Data[i] != X)
i++;
if ( i > PtrL->Last) return -1; //如果没有找到, 返回-1
else return i;//找到后返回的是存储位置
}
插入(第 i (1 <= i <= n+1)个位置上插入一个值为X的新元素)
这里的要注意的是, 这里的代码是采用的从1开始计数的设计
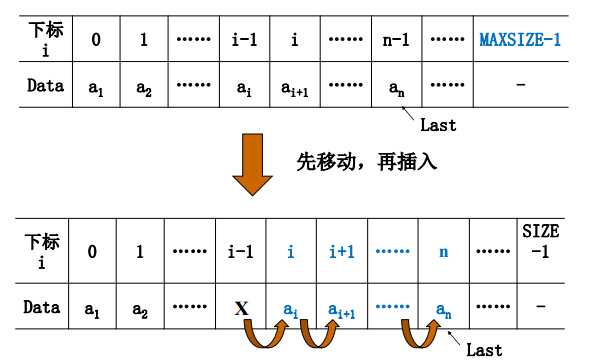
插入操作的具体实现
需要注意这里的是, 这里的位置是从1开始计数(就是人类默认的第一位置的元素就是第一个,对于计算机中来说,还可以有从0开始计数,普遍的来说,在计算机中大都是从0开始计数的)
void Insert ( ElementType X, int i, List PtrL)
{
int j;
if ( PtrL->Last == MAXSIZE - 1){ //表的空间已满, 不能插入新的元素(这里的MAXSiZE - 1是能插入进去的最后的一个位置, 而MASIZE代表的是表中元素最多的元素个数)
printf ( " 表满 ");
return ;
}
if ( i < 1 || i > PtrL->Last+2){
/*对于 PtrL->Last 表示的数链表中数组元素的最后一个元素的位置信息(这里的位置信息时采用从0开始计数的),因此要是采用从1开始计数的话,这个位置就是第PtrL->Last + 1 位置上的元素, 但是要插入元素的范围是在(1 <= i <= n+1) 即, 第一位置开始, 到第n + 1位置开始, 因此这里的最后一个位置要插入的位置(第n+1位置)用PtrL->Last表示的话就是PtrL->Last + 2位置,
所以这里判断的i 的范围,就可以很容易的知道这里的范围的含义。*/
printf ( " 位置不合法 ");
return;
}
for ( j = PtrL->Last; i >= i - 1; j--)
PtrL->Data[j + 1] = PtrL->Data[j];//将a_i .... a_n 倒序向后移动
PtrL->Data[i - 1] = X;//新元素插入
PtrL->Last++;//Last仍指向最后元素
return;
}
//插入的另一个版本, 这里采用的计数就是在0开始进行计数的
void Insert(List L, Elementype X, Position P)
{
/*在L的指定位置P前插入一个新元素X*/
Position i;
if(L->Last == MAXSIZE -1)
{
/*表空间已满,不能插入*/
printf("表满");
return FALSE;
}
if( P < 0 || P > L->Last + 1){//这里是变化的不同之处,这里的采用的就是从0开始计数判断插入位置的合法性
//检查插入位置时候合法
printf("位置不合法");
return FALSE;
}
for( i = L->Last; i >= P; i--)
L->Data[i+1] = L->Data[i]; //将位置P以及以后位置往后移动
L->Data[P] = X;//新元素插入
L->Last++;//Last 仍指向最后一个元素
return ;
}
删除(删除表的第 i (1 <= i <=n)个位置上的元素)
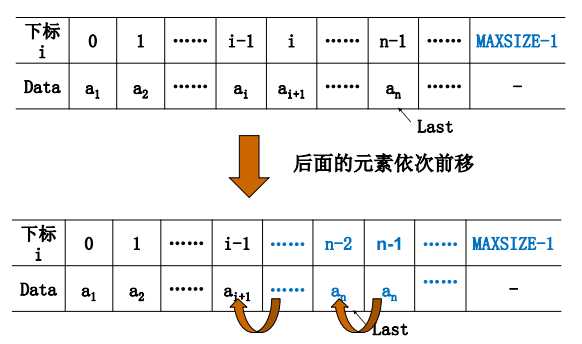
删除操作的实现 (这里也是有位置计数的为题,下面这个采用的是从第1个位置开始计数的)
void Delete( int i, List PtrL)
{
int j;
if ( i < 1 || i > PtrL->Last + 1){
printf ( "不存在第%d个元素", i);
return;
}
for ( j = i; j <= PtrL->Last; j++)
PtrL->Data[j - 1] = PtrL->Data[j];//将a_(i+1) ..... a_n顺序向前移动
PtrL->Last--;//Last仍指向最后元素
return ;
}
//这里采用的计数位置是从0开始计数的
BOOL Delete(List L, Position P)
{
//从L 中删除指定位置P的元素
Position i;
if ( P < 0 || P > L->Last){
//检查空表集删除位置的合法性
printf("位置%d不存在元素",P);
return FALSE;
}
for( i = P + 1; i <= L->Last; i++)
L->Data[i - 1] = L->Data[i];//将位置P+1及以后的位置往前移
L->Last--;//last 指向最后一个元素
return TRUE;
}
完整测试代码:
/*list_array.c*/
#include <stdio.h>//printf
#include <stdlib.h>//malloc
#define MAXSIZE 2000
#define TRUE 1
#define FALSE 0
#define ERROR -1
typedef int BOOL;
typedef int Elementype;
typedef int Position;
typedef struct LNode* List;
//数组实现链表, 定义的数据结构
struct LNode{
Elementype Data[MAXSIZE];
Position Last;
};
Position Length(List L);
/*init*/
List MakeEmpty()
{
List L;
L = (List)malloc(sizeof(struct LNode));
L->Last = -1;
return L;
}
/* 查找 */
Position Find(List L, Elementype X)
{
Position i = 0;
while( i <= L->Last && L->Data[i] != X)
i++;
if( i > L->Last){
return ERROR; //如果没有找到,返回错误信息
}else{
return i;//找到后返回的是存储位置
}
}
BOOL Insert(List L, Elementype X, Position P)
{
/*在L的指定位置P前插入一个新元素X*/
Position i;
if(L->Last == MAXSIZE -1)
{
/*表空间已满,不能插入*/
printf("表满");
return FALSE;
}
if( P < 0 || P > L->Last + 1){
//检查插入位置时候合法
printf("位置不合法");
return FALSE;
}
for( i = L->Last; i >= P; i--)
L->Data[i+1] = L->Data[i]; //将位置P以及以后位置往后移动
L->Data[P] = X;//新元素插入
L->Last++;//Last 仍指向最后一个元素
return TRUE;
}
BOOL Delete(List L, Position P)
{
//从L 中删除指定位置P的元素
Position i;
if ( P < 0 || P > L->Last){
//检查空表集删除位置的合法性
printf("位置%d不存在元素",P);
return FALSE;
}
for( i = P + 1; i <= L->Last; i++)
L->Data[i - 1] = L->Data[i];//将位置P+1及以后的位置往前移
L->Last--;//last 指向最后一个元素
return TRUE;
}
void PrintList(List L)
{
Position i;
for(i = 0; i < Length(L); i++)
printf("%d ", L->Data[i]);
printf("\n");
}
Position Length(List L)
{
return L->Last + 1;
}
Elementype getElement(List L, Position P)
{
return L->Data[P];
}
int main()
{
List list;
list = MakeEmpty();
Position index = 0;
for(int i = 10; i >= 0; i--)
{
if(Insert(list,i,index)){
printf(" insert success\n");
}else{
printf(" insert failed\n");
}
index++;
}
PrintList(list);
printf("this list length : %d\n", Length(list));
printf("the positon 2 is : %d \n", getElement(list, 10));
return 0;
}
编译运行:
gcc list_array.c
./a.exe
打印结果:
insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
10 9 8 7 6 5 4 3 2 1 0
this list length : 11
the positon 2 is : 0
——————————线性表的顺序存储——————————————————
DataStructure之线性表以及其实现
原文:https://www.cnblogs.com/Davirain/p/11711289.html


