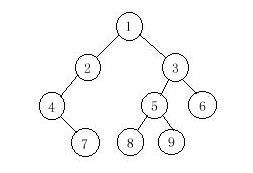
9 1 2 4 7 3 5 8 9 6 4 7 2 1 8 5 9 3 6
7 4 2 8 9 5 6 3 1今天刷二叉树专题,搞了半天终于对重建有了一点认识,首先说一下由先序和中序重建二叉树,大体思路是大概是这样的:因为先序(pre)的第一个字母肯定是根节点,所以要在中序(ins)序列中找到根节点的位置k,然后递归重建根节点的左子树和右子树。此时要把左子树和右子树当成根节点,然后表示出它们的位置,左子树很好说,pre+1就是它的位置,对于右子树来说,pre+k+1为它的位置,如图 对于由中序和后序重建,思路跟上面大体一样,具体写法有点差别,这个就要在中序序列中找到后序的最后一个字母(即根节点),然后递归重建左子树和右子树,依旧是把左子树和右子树当成根节点,左子树的位置为pos+k-1,但传的参数应该是pos (因为我们要找的字母是pos[n-1]),而右子树的位置在后序的倒数第二个字母,传参数为pos+k,(不是pos+k+1,想明白这个就算真明白了)
对于由中序和后序重建,思路跟上面大体一样,具体写法有点差别,这个就要在中序序列中找到后序的最后一个字母(即根节点),然后递归重建左子树和右子树,依旧是把左子树和右子树当成根节点,左子树的位置为pos+k-1,但传的参数应该是pos (因为我们要找的字母是pos[n-1]),而右子树的位置在后序的倒数第二个字母,传参数为pos+k,(不是pos+k+1,想明白这个就算真明白了) 另为这篇没写由后序和中序重建的代码,以前写过,在这点击打开链接
另为这篇没写由后序和中序重建的代码,以前写过,在这点击打开链接#include <cstdio> #include <iostream> #include <algorithm> #include <cstring> #include <cctype> #include <cmath> #include <cstdlib> #include <vector> #include <queue> #include <set> #include <map> #include <list> using namespace std; const int INF=1<<27; const int maxn=5100; typedef struct node { int data; node *l,*r; }*T; void rbuild(T &root,int *pre,int *ins,int n) { if(n<=0) root=NULL; else { root=new node; int k=find(ins,ins+n,pre[0])-ins; root->data=pre[0]; rbuild(root->l,pre+1,ins,k); rbuild(root->r,pre+k+1,ins+k+1,n-k-1); } } int ans[maxn],p; void last(T root) { if(root) { last(root->l); last(root->r); ans[p++]=root->data; } } int main() { int n,i; while(cin>>n){ T root;int pre[maxn],ins[maxn]; for(i=0;i<n;i++) cin>>pre[i]; for(i=0;i<n;i++) cin>>ins[i]; rbuild(root,pre,ins,n); p=0; last(root); for(i=0;i<p;i++) if(i!=p-1) cout<<ans[i]<<" "; else cout<<ans[i]<<endl; } return 0; }
HDU 1710-Binary Tree Traversals(重建二叉树),布布扣,bubuko.com
HDU 1710-Binary Tree Traversals(重建二叉树)
原文:http://blog.csdn.net/qq_16255321/article/details/38729307