P2996

传送门

题意：

给你一棵树，每一条边上最多选一个点，问你选的点数.

我的思想：

一开始我是想用黑白点染色的思想来做，就是每一条边都选择一个点.

可以跑两边一遍在意的时候染成黑，第二遍染成白,取一个最大值.

就可以得到\(30\)分的高分.

#include <bits/stdc++.h>
#define N 100010
#define M 1010
#define _ 0

using namespace std;
int n, tot, ans, add_edge, color[N], head[N];
struct node {
    int next, to;
}edge[N];

int read() {
    int s = 0, f = 0; char ch = getchar();
    while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
    return f ? -s : s;
}

void add(int from, int to) {
    edge[++add_edge].next = head[from];
    edge[add_edge].to = to;
    head[from] = add_edge;
}

void dfs(int x, int fx) {
    if (color[fx] == 0) {
        color[x] = 1;
        tot++;
    }
    for (int i = head[x]; i; i = edge[i].next) {
        int to = edge[i].to;
        if (to == fx) continue;
        dfs(to, x);
    }
}

int main() {
    n = read();
    int point;
    for (int i = 1, x, y; i < n; i++) {
        x = read(), y = read();
        add(x, y), add(y, x);
        point = x;
    }
    dfs(point, 0);
    ans = max(ans, tot);
    memset(color, 0, sizeof (color));
    tot = 0, color[0] = 1;
    dfs(point, 0);
    cout << max(ans, tot);
}

很明显这样做是错误的.来看这样一组样例.

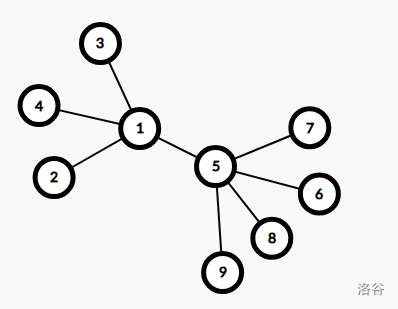
按照上述方法跑出来就是\(5\)，显然答案是\(7\).然后我就是这样被学长\(hack\)了.

然后就问了学长树形\(DP\).

正确思路:

我们设\(dp[i][1/0]\)来表示\(i\)与\(i\)的子树在\(i\)，选还是不选，时的最大权值.

然后又因为在\(dp[i][1]\)时他的子节点不能选\(dp[to][1]\).

在\(dp[i][0]\)时都可以选.我们就可以得到这样的转移方程(用\(to\)来表示\(i\)的子节点)：

\[dp[x][0] += max(dp[to][1], dp[to][0]);\]
\[ dp[x][1] += dp[to][0]; \]

然后就做完了.

code :

#include <bits/stdc++.h>
#define N 100010
#define M 50010
#define _ 0

using namespace std;
int n, add_edge, head[N];
int dp[M][2];
struct node {
    int next, to;
}edge[N];

int read() {
    int s = 0, f = 0; char ch = getchar();
    while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
    return f ? -s : s;
}

void add(int from, int to) {
    edge[++add_edge].next = head[from];
    edge[add_edge].to = to;
    head[from] = add_edge;
}

void dfs(int x, int fx) {
    dp[x][1] = 1;
    for (int i = head[x]; i; i = edge[i].next) {
        int to = edge[i].to;
        if (to == fx) continue;
        dfs(to, x);
        dp[x][0] += max(dp[to][1], dp[to][0]);
        dp[x][1] += dp[to][0];
    }
}

int main() {
    n = read();
    for (int i = 1, x, y; i < n; i++) {
        x = read(), y = read();
        add(x, y), add(y, x);
    }
    dfs(1, 0); 
    cout << max(dp[1][0], dp[1][1]);
}

洛谷 P2996 [USACO10NOV]拜访奶牛Visiting Cows

原文：https://www.cnblogs.com/zzz-hhh/p/11714431.html