有如下方程组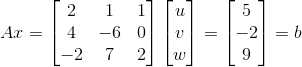 
，当矩阵 A 各列向量互不相关时， 方程组有位移解，可以使用消元法求解，具体如下：
使用消元矩阵将 A 变成上三角矩阵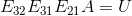 
，
，
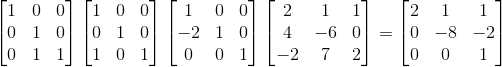使用消元矩阵作用于向量 b，得到向量 c，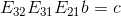
，
，
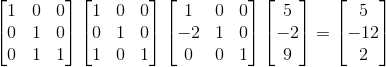Ax=b 消元后变为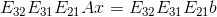 
，即 
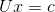， 由于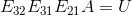 
为上三角矩阵， 使用回带法即可求解方程组。
对矩阵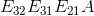 
做如下运算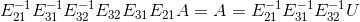 
。在消元过程中，已知 
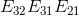，如何求解 
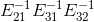呢？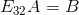
表示将矩阵A的第二行乘以 1 再加上矩阵A的第三行得到矩阵B的第三行，矩阵B的第一二行于矩阵A的第一二行保持一致。根据语义，
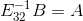表示将矩阵B的第二行乘以 -1 再加上矩阵B的第三行得到矩阵A的第三行，矩阵A的第一二行于矩阵B的第一二行保持一致。
，
，
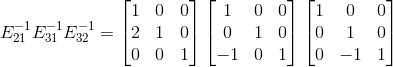通过以上观察，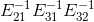
仅需将对角线下元素相加即可得到，
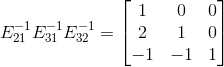，在矩阵消元过程中，对消元系数取反，然后放在相应的位置即构成了 
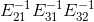，也就是 L 。同时，消元法记录下了 U，则有 Ux=c, b=Lc。
由于 L 为下三角矩阵，根据 Lc=b, 可求解 c；U 为上三角矩阵， 根据 Ux=c 可求解 x。
在消元过程中，如果遇到主元位置上为 0 情况时，需要使用行变换矩阵使消元过程得以继续，PAx=Pb，P为行变换矩阵，记录矩阵 L，U，P，可实现LU分解，过程如下：
有方程组 
，对矩阵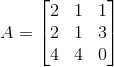 
进行LU分解：
1）
， 
，
；
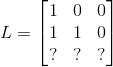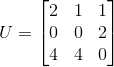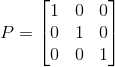2）
，
，
；
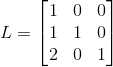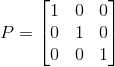3）由于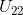 
为 0，需要交换2，3行，则有：
， 
，
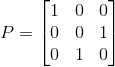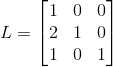，交换L矩阵中小于第二列下变换因子位置，即交换 
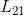与 
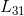元素位置；
4）由于 Lc=Pb, 可计算出 c:
， 
；
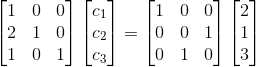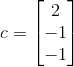5）由于 Ux=c，可计算出 x:
，
。
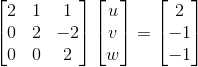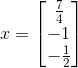参考资料 Linear Algebra And Its Applications Gilbert Strang
原文：https://www.cnblogs.com/luofeiju/p/11714224.html