一、实践题目
这一次由于我只做出了第一道实践题,即数字三角形问题,所以没的选择,只能写这道题的实践报告了。
二、问题描述
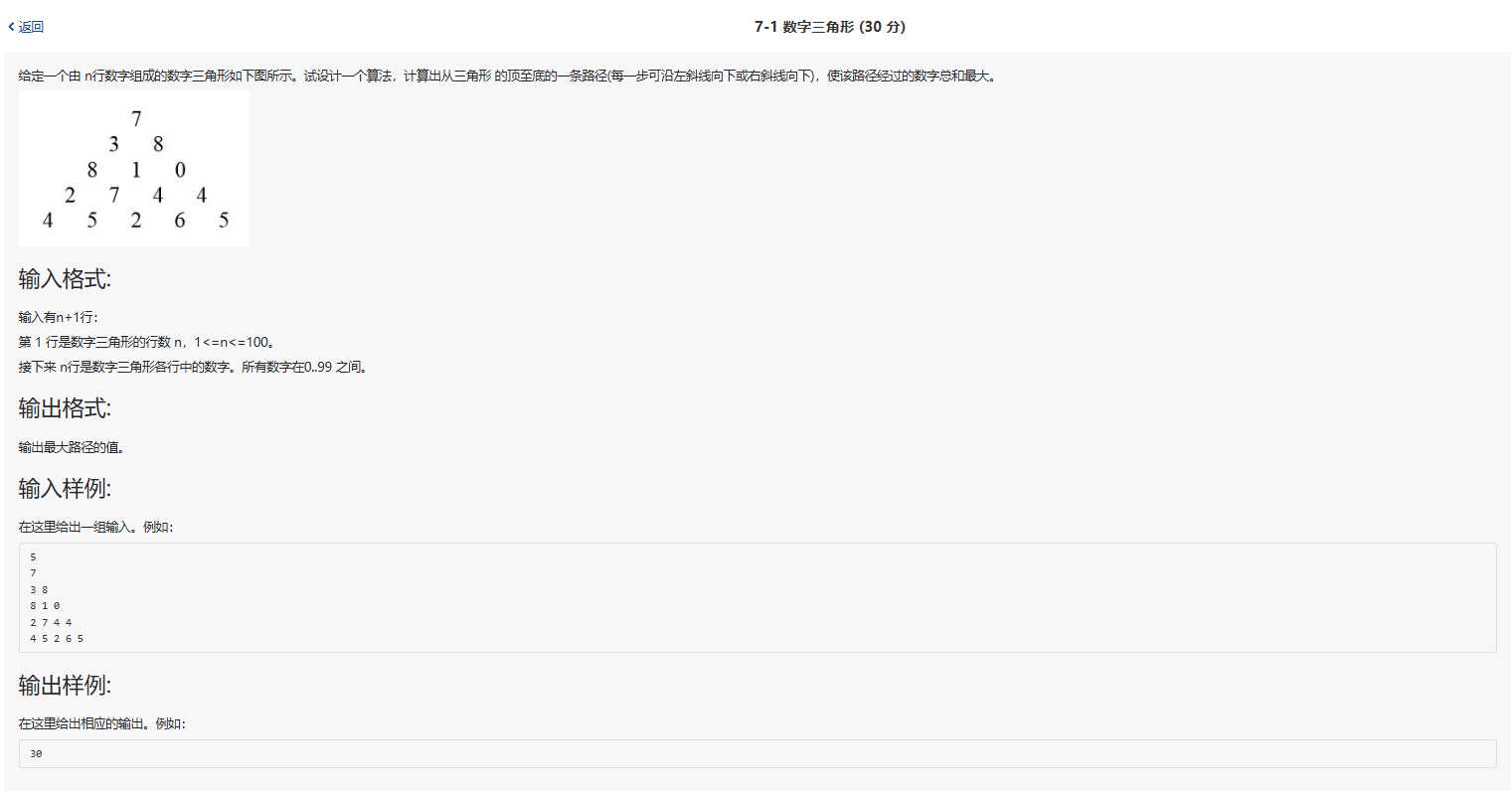
题目里虽然没有说,但是老师要求使用第三章的动态规划算法,同时还要用上“备忘录”,不然的话提交会出现运行超时的错误。
三、算法描述
程序的大致思路就是通过一层层的递归,要求n行数字三角形的最大路径和,就要先求出(n-1)行数字三角形的最大路径和,依次类推。
其递归方程为: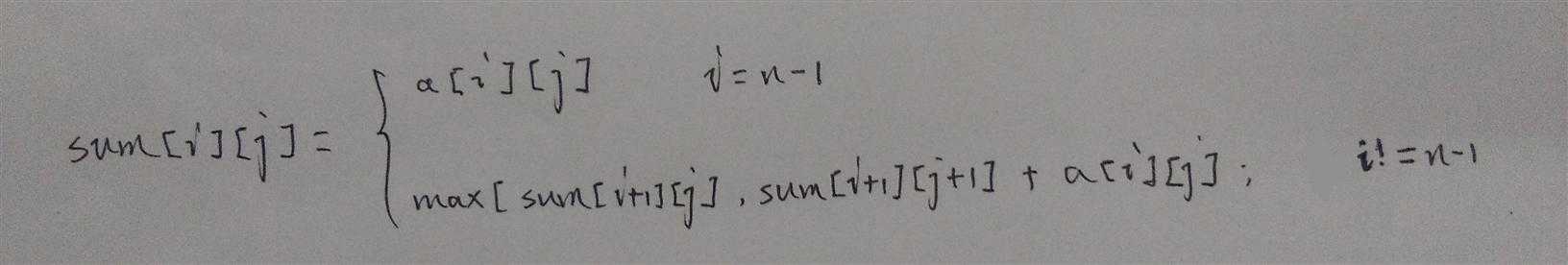 源代码为:
源代码为:
1 #include<iostream> 2 using namespace std; 3 4 int sum(int i, int j, int n, int a[100][100], int num[100][100]) 5 { 6 if (num[i][j] != -1) 7 return num[i][j]; 8 //若该位置的值不为-1,则说明已经保存有数据,直接返回结果,节省计算的时间 9 if (i == n - 1) 10 num[i][j] = a[i][j]; 11 //已经递归到最深一层,直接把数字三角形对应的值存入备忘录 12 else 13 { 14 int x = sum(i + 1, j, n, a, num);//求其左下方的最优子结构 15 int y = sum(i + 1, j + 1, n, a, num);//求其右下方的最优子结构 16 num[i][j] = (x >= y ? x : y) + a[i][j]; 17 //比较x、y的值,将最优解存入备忘录 18 } 19 return num[i][j]; 20 } 21 22 int main() 23 { 24 int a[100][100];//定义一个二维数组存放数字三角形 25 int n; 26 cin >> n; 27 for (int i = 0;i < n;i++) 28 for (int j = 0;j < i + 1;j++) 29 cin >> a[i][j]; 30 int num[100][100];//定义一个备忘录存放最优子结构 31 for (int i = 0;i < n;i++) 32 for (int j = 0;j < i + 1;j++) 33 num[i][j] = -1;//对备忘录进行初始化 34 int value = sum(0, 0, n, a, num); 35 cout << value; 36 system("pause"); 37 return 0; 38 }
四、算法时间及空间复杂度的分析
时间复杂度:
T(n)= n + (n-1) + (n-2) + … + 1 = n(n-1)/2 = n^2
在第n行,程执行n次将数据存入备忘录,(n-1)层每个数字经过一次比较,最后执行(n-1)次将数据存入备忘录,依次类推,得出最后时间复杂度为n^2。
空间复杂度:
程序需要用到的空间,是一个备忘录数组,数组大小为n * n,即空间复杂度O(n)= n^2。
五、心得体会
由于对动态规划算法的不熟悉,所以在这道题上花费了太多时间,以至于没有时间去做其他题。此外,备忘录方法真的可以很大程度上节省程序运行所需的时间,我一开始打的代码因为没有用备忘录,提交上去后就直接超时了。
孰能生巧,这类新算法、新思想还是要多打代码才能够熟练使用啊。
原文:https://www.cnblogs.com/Raido/p/11715896.html