网格计数

也许更好的阅读体验

\(\mathcal{Description}\)
一个\(n*m\)的网格,问有多少对从\(\left(1,1\right)\)出发到\(\left(n,m\right)\)路径满足没有交点
\(T\)组询问,\(T\leq 5\times 10^5,n,m\leq 10^6\)
\(\mathcal{Solution}\)
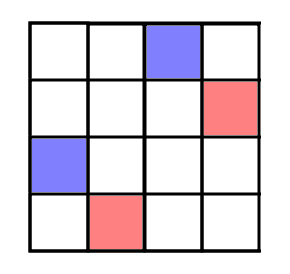
如图,要求没有交点,所以实际上问的是以蓝色/红色为起点,到各自终点且没有交点的路径对
考虑容斥,即所有的路径对数减去不合法的路径对数

我们画一对有交点的路径对

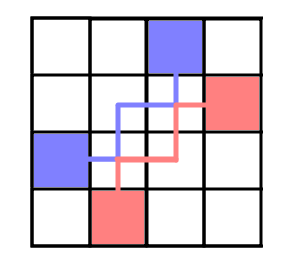
我们把其最后一个交点的路径交换

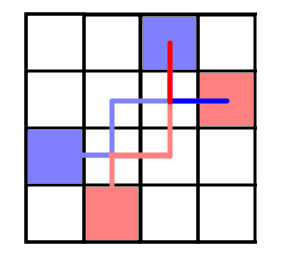
发现,所有的有交点的路径都唯一对应一种从蓝色/红色走到另外一种颜色的终点的方案
照上述算方案容斥即可
计算方案则考虑要往右\(n\)次,往上\(m\)次,则有\(\begin{pmatrix}n+m\\n\end{pmatrix}\)种方案
故最终答案就是,先令\(n=n-2,m=m-2\),即要往右/往上的次数
\(ans=\begin{pmatrix}n+m\\n\end{pmatrix}^2-\begin{pmatrix}n+m\\n-1\end{pmatrix}\begin{pmatrix}n+m\\n+1\end{pmatrix}\)

\(\mathcal{Code}\)

/*******************************
Author:Morning_Glory
LANG:C++
Created Time:2019年10月21日 星期一 09时50分11秒
*******************************/
#include <cstdio>
#include <fstream>
#define ll long long
using namespace std;
const int maxn = 2000006;
const int lim = 2000000;
const int mod = 998244353;
//{{{cin
struct IO{
    template<typename T>
    IO & operator>>(T&res){
        res=0;
        bool flag=false;
        char ch;
        while((ch=getchar())>'9'||ch<'0')   flag|=ch=='-';
        while(ch>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch^'0'),ch=getchar();
        if (flag)   res=~res+1;
        return *this;
    }
}cin;
//}}}
int T,n,m;
int fac[maxn],inv[maxn],ifac[maxn];
int C (int n,int m){    return 1ll*fac[n]*ifac[n-m]%mod*ifac[m]%mod;}
int main()
{
    fac[0]=ifac[0]=inv[1]=1;
    for (int i=2;i<=lim;++i)    inv[i]=(-1ll*mod/i*inv[mod%i]%mod+mod)%mod;
    for (int i=1;i<=lim;++i)    fac[i]=1ll*fac[i-1]*i%mod,ifac[i]=1ll*ifac[i-1]*inv[i]%mod;
    cin>>T;
    while (T--){
        cin>>n>>m;
        n-=2,m-=2;
        printf("%d\n",(1ll*C(n+m,n)*C(n+m,n)%mod-1ll*C(n+m,n-1)*C(n+m,n+1)%mod+mod)%mod);
    }
    return 0;
}

如有哪里讲得不是很明白或是有错误，欢迎指正
如您喜欢的话不妨点个赞收藏一下吧

网格计数

原文：https://www.cnblogs.com/Morning-Glory/p/11722333.html