传送门:https://www.luogu.org/problem/P1063
从今以后区间dp应该没问题了
很容易想到和石子合并一样的操作,首先破环为链,将环断开变成两倍,题中的例子就会变成这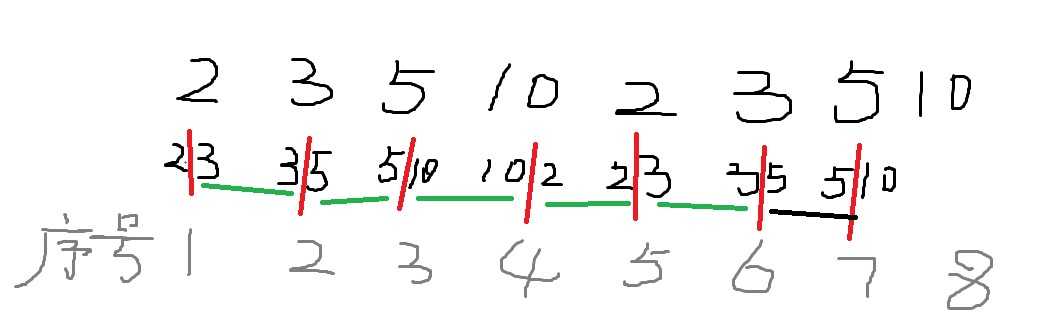
之后设dp[ l ][ r ],分别枚举起点 i 和长度 k 以及分割点 x
由此可得状态转移方程:dp[l][r]=max(dp[l][r],dp[l][i]+dp[i+1][r]+num[l]*num[i+1]*num[r+1])
代码如下
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n; 4 int num[109]; 5 long long ans; 6 long long dp[209][209]; 7 inline int kd() 8 { 9 int x=0,f=1;char ch=getchar(); 10 while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} 11 while(ch>=‘0‘&&ch<=‘9‘){x=x*10+(ch^48);ch=getchar();} 12 return x*f; 13 } 14 int main() 15 { 16 n=kd(); 17 for(int i=1;i<=n;i++) 18 { 19 num[i]=kd(); 20 num[i+n]=num[i];//破环为链 21 } 22 for(int k=2;k<=n;k++)//枚举合并长度 23 { 24 for(int l=1;l+k-1/*终点小于长度*/<=2*n;l++)//枚举起点 25 { 26 int r=l+k-1;//算出终点 27 for(int i=l;i<=r-1;i++)//枚举分割点 28 { 29 dp[l][r]=max(dp[l][r],dp[l][i]+dp[i+1][r]/*两段原来的最大值*/+num[l]*num[i+1]*num[r+1]/*合并产生的值*/); 30 } 31 } 32 } 33 for(int i=1;i<=n;i++) 34 { 35 ans=max(ans,dp[i][i+n-1]);//枚举出最大值 36 } 37 cout<<ans; 38 }
原文:https://www.cnblogs.com/1129-tangqiyuan/p/11728810.html