堆排序

什么是堆？

堆是具有以下性质的完全二叉树：

• 每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆
• 或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

如下图所示:

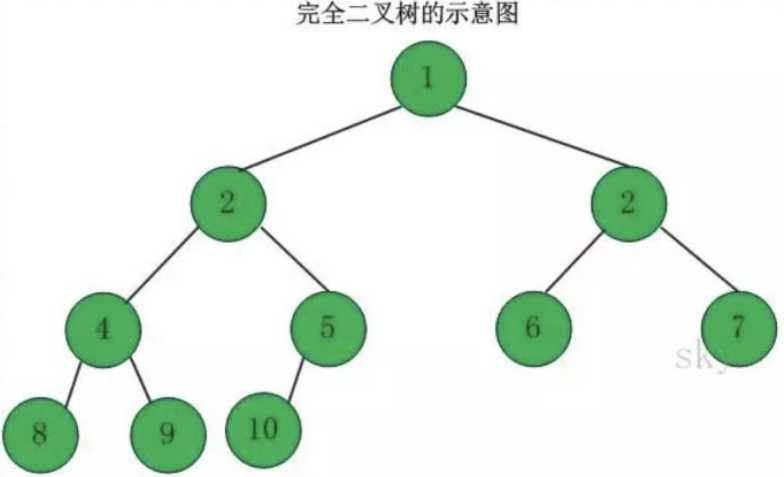
那么话又说回来了，什么是完全二叉树呢？

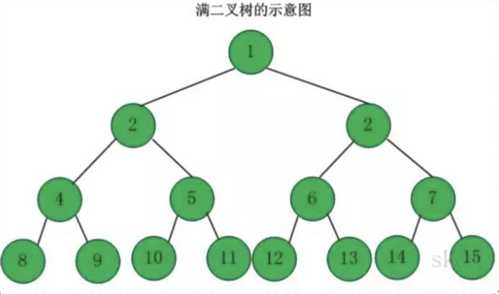
要想知道什么是完全二叉树，首先得知道什么满二叉树。

• 满二叉树:高度为h，并且由 2^h-1个结点的二叉树，被称为满二叉树，其实不难看出，满二叉树的结点的度要么为0（叶子结点），要么为2（非叶子结点）

• 完全二叉树:一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
  特点:叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

堆与一维数组的映射关系

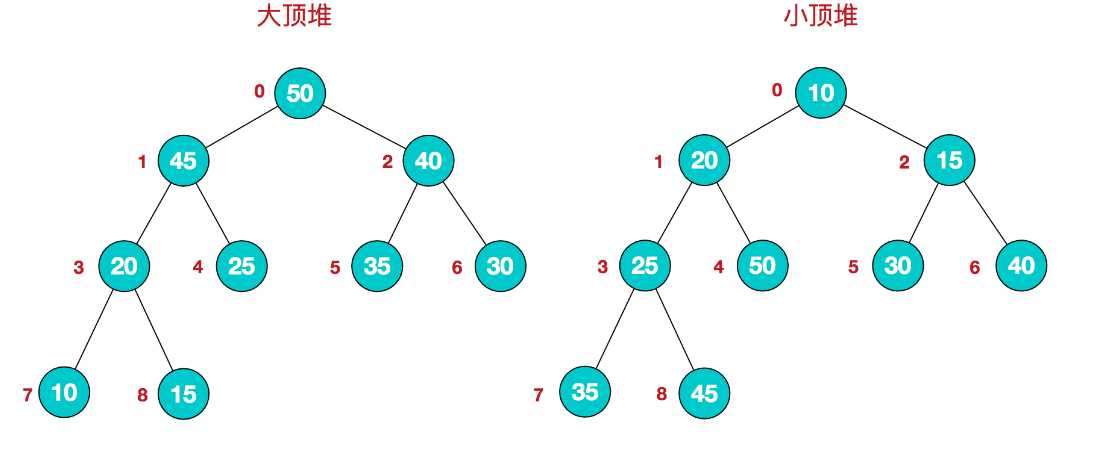
同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

简单的说对于二叉树中的任意一个节点，假设它的下标为i，那么它左孩子的节点在数组中的下标就是2i+1,而其右孩子节点的下标就是2i+2

因此对于大顶堆来说满足一下的条件:

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

对于小顶堆来说满足

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆排序的思想

• 利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。
• 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
• 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

堆排序的动画演示

堆排序的代码实现

package sort;

import java.util.Arrays;

public class HeapSort {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] arr= {4,6,8,5,9};
        System.out.println(Arrays.toString(arr));
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }
    
    //堆排序
    public static void heapSort(int[] arr)
    {
        //将无序的数组构造成一个堆，根据升序或者降序选择大顶堆或者小顶堆
        for(int i=arr.length/2-1;i>=0;i--)
        {
            adjustHeap(arr, i, arr.length);
        }
        //交换
        for(int j=arr.length-1;j>0;j--)
        {
            int temp=arr[j];
            arr[j]=arr[0];
            arr[0]=temp;
            adjustHeap(arr, 0, j);
        }
    }
    
    //将数组（二叉树），调整成一个大顶堆
    /*
       * 完成将以i对应的非叶子节点调整成大顶堆
     * 
     * i表示非叶子节点在数组中的索引
     * len代表对多少个元素进行调整，length在不断的减少
     * 
     */
    public static void adjustHeap(int[] arr,int i,int length)
    {
        int temp=arr[i];//取出当前元素的值，保存为临时变量
        //开始调整
        //k指向的i这个节点的左子节点
        for(int k=i*2+1;k<length;k=k*2+1)
        {
            if(arr[k]<arr[k+1]&&k+1<length)//左子节点小于右子节点的值
            {
                k++;//k指向右子节点
            }
            if(arr[k]>temp)//子节点大于父节点
            {
                arr[i]=arr[k];//把较大的值赋值给当前的节点
                i=k;//i指向k，继续循环比价
            }
            else
            {
                break;//因为是从下至上的比较
            }
            
        }
        //当for循环结束之后已经将以i为父节点的最大值放在i的位置，局部大顶堆
        arr[i]=temp;//放到调整后的位置
    }

}

堆排序的特点

• 堆排序的平均时间复杂度为{nlogn}
• 堆排序的空间复杂度是{O(n)}
• 不稳定的排序算法

堆排序

原文：https://www.cnblogs.com/mengxiaoleng/p/11729131.html