实验表明,RNN 在几乎所有的序列问题上都有良好表现,包括语音/文本识别、机器翻译、手写体识别、序列数据分析(预测)等。
在实际应用中,RNN 在内部设计上存在一个严重的问题:由于网络一次只能处理一个时间步长,后一步必须等前一步处理完才能进行运算。这意味着 RNN 不能像 CNN 那样进行大规模并行处理,特别是在 RNN/LSTM 对文本进行双向处理时。这也意味着 RNN 极度地计算密集,因为在整个任务运行完成之前,必须保存所有的中间结果。
CNN 在处理图像时,将图像看作一个二维的“块”(m*n 的矩阵)。迁移到时间序列上,就可以将序列看作一个一维对象(1*n 的向量)。通过多层网络结构,可以获得足够大的感受野。这种做法会让 CNN 非常深,但是得益于大规模并行处理的优势,无论网络多深,都可以进行并行处理,节省大量时间。这就是 TCN 的基本思想。
TCN 模型以 CNN 模型为基础,并做了如下改进:
下面将分别介绍 CNN 的扩展技术。
因为要处理序列问题(时序性),就必须使用新的 CNN 模型,这就是因果卷积。序列问题可以转化为:根据 去预测
。下面给出因果卷积的定义,滤波器
,序列
,在
处的因果卷积为:
。下图为一个因果卷积的实例,假设输入层最后两个节点分别为
,第一层隐藏层的最后一个节点为
,滤波器
,根据公式有
。
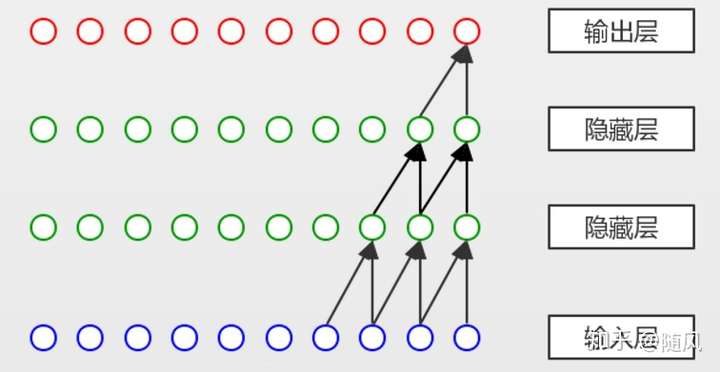
因果卷积有两个特点:
标准的 CNN 通过增加 pooling 层来获得更大的感受野,而经过 pooling 层后肯定存在信息损失的问题。空洞卷积是在标准的卷积里注入空洞,以此来增加感受野。空洞卷积多了一个超参数 dilation rate,指的是 kernel 的间隔数量(标准的 CNN 中 dilatation rate 等于 1)。空洞的好处是不做 pooling 损失信息的情况下,增加了感受野,让每个卷积输出都包含较大范围的信息。下图展示了标准 CNN (左)和 Dilated Convolution (右),右图中的 dilatation rate 等于 2 。
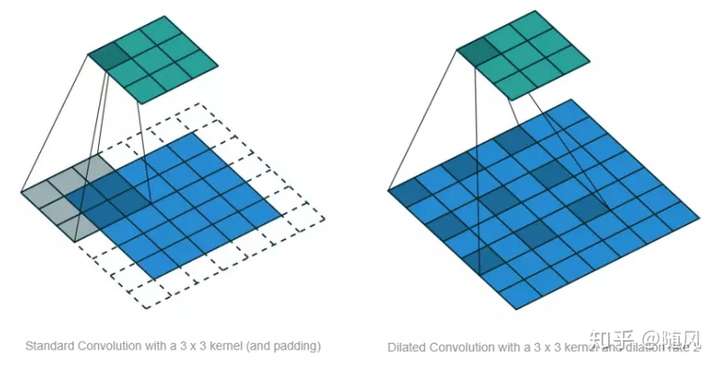
下面给出空洞卷积的定义,滤波器 ,序列
,在
处的 dilatation rate 等于 d 的空洞卷积为:
,下图为一个空洞卷积的实例,假设第一层隐藏层最后五个节点分别为
,第二层隐藏层的最后一个节点为
,滤波器
,根据公式有
。
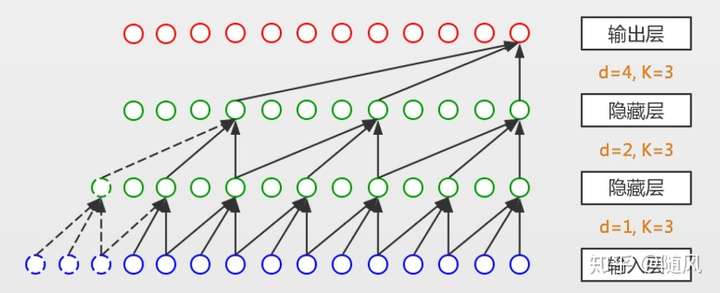
空洞卷积的感受野大小为 ,所以增大
或
都可以增加感受野。在实践中,通常随网络层数增加,
以
的指数增长,例如上图中
依次为
。
CNN 能够提取 low/mid/high-level 的特征,网络的层数越多,意味着能够提取到不同 level的特征越丰富。并且,越深的网络提取的特征越抽象,越具有语义信息。
如果简单地增加深度,会导致梯度消失或梯度爆炸。对于该问题的解决方法是权重参数初始化和采用正则化层(Batch Normalization),这样可以训练几十层的网络。解决了梯度问题,还会出现另一个问题:网络退化问题。随着网络层数的增加,在训练集上的准确率趋于饱和甚至下降了。注意这不是过拟合问题,因为过拟合会在训练集上表现的更好。下图是一个网络退化的例子,20 层的网络比 56 层的网络表现更好。
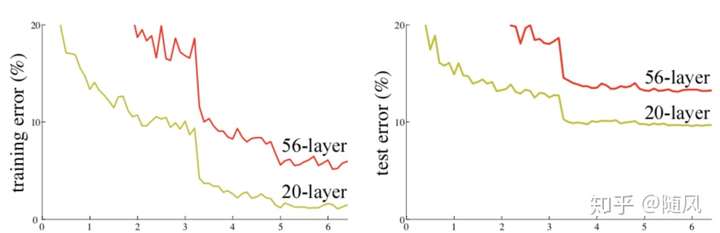
理论上 56 层网络的解空间包括了 20 层网络的解空间,因此 56 层网络的表现应该大于等于20 层网络。但是从训练结果来看,56 层网络无论是训练误差还是测试误差都大于 20 层网络(这也说明了为什么不是过拟合现象,因为 56 层网络本身的训练误差都没有降下去)。这是因为虽然 56 层网络的解空间包含了 20 层网络的解空间,但是我们在训练中用的是随机梯度下降策略,往往得到的不是全局最优解,而是局部最优解。显然 56 层网络的解空间更加的复杂,所以导致使用随机梯度下降无法得到最优解。
假设已经有了一个最优的网络结构,是 18 层。当我们设计网络结构时,我们并不知道具体多少层的网络拥有最优的网络结构,假设设计了 34 层的网络结构。那么多出来的 16 层其实是冗余的,我们希望训练网络的过程中,模型能够自己训练这 16 层为恒等映射,也就是经过这16 层时的输入与输出完全一样。但是往往模型很难将这 16 层恒等映射的参数学习正确,这样的网络一定比最优的 18 层网络表现差,这就是随着网络加深,模型退化的原因。
因此解决网络退化的问题,就是解决如何让网络的冗余层产生恒等映射(深层网络等价于一个浅层网络)。通常情况下,让网络的某一层学习恒等映射函数 比较困难,但是如果我们把网络设计为
,我们就可以将学习恒等映射函数转换为学习一个残差函数
,只要
,就构成了一个恒等映射
。在参数初始化的时候,一般权重参数都比较小,非常适合学习
,因此拟合残差会更加容易,这就是残差网络的思想。
下图为残差模块的结构,该模块提供了两种选择方式,也就是 identity mapping(即 ,右侧“弯弯的线",称为 shortcut 连接) 和 residual mapping(即
),如果网络已经到达最优,继续加深网络,residual mapping 将被 push 为 0,只剩下 identity mapping,这样理论上网络一直处于最优状态了,网络的性能也就不会随着深度增加而降低了。
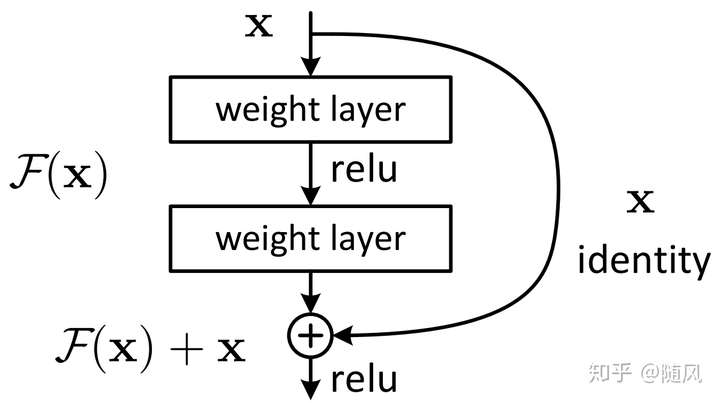
这种残差模块结构可以通过前向神经网络 + shortcut 连接实现。而且 shortcut 连接相当于简单执行了同等映射,不会产生额外的参数,也不会增加计算复杂度,整个网络依旧可以通过端到端的反向传播训练。
上图中残差模块包含两层网络。实验证明,残差模块往往需要两层以上,单单一层的残差模块 并不能起到提升作用。shortcut 有两种连接方式:
(1)identity mapping 同等维度的映射( 与
维度相同):
(2)identity mapping 不同维度的映射( 与
维度不同):
以上是基于全连接层的表示,实际上残差模块可以用于卷积层。加法变为对应 channel 间的两个 feature map 逐元素相加。
设计 CNN 网络的规则:
(1)对于输出 feature map 大小相同的层,有相同数量的 filters,即 channel 数相同;
(2)当 feature map 大小减半时(池化),filters 数量翻倍;
对于残差网络,维度匹配的 shortcut 连接为实线,反之为虚线。维度不匹配时,同等映射(identity mapping)有两种可选方案:
(1)直接通过 zero padding 来增加 channels(采用 zero feature map 补充)。
(2)增加 filters,直接改变 1x1 卷积的 filters 数目,这样会增加参数。
在实际中更多采用 zero feature map 补充的方式。
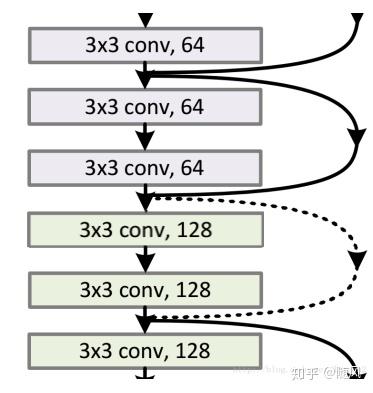
在残差网络中,有很多残差模块,下图是一个残差网络。每个残差模块包含两层,相同维度残差模块之间采用实线连接,不同维度残差模块之间采用虚线连接。网络的 2、3 层执行 3x3x64 的卷积,他们的 channel 个数相同,所以采用计算: ;网络的 4、5 层执行 3x3x128 的卷积,与第 3 层的 channel 个数不同 (64 和 128),所以采用计算方式:
。其中
是卷积操作(用 128 个 3x3x64 的 filter),用来调整 x 的 channel 个数。
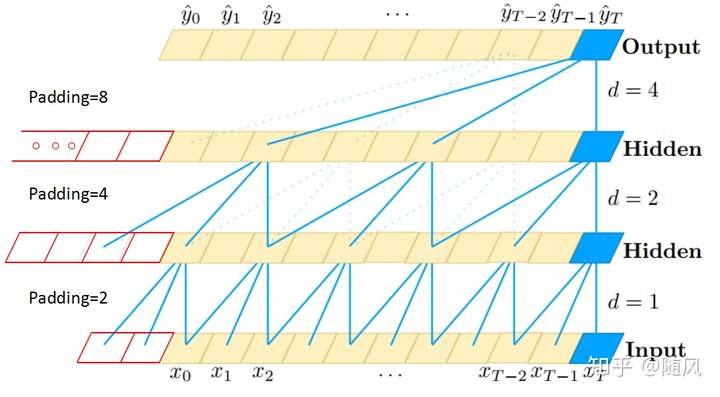
因为研究对象是时间序列,TCN 采用一维的卷积网络。下图是 TCN 架构中的因果卷积与空洞卷积,可以看到每一层 时刻的值只依赖于上一层
时刻的值,体现了因果卷积的特性;而每一层对上一层信息的提取,都是跳跃式的,且逐层 dilated rate 以 2 的指数增长,体现了空洞卷积的特性。由于采用了空洞卷积,因此每一层都要做 padding(通常情况下补 0),padding 的大小为
。
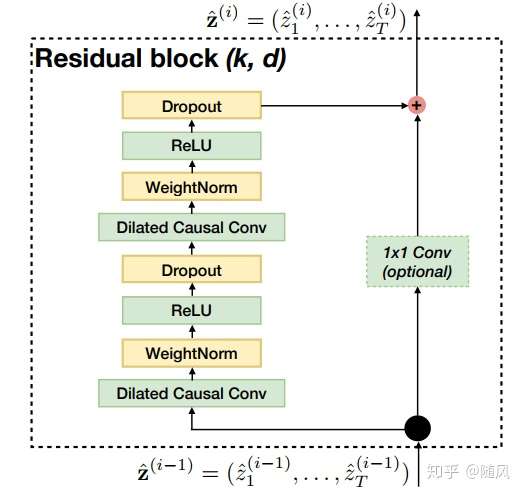
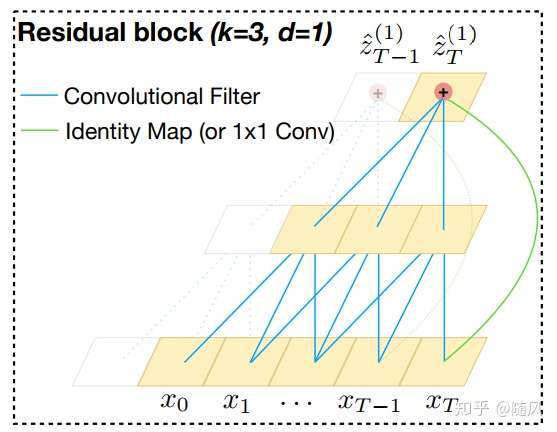
下图是 TCN 架构中的残差模块,输入经历空洞卷积、权重归一化、激活函数、Dropout(两轮),作为残差函数 ;输入经历 1x1 卷积 filters,作为 shortcut 连接的
。
下图是 TCN 的一个例子,当 时,空洞卷积退化为普通卷积。
转自知乎:https://zhuanlan.zhihu.com/p/69919158
原文:https://www.cnblogs.com/USTC-ZCC/p/11734436.html